10. Area and Average Value

c. Area as a \(y\)-Integral

On the previous pages, we computed the area of a region whose edges were specified by giving \(y\) as a function of \(x\). We now look at regions whose edges are specified by giving \(x\) as a function of \(y\). Everything is the same as previously, except we need to turn our heads sidewise. Animated happy face telling students to turn their head to the right.

Find the area to the left of a function \(x=f(y)\) and to the right of a function \(x=g(y)\) between \(y=c\) and \(y=d\).

This time divide the region into \(n\) horizontal rectangles each of height \(\Delta y=\dfrac{d-c}{n}\) and width \(f(y_i^*)-g(y_i^*)\) where \(y_i^*\) is a point in the \(i^\text{th}\) interval.

The area is then obtained by adding up the areas of the rectangles and taking the limit as the number of rectangles becomes large, (\(n\rightarrow\infty\)): \[ A=\lim_{n\rightarrow\infty}\sum_{i=1}^n [f(y_i^*)-g(y_i^*)]\Delta y \] This limit of the sum is recognized as the integral \[ A=\int_c^d [f(y)-g(y)]\,dy \]

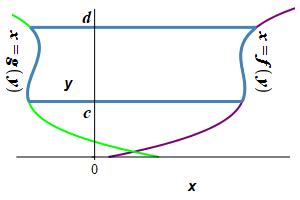
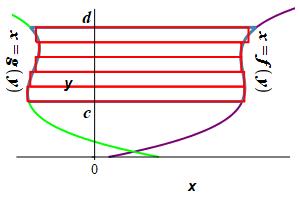
The plot shows two curves with x as a function of y. The left one is decreasing and labeled g of y. The right one is increasing and labeled f of y. There are two blue horizontal lines at y equals c and y equals d which go from g of y to f of y. The plot starts with the same plot as above and adds 4 horizontal lines between c and d, connecting the two functions. These lines brake up the area into 5 small rectangles. 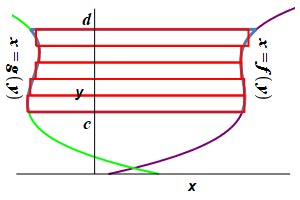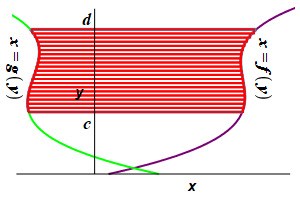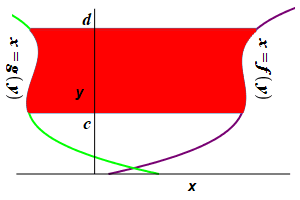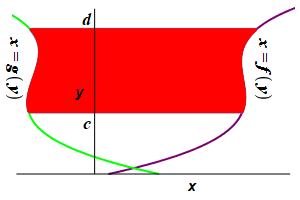This animation starts with the same plot as above, except it adds with more and more horizontal lines, until the region between the functions and between c and d is totally filled in.

The area to the left of a function \(x=f(y)\) and to the right of a function \(x=g(y)\) between \(y=c\) and \(y=d\) is: \[ A=\int_c^d [f(y)-g(y)]\,dy \]

Find the area between the parabolas \(x=2y^2\) and \(x=3+y^2\).

We plot the curves to get an idea of the shape. The curves are both parabolas opening to the right. To find the intersection points, we equate the functions and solve for \(y\): \[\begin{aligned} 2y^2&=3+y^2 \\ y^2&=3 \\ y&=\pm\sqrt{3} \end{aligned}\] Then the area is

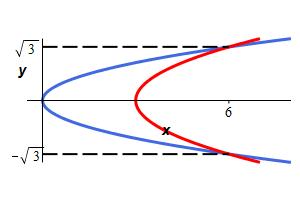
This plot shows two parabola curves opening to the right. They are symmetric about the x axis, with the vertex of the left curve at the origin and the vertex of the right curve at x equals 3. The two curves intersect at y equals plus or minus square root 3, forming a crescent region between the curves.

\[\begin{aligned} A&=\int_{-\sqrt{3}}^{\sqrt{3}} [\text{right}-\text{left}]\,dy =\int_{-\sqrt{3}}^{\sqrt{3}} [(3+y^2)-(2y^2)]\,dy \\ &=\int_{-\sqrt{3}}^{\sqrt{3}} (3-y^2)\,dy =\left[ 3y-\dfrac{y^3}{3}\right]_{y=-\sqrt{3}}^{\sqrt{3}} \\ &=2\left[ 3\sqrt{3}-\dfrac{\sqrt{3}^3}{3}\right] =4\sqrt{3} \end{aligned}\]

Find the area between \(x=y^3+3y^2\) and the \(y\)-axis for \(2 \le y \le 4\).

You don't really need a graph, but here it is:

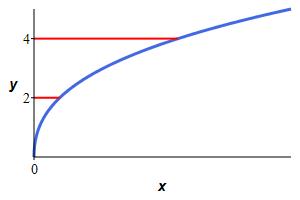
The plot shows the graph of x as a cubic function of y, starting at the origin and increasing to the right. There are two horizontal lines that go from the y axis to the curve, at y equals 2 and at y equals 4.

\(\displaystyle A=\int_2^4 (y^3+3y^2)\,dy=116\)

This is a simple area under a curve but in the \(y\) direction. \[\begin{aligned} A&=\int_2^4 (y^3+3y^2)\,dy =\left[\dfrac{y^4}{4}+y^3\right]_2^4 \\ &=[64+64]-[4+8]=116 \end{aligned}\]

The plot shows the graph of x as a cubic function of y, starting at the origin and increasing to the right. There are two horizontal lines that go from the y axis to the curve, at y equals 2 and at y equals 4.

Find the area between \(x=y^3-y^2\) and \(x=12y\).

Here is the graph of the two curves:

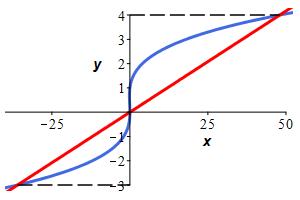
The plot shows the graph of x as a cubic function of y, overall increasing and concave up on the left of the y axis and concave down on the right of the y axis. The plot also shows a line with a positive slope, intersecting the cubic at y equals -3, 0, and 4, forming two regions between two functions.

\(\displaystyle A=\int_{-3}^0 (y^3-y^2-12y)\,dy +\int_0^4 (12y-y^3+y^2)\,dy =\dfrac{937}{12}\)

The cubic is \(0\) at \(y=0\) and \(y=1\) and is positive for \(y \gt 1\). It's graph and the graph of the line are shown. We find the points of intersection by setting the curves equal: \[\begin{aligned} y^3-y^2&=12y \\ y^3-y^2-12y&=0 \\ y(y-4)(y+3)&=0 \end{aligned}\] So, the curves intersect at \(y=-3,0,4\).

The plot shows the graph of x as a cubic function of y, overall increasing and concave up on the left of the y axis and concave down on the right of the y axis. The plot also shows a line with a positive slope, intersecting the cubic at y equals -3, 0, and 4, forming two regions between two functions.

For \(-3 \lt y \lt 0\), the cubic is to the right of the line. (Check \(y=-1\).) For \(0 \lt y \lt 4\), the line is to the right of the cubic. (Check \(y=1\).) So the area is \[\begin{aligned} A&=\int_{-3}^0 (y^3-y^2-12y)\,dy +\int_0^4 (12y-y^3+y^2)\,dy \\ &=\left[\dfrac{y^4}{4}-\dfrac{y^3}{3}-6y^2\right]_{-3}^0 +\left[6y^2-\dfrac{y^4}{4}+\dfrac{y^3}{3}\right]_0^4 \\ &=(0)-\left(\dfrac{81}{4}+9-54\right) +\left(96-64+\dfrac{64}{3}\right)-(0) \\ &=77+\dfrac{-243+256}{12} =\dfrac{937}{12} \end{aligned}\]

You can also practice computing Areas as \(y\)-Integrals by using the following Maplet (requires Maple on the computer where this is executed):

Area of a Region   Rate It

Now look at the problems where \(x\) is a function of \(y\).

© MY Math Apps

Supported in part by NSF Grant #1123255

NSF logo