10. Area and Average Value
b2. Area Between Two Curves - In Pieces
Sometimes the curves intersect more than twice. So you need to do the integral in pieces:
Find the area between the cubic \(y=x^3-x^2\) and the line \(y=2x\).
The curves intersect when \[\begin{aligned} x^3-x^2&=2x \\ x^3-x^2-2x&=0 \\ x(x+1)(x-2)&=0 \\ x&=-1,0,2 \end{aligned}\] Between \(x=-1\) and \(x=0\), the cubic is above the line. Between \(x=0\) and \(x=2\), the line is above the cubic. So the area is
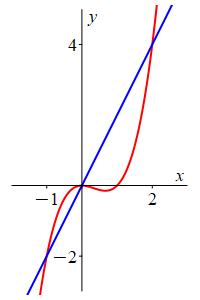
\[\begin{aligned} A&=\int_{-1}^0 (x^3-x^2-2x)\,dx +\int_0^2 (2x-x^3+x^2)\,dx \\ &=\left[\dfrac{x^4}{4}-\dfrac{x^3}{3}-x^2\right]_{-1}^0 +\left[x^2-\dfrac{x^4}{4}+\dfrac{x^3}{3}\right]_0^2 \\ &=(0)-\left(\dfrac{1}{4}-\dfrac{-1}{3}-1\right) +\left(4-4+\dfrac{8}{3}\right)-(0) \\ &=\dfrac{-3-4+12+32}{12}=\dfrac{37}{12} \end{aligned}\]
Find the area between the curve \(y=x^3-4x^2+4x=x(x-2)^2\) and the parabola \(y=x^2\).
To find the intersection points, equate the functions: \[x^3-4x^2+4x=x^2\]
\(\displaystyle A=\int_0^1 (x^3-4x^2+4x)-x^2\,dx+\int_1^4 x^2-(x^3-4x^2+4x)\,dx =\dfrac{71}{6}\)
To plot the cubic, we note that its \(x\)-intercepts are at \(0\) and \(2\), it is negative when \(x\) is negative and positive when \(x\) is positive. So there must be a local minimum at \(x=2\). To find the intersection points, we equate the functions: \[\begin{aligned} x^3-4x^2+4x&=x^2 \\ x^3-5x^2+4x&=0 \\ x(x-1)(x-4)&=0 \\ x=0,1,4& \end{aligned}\] So the area is
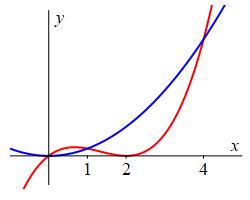
\[\begin{aligned} A&=\int_0^1 \text{upper}-\text{lower}\,dx +\int_1^4 \text{upper}-\text{lower}\,dx \\ &=\int_0^1 (x^3-4x^2+4x)-x^2\,dx +\int_1^4 x^2-(x^3-4x^2+4x)\,dx \\ &=\int_0^1 x^3-5x^2+4x\,dx +\int_1^4-x^3+5x^2-4x\,dx \\ &=\left[\dfrac{x^4}{4}-\dfrac{5x^3}{3}+2x^2\right]_0^1 +\left[-\dfrac{x^4}{4}+\dfrac{5x^3}{3}-2x^2\right]_1^4 =\dfrac{71}{6} \end{aligned}\]
You can practice computing Areas between Curves which Cross by using the following Maplets (requires Maple on the computer where this is executed):
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum