19. Properties of Graphs

b. Value & Limit Information

When \(\lim_{x\to-\infty}f(x)\) or \(\lim_{x\to\infty}f(x)\) is not a finite number, i.e. there is no horizontal asymptote, we may still want to understand the behavior of the function near \(-\infty\) and \(\infty\).

3. Slant Asymptotes (Optional)

A slant asymptote of a function \(f(x)\) is a line \(y=mx+b\) where \[ \lim_{x\to-\infty}f(x)-(mx+b)=0 \quad \text{or} \quad \lim_{x\to\infty}f(x)-(mx+b)=0 \]

A slant asymptote will look something like one of the following: (The asymptote could be at \(+\infty\) or \(-\infty\). The slope could be positive or negative and the approach could be from above or below.)

 

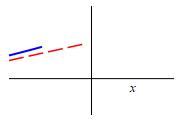
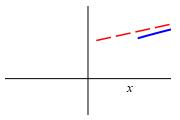
To find a slant asymptote at \(-\infty\), we compute the limits: \[ m_-=\lim_{x\to-\infty}\dfrac{f(x)}{x} \quad \text{and} \quad b_-=\lim_{x\to-\infty}f(x)-m_-x \] If these limits exist, the slant asymptote is \(y=m_-x+b_-\). Similarly, at \(+\infty\), if the limits: \[ m_+=\lim_{x\to\infty}\dfrac{f(x)}{x} \quad \text{and} \quad b_+=\lim_{x\to\infty}f(x)-m_+x \] exist, the slant asymptote is \(y=m_+x+b_+\).

Find the slant asymptotes of the function \(f(x)=2x-\dfrac{16}{x-2}\).
This is the same function as the example on two previous pages.

We compute the limits: \[\begin{aligned} m_-&=\lim_{x\to-\infty}\dfrac{f(x)}{x} =\lim_{x\to-\infty}2-\dfrac{16}{x(x-2)}=2 \\ b_-&=\lim_{x\to-\infty}f(x)-2x =\lim_{x\to-\infty}-\dfrac{16}{x-2}=0 \end{aligned}\] So the slant asymptote at \(-\infty\) is \(y=2x\). Similarly: \[\begin{aligned} m_+&=\lim_{x\to\infty}\dfrac{f(x)}{x} =\lim_{x\to\infty}2-\dfrac{16}{x(x-2)}=2 \\ b_+&=\lim_{x\to\infty}f(x)-2x =\lim_{x\to\infty}-\dfrac{16}{x-2}=0 \end{aligned}\] So the slant asymptote at \(\infty\) is also \(y=2x\). We add these facts to the number line: