19. Properties of Graphs

b. Value & Limit Information

2. Vertical Asymptotes

A vertical asymptote of a function \(f(x)\) is a vertical line \(x=a\) where \[ \lim_{x\to a^-}f(x)=\pm\infty \quad \text{or} \quad \lim_{x\to a^+}f(x)=\pm\infty \]

If \(f(x)\) is a fraction, the vertical asymptotes are the points where the denominator is zero. Once we find a vertical asymptotes, \(x=a\), we compute the limits: \[ \lim_{x\to a^-}f(x) \quad \text{and} \quad \lim_{x\to a^+}f(x) \] to determine which of the following plots represents the qualitative behavior of the graph of \(f(x)\).
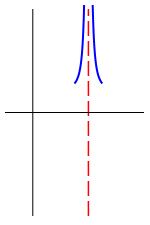
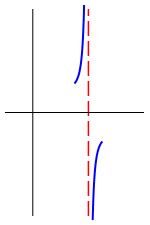
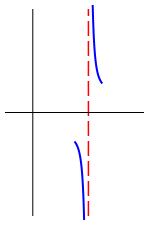
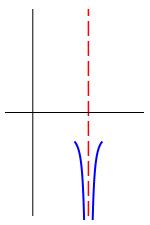
def_vasympt_upup def_vasympt_updn def_vasympt_dnup def_vasympt_dndn
Up-Up Up-Down Down-Up Down-Down

Find the vertical asymptotes of the function \(f(x)=2x-\dfrac{16}{x-2}\). For each asymptote \(x=a\), compute the limits \(\displaystyle \lim_{x\to a^-}f(x)\) and \(\displaystyle \lim_{x\to a^+}f(x)\) and determine if the qualitative behavior of the graph is up-up, up-down, down-up or down-down.
This is the same function as in the example on the previous page.

We first notice that the function is undefined at \(x=2\) which is the location of the vertical asymptote. Next, to compute the limits, we rewrite the function as: \[ f(x)=\dfrac{2x(x-2)-16}{x-2}=\dfrac{2(x+2)(x-4)}{x-2} \] In computing the limits, we will write \(b^+\) to mean a number slightly larger than \(b\) and \(b^-\) to mean a number slightly smaller than \(b\). First, the limit from the left is: \[\begin{aligned} \lim_{x\to 2^-}f(x)&=\lim_{x\to 2^-}\dfrac{2(x+2)(x-4)}{x-2} \\ &=``\dfrac{2(2^-+2)(2^--4)}{2^--2}"=``\dfrac{2(4^-)(-2^-)}{0^-}"=\infty \end{aligned}\] In the last step \(4^-\) is slightly less than \(4\) and so is positive and \(-2^-\) is slightly less than \(-2\) and so is negative. Together, we have positive times negative divided by negative which gives positive. 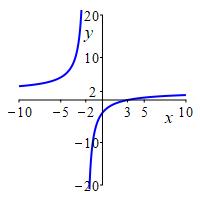Similarly, the limit from the right is: \[\begin{aligned} \lim_{x\to 2^+}f(x)&=\lim_{x\to 2^+}\dfrac{2(x+2)(x-4)}{x-2} \\ &=``\dfrac{2(2^++2)(2^+-4)}{2^+-2}"=``\dfrac{2(4^+)(-2^+)}{0^+}"=-\infty \end{aligned}\] So the qualitative behavior is up-down. We add these facts to the number line: eg_2x-16_(x-2)_number_line_vasympt

In the plot, we can now see the vertical asymptote at \(x=2\) which is approached upward on the left and downward on the right.

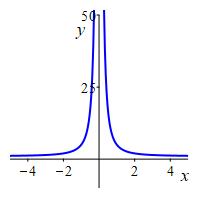
Find the vertical asymptotes of the function \(f(x)=1+\dfrac{4}{x^2}\). For each asymptote \(x=a\), compute the limits \(\displaystyle \lim_{x\to a^-}f(x)\) and \(\displaystyle \lim_{x\to a^+}f(x)\) and determine if the qualitative behavior of the graph is up-up, up-down, down-up or down-down.
This is the same function as in an exercise on the previous page.

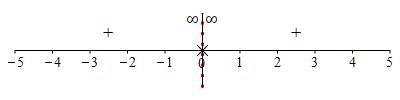
The vertical asymptote is at \(x=0\). The function approaches the asymptote upward on both sides: ex_1+4_x^2_number_line_vasympt

The vertical asymptote is at \(x=0\). So we compute the limits: \[\begin{aligned} \lim_{x\to 0^-}f(x)&=\lim_{x\to 0^-}1+\dfrac{4}{x^2} =``1+\dfrac{4}{(0^-)^2}"=\infty \\ \lim_{x\to 0^+}f(x)&=\lim_{x\to 0^+}1+\dfrac{4}{x^2} =``1+\dfrac{4}{(0^+)^2}"=\infty \end{aligned}\] So the function approaches the asymptote upward on both sides: ex_1+4_x^2_number_line_vasympt

In the plot, we can now see the vertical asymptote at \(x=0\) which is approached upward on both sides.

Find the vertical asymptotes of the function \(f(x)=\dfrac{2x^2-10x+12}{x^2-4}\). For each asymptote \(x=a\), compute the limits \(\displaystyle \lim_{x\to a^-}f(x)\) and \(\displaystyle \lim_{x\to a^+}f(x)\) and determine if the qualitative behavior of the graph is up-up, up-down, down-up or down-down.
This is the same function as in an exercise on the previous page.

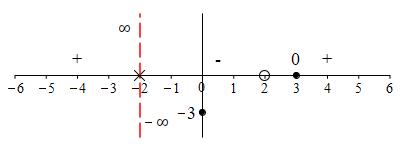
The vertical asymptote is at \(x=-2\). The function approaches the asymptote upward in the left and downward on the right: ex_2x^2-10x+12_x^2-4_number_line_vasympt

Since \(f(x)=\dfrac{2(x-3)}{x+2}\) except at \(x=2\), the vertical asymptote is at \(x=-2\). 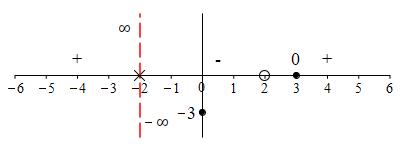We compute the limits: \[\begin{aligned} \lim_{x\to -2^-}f(x)&=\lim_{x\to -2^-}\dfrac{2(x-3)}{x+2} =``\dfrac{2(-5)}{0^-}"=\infty \\ \lim_{x\to -2^+}f(x)&=\lim_{x\to -2^+}\dfrac{2(x-3)}{x+2} =``\dfrac{2(-5)}{0^+}"=-\infty \end{aligned}\] So the function approaches the asymptote upward in the left and downward on the right: ex_2x^2-10x+12_x^2-4_number_line_vasympt

In the plot, we can now see the vertical asymptote at \(x=-2\) which is approached upward on the left and downward on the right.

19. Properties of Graphs

b. Value & Limit Information

2. Vertical Asymptotes

Heading