12. Differentials & Linear Approximation
c. Mean Value Theorem
1. Proof
Before we can prove the Mean Value Theorem, we need to prove Rolle's Theorem.
If \(g(x)\) is a function on the interval \([a,b]\) with a continuous derivative, \(g'(x)\), and \(g(a)=g(b)\) then there is a number \(c\) in \((a,b)\) such that \[ g'(c)=0. \]
Look at this plot showing \(4\) continuous functions satisfying \(g(a)=g(b)\):
one which has the constant value \(g(a)\) red \(g(x) =g(a)\) one which is always bigger than \(g(a)\) blue \(g(x) \geq g(a)\) one which is always smaller than \(g(a)\), cyan \(g(x) \leq g(a)\) and one which is sometimes bigger and sometimes smaller than \(g(a)\). orange \(g(x)\ \) sometimes \(\ \gt g(a)\) and \(g(x)\ \) sometimes \(\ \lt g(a)\)
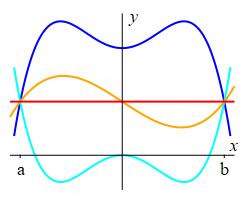
Since \(g(x)\) is continuous, by the Extreme Value Theorem it must have a maximum and a minimum somewhere in \([a,b]\). If \(g\) is constant, then every point is both a maximum and minimum. Since \(g(a)=g(b)\), if \(g\) is not constant, then it must go up or down somewhere (as in the plot) and have a maximum or minimum somewhere in \((a,b)\). Let \(c\) be a number in \((a,b)\) where \(g(c)\) is a maximum or minimum. Since \(g(x) \) is differentiable, the slope of the tangent line is \(0\) at \(x=c\), in other words, \[ g'(c)=0 \]
There may be more than one number \(c\) where \(g'(c)=0\). The theorem only guarantees that there is at least one.
If \(f(x)\) is a function on the interval \([a,b]\) with a continuous derivative, \(f'(x)\), then there is a number \(c\) in \((a,b)\) such that \[ f'(c)=\dfrac{f(b)-f(a)}{b-a} \] or equivalently, \[ f(b)=f(a)+f'(c)(b-a) \]
The equation of the line between the endpoints is \[ y=f(a)+\dfrac{f(b)-f(a)}{b-a}(x-a) \]
Why is this a line?
It is a line because \(y\) is a linear function of \(x\). In particular, it is the point-slope form of the line, \(y=f(a)+m(x-a)\), where the slope is \(m=\dfrac{f(b)-f(a)}{b-a}\).
Why does it go through the endpoints?
When \(x=a\), \[ y=f(a)+\dfrac{f(b)-f(a)}{b-a}(a-a)=f(a) \] When \(x=b\), \[ y=f(a)+\dfrac{f(b)-f(a)}{b-a}(b-a)=f(b) \]
We define a new function \(g(x)\) which is the difference between our original function \(f(x)\) and the straight line between the endpoints: \[ g(x)=f(x)-f(a)-\dfrac{f(b)-f(a)}{b-a}(x-a) \] We evaluate \(g(x)\) at the endpoints and also compute its derivative: \[\begin{aligned} g(a)&=f(a)-f(a)-\dfrac{f(b)-f(a)}{b-a}(a-a)=0 \\ g(b)&=f(b)-f(a)-\dfrac{f(b)-f(a)}{b-a}(b-a)=0 \\ g'(x)&=f'(x)-\dfrac{f(b)-f(a)}{b-a} \end{aligned}\] Since \(g(a)=g(b)\), we can apply Rolle's Theorem to \(g(x)\) to conclude there is a number \(c\) in \((a,b)\) such that \(g'(c)=0\). But this says: \[ f'(c)-\dfrac{f(b)-f(a)}{b-a}=0 \] which is the Mean Value Theorem.