6. Differentials & Linear Approximation
Exercises
-
Consider the function \(f(x)=x^2\).
-
Find the tangent line at \(x=3\).
The equation of the tangent line at \(x=a\) is: \[ y=f(a)+f'(a)(x-a) \]
\(y=9+6(x-3)=6x-9\)
The function is: \[ f(x)=x^2 \] The function value at \(x=3\) is: \[ f(3)=9 \] The derivative is: \[ f'(x)=2x \] At \(x=3\) the derivative is: \[ f'(3)=6 \]
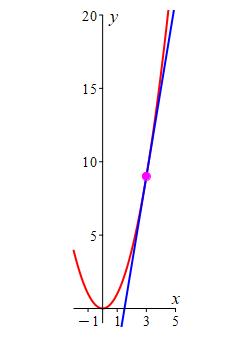
So the tangent line is: \[\begin{aligned} y&=f(3)+f'(3)(x-3) \\ &=9+6(x-3) =6x-9 \end{aligned}\] The plots of the function and the tangent line are shown.
sw
-
Find the change in \(x\) and the change in the function between \(a=3\) and \(x=3.2\).
The changes are \[\begin{aligned} \Delta x&=x-a \\ \Delta f&=f(x)-f(a) \end{aligned}\]
\(\begin{aligned} \Delta x&=.2 \\ \Delta f&=1.24 \end{aligned}\)
The change in \(x\) is: \[ \Delta x=x-a=3.2-3=0.2 \] The change in \(f\) is: \[\begin{aligned} \Delta f&=f(x)-f(a)=f(3.2)-f(3) \\ &=3.2^2-3^2=1.24 \end{aligned}\]
sw
-
Find the differential of \(x\) and the differential of the function between \(a=3\) and \(x=3.2\).
The differentials are \[\begin{aligned} dx&=x-a \\ df&=f_{\text{tan}}(x)-f(a)=f'(a)\,dx \end{aligned}\]
\(\begin{aligned} dx&=0.2 \\ df&=1.2 \end{aligned}\)
The differential of \(x\) is \[ dx=x-a=3.2-3=0.2 \] Since \(f'(3)=6\), the differential of \(f(x)\) is \[ df=f'(3)\, dx=6\cdot 0.2=1.2 \]
sw
We check by computing the differential by a different method.
We know \(f_{\text{tan}}(x)=9+6(x-3)\). So: \[ f_{\text{tan}}(3.2)=9+6(3.2-3)=10.2 \] and \[ df=f_{\text{tan}}(3.2)-f(3) =10.2-9=1.2 \] The second method is longer, because we are essentailly adding and subtracting \(9\).
-
-
Consider the function \(g(x)=2x^2+3x+5\).
-
Find the tangent line at \(x=2\).
The tangent line to a function at \(x=a\) is: \[ y=g(a)+g'(a)(x-a) \]
\(y=19+11(x-2)=11x-3\)
The function at \(x=2\) is: \[ g(2)=2\cdot 2^2+3\cdot 2+5=19 \] The derivative is: \[ g'(x)=4x+3 \] The derivative at \(x=2\) is: \[ g'(2)=4\cdot 2+3=11 \] The tangent line at \(x=2\) is: \[\begin{aligned} y&=g(2)+g'(2)(x-2) \\ &=19+11(x-2)=11x-3 \end{aligned}\]
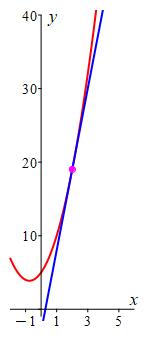
The plots of the function and the tangent line are shown.
sw
-
Find the change in \(x\) the function between \(a=2\) and \(x=2.1\).
The changes are \[\begin{aligned} \Delta x&=x-a \\ \Delta g&=g(x)-g(a) \end{aligned}\]
\(\begin{aligned} \Delta x&=0.1 \\ \Delta g&=1.12 \end{aligned}\)
The change in \(x\) is: \[ \Delta x=x-a=2.1-2=0.1 \] Since \(g(2.1)=2(2.1)^2+3(2.1)+5=20.12\), the change in \(g\) is: \[ \begin{aligned} \Delta g &=g(x)-g(a)=g(2.1)-g(2)\\ &=20.12-19=1.12 \end{aligned} \]
sw
-
Find the differential of \(x\) and the differential of the function between \(a=2\) and \(x=2.1\).
The differentials are \[\begin{aligned} dx&=x-a \\ dg&=g_{\text{tan}}(x)-g(a)=g'(a)\,dx \end{aligned}\]
\(dx=0.1\)
\(dg=1.1\)The differential of \(x\) is: \[ \, dx=x-a=2.1-2=0.1 \] Since \(g'(2)=11\), the differential of \(g(x)\) is: \[ dg=g'(2)dx=11\cdot 0.1=1.1 \] Alternatively, since \(g_{\text{tan}}(x)=19+11(x-2)\), we have \(g_{\text{tan}}(2.1)=19+11(.1)=20.1\) and so: \[ dg=g_{\text{tan}}(2.1)-g(2) =20.1-19=1.1 \] The second method is longer, because we are essentailly adding and subtracting \(19\).
sw
-
-
Consider the function \(p(x)=x^3-\dfrac{4}{x}\).
-
Find the tangent line at \(x=2\).
The tangent line to a function at \(x=a\) is: \[ y=p(a)+p'(a)(x-a) \]
\(y=6+13(x-2)=13x-20\)
The function at \(x=2\) is: \[ p(2)=2^3-\frac{4}{2}=6 \] The derivative is: \[ p'(x)=3x^2+\frac{4}{x^2} \] The derivative at \(x=2\) is: \[ p'(2)=3\cdot2^2+\frac{4}{2^2}=13 \] So the tangent line is: \[\begin{aligned} y&=p(2)+p'(2)(x-2) \\ &=6+13(x-2) =13x-20 \end{aligned}\]
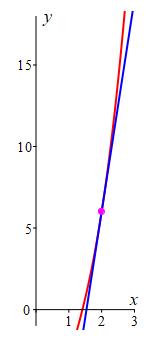
The plots of the function and the tangent line are shown.
sw
-
Find the change in \(x\) and the change in the function between \(a=2\) and \(x=2.3\).
The changes are \[\begin{aligned} \Delta x&=x-a \\ \Delta p&=p(x)-p(a) \end{aligned}\]
\(\begin{aligned} \Delta x&=0.3 \\ \Delta p&=4.43 \end{aligned}\)
The change in \(x\) is: \[ \Delta x=x-a=2.3-2=0.3 \] Since \[ p(2)=6 \quad \text{and} \quad p(2.3)=2.3^3-\dfrac{4}{2.3}\approx10.43 \] the change in \(p(x)\) is: \[\begin{aligned} \Delta p&=p(x)-p(a)=p(2.3)-p(2) \\ &\approx10.43-6=4.43 \end{aligned}\]
sw
-
Find the differential of \(x\) and the differential of the function between \(a=2\) and \(x=2.3\).
The differentials are \[\begin{aligned} dx&=x-a \\ dp&=p_{\text{tan}}(x)-p(a)=p'(a)\,dx \end{aligned}\]
\(\begin{aligned} dx&=0.3 \\ dp&=3.9 \end{aligned}\)
The differential of \(x\) is: \[ dx=x-a=2.3-2=0.3 \] Since \(p'(2)=13\) the differential of \(p(x)\) is: \[ dp=p'(2)\,dx=13\cdot 0.3=3.9 \] Alternatively, since \(p_{\text{tan}}(x)=6+13(x-2)\), we have \(p_{\text{tan}}(2.3)=6+13(.3)=9.9\) and so: \[ dp=p_{\text{tan}}(2.3)-p(2) =9.9-6=3.9 \]
sw
-
-
A spherical ballon of radius \(r=6\,\text{cm}\) slowly leaks. If the radius of the ballon decreases \(0.4\,\text{cm}\), find the change and differential of the volume of the balloon. (The volume of a sphere is \(V=\dfrac{4}{3}\pi r^3\).)
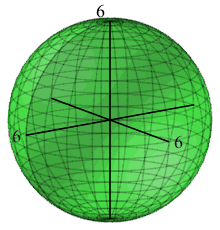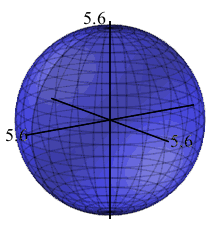
\(\Delta V=-169.16\)
\(dV=-180.96\)The old volume was: \[ V_i=\dfrac{4}{3}\pi 6^3=288\pi \] The new volume is: \[ V_f=\dfrac{4}{3}\pi 5.6^3=234.154\overline{6}\pi \] So the change in volume is: \[\begin{aligned} \Delta V&=234.154\overline{6}\pi-288\pi\\ &=-53.845\overline{3}\pi=-169.16 \end{aligned}\] To find the differential we need the derivative:: \[\begin{aligned} V'(r)&=4\pi r^2\\ V'(6)&=4\pi (6)^2=144\pi \end{aligned}\] Then, the differential is: \[\begin{aligned} dV&=V'(6)\,dr =144\pi(-0.4) \\ &=-57.6\pi=-180.96 \end{aligned}\] So the differential is a reasonable approximation to the change. The plot shows the old and new volumes
sw
-
Use a linear approximation to estimate \(\sqrt[\scriptsize3]{27.4}\).
Which value \(x\) near \(27.4\) gives a simple value for \(\sqrt[\scriptsize3]{x}\)? Approximate near that value.
\(\sqrt[\scriptsize3]{27.4}\approx3.0\overline{148}\).
We take \(f(x)=\sqrt[\scriptsize3]{x}=x^{1/3}\), since we know \(f(27)=3\). We then construct the tangent function. We have: \[\begin{aligned} f'(x)&=\dfrac{1}{3}x^{-2/3}=\dfrac{1}{3\sqrt[\scriptsize3]{x}^2} \\ f'(27)&=\dfrac{1}{3\sqrt[\scriptsize3]{27}^2}=\dfrac{1}{27} \end{aligned}\] So the tangent function is: \[\begin{aligned} f_{\text{tan}}(x)&=f(27)+f'(27)(x-27) \\ &=3+\dfrac{1}{27}(x-27) =\dfrac{1}{27}x+2 \end{aligned}\] Finally, let \(x=27.4\). Then: \[\begin{aligned} \sqrt[\scriptsize3]{27.4}&=f(27.4)\approx f_{\text{tan}}(27.4) \\ &=3+\dfrac{1}{27}(27.4-27) \\ &=3+\dfrac{0.4}{27}=3.0\overline{148} \end{aligned}\]
sw
The actual value of \(\sqrt[\scriptsize3]{27.4}\) is approximately \(3.01474\). Our approximation is \(3.0\overline{148}\). Since these are so close our approximation is an accurate one.
-
Use a linear approximation to estimate \(\dfrac{1}{\sqrt[\scriptsize4]{16.3}}\).
Which value \(x\) near \(16.3\) gives a simple value for \(\dfrac{1}{\sqrt[\scriptsize4]{x}}\)? Approximate near that value.
\(\dfrac{1}{\sqrt[\scriptsize4]{16.3}}\approx.49765625\).
We take \(f(x)=\dfrac{1}{\sqrt[\scriptsize4]{x}}=x^{-1/4}\), since we know \(f(16)=\dfrac{1}{2}\). We then construct the tangent function. We have: \[\begin{aligned} f'(x)&=-\,\dfrac{1}{4}x^{-5/4}=-\dfrac{1}{4\sqrt[\scriptsize4]{x}^5} \\ f'(16)&=-\,\dfrac{1}{4\sqrt[\scriptsize4]{16}^5}=-\,\dfrac{1}{128} \end{aligned}\] So the tangent function is: \[\begin{aligned} f_{\text{tan}}(x)&=f(16)+f'(16)(x-16) \\ &=\dfrac{1}{2}-\dfrac{1}{128}(x-16) =-\dfrac{1}{128}x+\dfrac{5}{8} \end{aligned}\] Finally, let \(x=16.3\). Then: \[\begin{aligned} \dfrac{1}{\sqrt[\scriptsize4]{16.3}}&=f(16.3)\approx f_{\text{tan}}(16.3) \\ &=\dfrac{1}{2}-\dfrac{1}{128}(16.3-16) \\ &=\dfrac{1}{2}-\dfrac{0.3}{128}=.49765625 \end{aligned}\]
sw
The actual value of \(\dfrac{1}{\sqrt[\scriptsize4]{16.3}}\) is approximately \(0.497683\). Our approximation was \(0.49765625\). Since these are so close our approximation is an accurate one.
-
A conical cup is filled with water to a height \(h=9\,\text{cm}\) and radius \(r=2\,\text{cm}\), but it is leaking. If \(0.5\,\text{cm}^3\) leaks out, estimate the change in the height of the water.
(The volume of a cone is \(V=\dfrac{1}{3}\pi r^2h\).)
Express the volume in terms of \(h\) only.
\(\Delta h\approx0.03979\,\text{cm}\).
Since \(\dfrac{h}{r}=\dfrac{9}{2}\), we can write \(r\) as \(r=\dfrac{2}{9}h\). Plugging that into the volume of the cone we get: \[ V=\dfrac{1}{3}\pi \left(\dfrac{2}{9}h\right)^2h =\dfrac{4}{243}\pi h^3 \] To get the change in the height, we approximate the change in the volume using differentials: \[ \Delta V\approx dV=\dfrac{dV}{dh}\,dh\approx\dfrac{4}{81}\pi h^2\Delta h \] We now solve for \(\Delta h\): \[ \Delta h\approx\dfrac{81}{4\pi h^2}\Delta V =\dfrac{81}{4\pi (9)^2}0.5=\dfrac{1}{8\pi} \approx0.03979 \]
sw
The initial volume is \[ V_i=\dfrac{4}{243}\pi (9)^3=12\pi \] The final volume is \[ V_f=12\pi-.5 \] The initial height is \[ h_i=9 \] The final height is \[ h_f=\left(\dfrac{243(12\pi-.5)}{4\pi}\right)^{1/3} =8.9601 \] The actual change in height is: \[ \Delta h=9-8.9601=.0399 \] Our estimate is: \[ \Delta h\approx0.03979 \] Since these are so close our estimate is an accurate one.
-
A little girl is pouring sand from a bucket forming a cone whose radius is always twice it height. Currently, the radius is \(r=4\,\text{cm}\). If she pours \(5\,\text{cm}^3\) more sand on the pile, how much does the radius change?
(The volume of a cone is \(V=\dfrac{1}{3}\pi r^2h\).)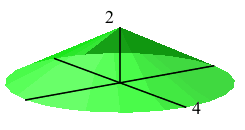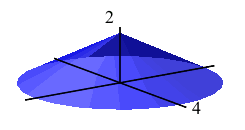
Express the volume in terms of \(r\) only.
\(\Delta r=\dfrac{5}{8\pi}\approx0.19894\)
Since the radius is always twice the height, we have \(r=2h\) or \(h=\dfrac{r}{2}\). We can write the volume of the sand as: \[ V=\dfrac{1}{3}\pi r^2h =\dfrac{1}{3}\pi r^2\dfrac{r}{2} =\dfrac{1}{6}\pi r^3 \] So \(\dfrac{dV}{dr}=\dfrac{1}{2}\pi r^2\). To get the change in the radius, we compute the change in the volume using differentials: \[ \Delta V\approx dV=\dfrac{dV}{dr}\,dr\approx \dfrac{1}{2}\pi r^2\Delta r \] We now solve for \(\Delta r\): \[ \Delta r\approx\dfrac{2}{\pi r^2}\Delta V =\dfrac{2}{\pi (4)^2}5=\dfrac{5}{8\pi} \approx0.19894 \]
sw
The initial volume is \[ V_i=\dfrac{1}{6}\pi (4)^3=33.51 \] The final volume is \[ V_f=33.51+5=38.51 \] The initial radius is \[ r_i=4 \] The final radius is \[ r_f=\sqrt[\scriptsize 3]{\dfrac{6V_f}{\pi}} =\sqrt[\scriptsize 3]{\dfrac{6(38.51)}{\pi}} \approx 4.1898 \] So the actual change in radius is: \[ \Delta r=4.1898-4=0.1898 \] Our estimate: \[ \Delta r\approx0.19894 \] is reasonable.
-
Consider the function \(f(x)=x^3\) on the interval \([-3,3]\). Find the number(s) \(c\in (-3,3)\) which are guaranteed to exist by the MVT.
Find where the derivative is equal to the slope between the endpoints.
\(c=\sqrt{3},-\sqrt{3}\)
The values at the endpoints are: \[ f(-3)=-27 \qquad f(3)=27 \] The slope between the endpoints is: \[ m=\dfrac{f(3)-f(-3)}{3-(-3)}=\dfrac{27-(-27)}{6}=9 \] The derivative is: \[ f'(x)=3x^2 \] So the Mean Value Theorem guarantees there is a number \(c\in(-3,3)\) where: \[ f'(c)=3c^2=9 \] So \(c=\sqrt{3},-\sqrt{3}\).
sw
We check by evaluating the derivative \(f'(x)=3x^2\) at \(c=\sqrt{3}\) and \(c=-\sqrt{3}\): \[\begin{aligned} f'(\sqrt{3})&=3(\sqrt{3})^2=9 \\ f'(-\sqrt{3})&=3(-\sqrt{3})^2=9 \end{aligned}\] Here is a plot of the function, the line between the endpoints and the tangent lines at \(c=\sqrt{3}\) and \(c=-\sqrt{3}\). Notice the tangent lines are parallel to the line between the endpoints.
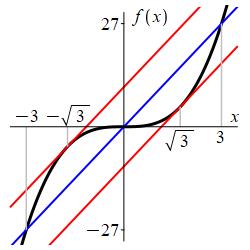
-
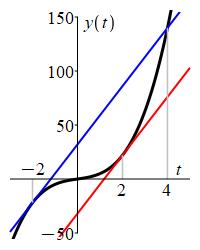
Consider the function \(y(t)=2t^3+3t\) on the interval \([-2,4]\). Find the number(s) \(c\in (-2,4)\) which are guaranteed to exist by the MVT.
Find where the derivative is equal to the slope between the endpoints.
\(c=2,-2\)
The values at the endpoints are: \[ y(-2)=-16-6=-22 \qquad y(4)=128+12=140 \] The slope between the endpoints is: \[ m=\dfrac{y(4)-y(-2)}{4-(-2)}=\dfrac{140-(-22)}{6}=27 \] The derivative is: \[ y'(t)=6t^2+3 \] So the Mean Value Theorem guarantees there is a number \(c\in(-2,4)\) where: \[ y'(c)=6c^2+3=27 \] or \(6c^2=24\) or \(c=2,-2\).
Technically, \(c=-2\) is not a solution guaranteed by the MVT, since it is an endpoint of the interval.
sw
We check by evaluating the derivative \(y'(t)=6t^2+3\) at \(c=2\) and \(c=-2\): \[ y'(2)=6(2)^2+3=27 \qquad y'(-2)=6(-2)^2+3=27 \] Here is a plot of the function, the line between the endpoints and the tangent lines at \(c=2\) and \(c=-2\). Notice the tangent lines are parallel to the line between the endpoints.
-
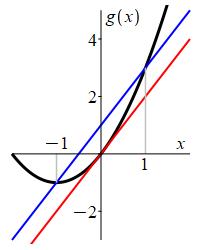
Consider the function \(g(x)=x^2+2x\) on the interval \([-1,1]\). Find the number(s) \(c\in (-1,1)\) which are guaranteed to exist by the MVT.
Find where the derivative is equal to the slope between the endpoints.
\(c=0\)
The values at the endpoints are: \[ g(-1)=-1 \qquad g(1)=3 \] The slope between the endpoints is: \[ m=\dfrac{g(1)-g(-1)}{1-(-1))}=\dfrac{3-(-1)}{2}=2 \] The derivative is: \[ g'(x)=2x+2 \] So the Mean Value Theorem guarantees there is a number \(c\in (-1,1)\) where: \[ g'(c)=2c+2=2 \] So \(c=0\)
sw
We check by evaluating the derivative \(g'(x)=2x+2\) at \(c=0\): \[ g'(0)=2(0)+2=2 \] Here is a plot of the function, the line between the endpoints and the tangent line at \(c=0\). Notice the tangent line is parallel to the line between the endpoints.
-
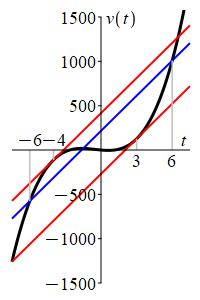
Consider the function \(v(t)=4t^3+6t^2-12t\) on the interval \((-6,6)\). Find the number(s) which are guaranteed to exist by the MVT.
Find where the derivative is equal to the slope between the endpoints.
\(c=-4,3\)
The values at the endpoints are: \[\begin{aligned} f(-6)&=-4(216)+6(36)+12(6)=-864+216+72=-576 \\ f(6)&=4(216)+6(36)-12(6)=864+216-72=1008 \end{aligned}\] The slope between the endpoints is: \[ m=\dfrac{v(6)-v(-6)}{6-(-6)}=\dfrac{1008-(-576)}{12}=132 \] The derivative is: \[ v'(t)=12t^2+12t-12 \] So the Mean Value Theorem guarantees there is a number \(c\in (-6,6)\) where: \[ v'(c)=12c^2+12c-12=132 \] If we factor we get: \[ 0=12c^2+12c-144=12(c+4)(c-3) \] So \(c=-4,3\).
sw
We check by evaluating the derivative \(v'(t)=12c^2+12c-12\) at \(c=-4\) and \(c=3\): \[\begin{aligned} v'(-4)&=12(16)+12(-4)-12=132 \\ v'(3)&=12(9)+12(3)-12=132 \end{aligned}\] Here is a plot of the function, the line between the endpoints and the tangent lines at \(c=-4\) and \(c=3\). Notice the tangent lines are parallel to the line between the endpoints.
-
Aggie drives from College Station to Houston, a 96 mile drive, with a maximum speed limit of 70 mi per hour. She texts her mom she is leaving at 9:47 AM and arrives home at 10:58. A policeman takes her to court over these numbers. How can the policeman prove to the mathematician on the jury that she was speeding?
If \(x(t)\) is the car's position as a function of time, the Mean Value Theorem says there is a number \(c\) between \(a\) and \(b\) such that: \[ x'(c)=\dfrac{x(b)-x(a)}{b-a} \]
Let \(x(t)\) be the car's position as a function of time. It's derivative is the car's velocity, \(v(t)=x'(t)\). The Mean Value Theorem says there is a number \(c\) between \(t=9:47\approx9.783\,\text{hr}\) and \(t=10:58\approx10.983\,\text{hr}\) where \[ v(c)=x'(c)=\dfrac{96}{10.983-9.783}=80.0 \] So somewhere between College Station and Houston, she was driving at \(80\,\dfrac{\text{mi}}{\text{hr}}\) which was certainly speeding.
The Power Rule says \(\dfrac{d}{dx}x^n=nx^{n-1}\). So far we have only proved it when \(n\) is a positive integer. However, it actually works for any number \(n\). We will prove this in the chapter on Inverse Functions. In the next two problems, feel free to use the Power Rule with \(n=\dfrac{1}{3}\) and \(n=-\,\dfrac{1}{4}\)
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum