12. Differentials & Linear Approximation

c. Mean Value Theorem

The linear approximation formula can be made exact if we replace the slope at the tangent point by the slope at another point in the interval. However, this formula is purely theoretical since we have no way to know which point in the interval to use.

If \(f(x)\) is a function on the interval \([a,b]\) with a continuous derivative, \(f'(x) \), then there is a number \(c\) in \((a,b)\) such that: \[ f'(c)=\dfrac{f(b)-f(a)}{b-a} \] or equivalently, \[ f(b)=f(a)+f'(c)(b-a) \] \(\Leftarrow\Leftarrow\) The proof is actually understandable.

The first version says there is a point \(x=c\) where the slope of the function \(f'(c)\) is equal to the slope of the straight line between the endpoints.

The plot shows the function (in black), the line between the endpoints (in blue) and an animated line (in red) which is parallel to the line between the endpoints. Notice that for this curve, there are two places where the animated line becomes tangent to the curve (and turns cyan). The theorem says there is always such a point.

The second version is easier to understand if we replace \(b\) by \(x\). Then the second version says there is a number \(c\) in \((a,x)\) where \[ f(x)=f(a) +f'(c)(x-a) \] This looks like the linear approximation: \[ f(x)\approx f(a)+f'(a)(x-a) \] but the equation becomes exact when the derivative \(f'(a)\) is replaced by the \(f'(c)\). Unfortunately, there is no way to know which point to use since the theorem only says such a point exists, but not how to find it.

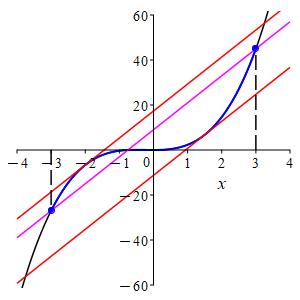
Consider the function \(f(x)=\dfrac{4}{3}x^3+x^2\) on the interval \([-3,3]\). Find the number(s) \(c\in(-3,3)\) which are guaranteed to exist by the Mean Value Theorem.

The values at the endpoints are: \[ f(-3)=-36+9=-27 \qquad f(3)=36+9=45 \] The slope between the endpoints is: \[ m=\dfrac{f(3)-f(-3)}{3--3}=\dfrac{45--27}{6}=12 \] The derivative is \[ f'(x)=4x^2+2x \] So the Mean Value Theorem guarantees there is a number \(c\in(-3,3)\) where \[ f'(c)=4c^2+2c=12 \] We rewrite the quadratic equation, factor it and solve: \[\begin{aligned} 4c^2+2c-12&=0 \qquad 2c^2+c-6=(c+2)(2c-3)=0 \\ c&=-2\quad\text{or}\quad\dfrac{3}{2} \end{aligned}\] The solutions could also be found using the quadratic formula: \[ c=\dfrac{-1\pm\sqrt{1-4(2)(-6)}}{4} =-2,\ \dfrac{3}{2} \]

We check by evaluating the slopes at the two values of \(c\): \[\begin{aligned} f'(-2)&=4(-2)^2+2(-2)=12 \\ f'\left(\dfrac{3}{2}\right) &=4\left(\dfrac{3}{2}\right)^2+2\left(\dfrac{3}{2}\right)=12 \end{aligned}\] The plot shows the function (in blue), the line between the endpoints (in magenta) and the tangent lines at \(c=-2\) and \(c=\dfrac{3}{2}\) (in red). Notice the tangent lines are parallel to the the line between the endpoints.

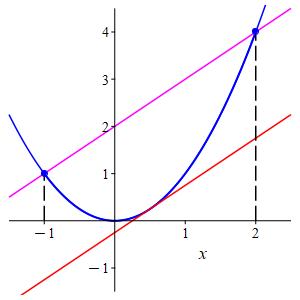
Consider the function \(f(x)=x^2\) on the interval \([-1,2]\). Find the number(s) \(c\in(-1,2)\) which are guaranteed to exist by the Mean Value Theorem.

Find where the derivative is equal to the slope between the endpoints.

\(\displaystyle c=\dfrac{1}{2}\)

The values at the endpoints are: \[ f(-1)=1 \qquad f(2)=4 \] The slope between the endpoints is: \[ m=\dfrac{f(2)-f(-1)}{2--1}=\dfrac{4-1}{3}=1 \] The derivative is \[ f'(x)=2x \] So the Mean Value Theorem guarantee there is a number \(c\in(-1,2)\) where \[ f'(c)=2c=1 \] So \(c=\dfrac{1}{2}\).

We check by evaluating the derivative \(f'(x)=2x\) at \(c=\dfrac{1}{2}\): \[ f'\left(\dfrac{1}{2}\right)=2\dfrac{1}{2}=1 \] The plot shows the function (in blue), the line between the endpoints (in magenta) and the tangent line at \(c=\dfrac{1}{2}\) (in red). Notice the tangent line is parallel to the the line between the endpoints.

12. Differentials & Linear Approximation

c. Mean Value Theorem

Heading