27. Gauss' Theorem

Let \(V\) be a nice solid region in \(\mathbb{R}^3\) with a nice properly oriented boundary, \(\partial V\), and let \(\vec F\) be a nice vector field on \(V\). Then \[ \iiint_V \vec\nabla\cdot\vec F\,dV =\iint_{\partial V} \vec F\cdot d\vec S \] The outer boundary must be oriented outward while any inner boundaries must be oriented inward. This means that all pieces of the boundary are oriented away from the solid.

d. Applications

Problems involving Gauss' Theorem have the potential to be confusing. When a problem asks you to compute the surface integral \(\displaystyle \iint_{\partial V} \vec F\cdot d\vec S\) using Gauss' Theorem, you probably need to compute the volume integral \(\displaystyle \iiint_V \vec\nabla\cdot\vec F\,dV\). Conversely, when a problem asks you to compute the volume integral \(\displaystyle \iiint_V \vec\nabla\cdot\vec F\,dV\) using Gauss' Theorem, you probably need to compute the surface integral \(\displaystyle \iint_{\partial V} \vec F\cdot d\vec S.\) The good news is that Gauss' Theorem frequently turns complicated integrals into relatively simple ones. Almost always you will be given the integral in its complex form, and it can be simplified by using Gauss' Theorem. In the real world, you won't know which is going to be easier.

1. Converting Surface Integrals to Volume Integrals

Most often, Gauss's Theorem is used to convert a surface integral over a closed surface into a region integral over the solid enclosed by the surface. These problems are discussed here. (Applications which go in the other direction are discussed on the next page.)

Compute the surface integral \(\displaystyle \iint_{\partial C} \vec F\cdot d\vec S\) where \(\vec F=\langle xy^2,yx^2,z(x^2+y^2)\rangle\) over the complete surface of the cylinder along the \(z\)-axis with radius \(r=3\) from \(z=0\) to \(z=5\) with outward normals.

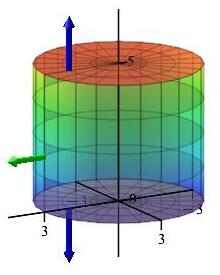
eg_appS2V_cyl

We are asked to compute the integral over the complete surface which would be the two disks at the ends plus the cylindrical sides. However, we can use Gauss' Theorem to simplify this problem to a volume integral \(\displaystyle \iiint_C \vec\nabla\cdot\vec F\,dV\). The integral is computed in cylindrical coordinates. We first compute the divergence in rectangular coordinates and then write it in cylindrical coordinates: \[ \vec\nabla\cdot\vec F=y^2+x^2+x^2+y^2=2(x^2+y^2)=2r^2 \] The volume differential is \(dV=r\,dr\,d\theta\,dz\) and the limits are \( 0 \le r \le 3\) and \(0 \le z \le 5\) and \(0 \le \theta \le 2\pi\), so the iterated integral is \[\begin{aligned} \iint_{\partial C} &\vec F\cdot d\vec S =\iiint_C \vec\nabla\cdot\vec F\,dV =\int_0^{2\pi}\int_0^5\int_0^3 (2r^2)r\,dr\,dz\,d\theta \\ &=\int_0^{2\pi} d\theta \int_0^5 dz \int_0^3 (2r^3)\,dr =(2\pi)(5)\left[\dfrac{r^4 }{2}\right]_0^3 =405\pi \end{aligned}\] Thus, instead of doing three separate surface integrals, Gauss' theorem allowed us to compute one volume integral.

Compute the surface integral \(\displaystyle \iint_{\partial P} \vec F\cdot d\vec S\) where \(\vec F=\langle xz,yz,z^2\rangle\) over the complete surface of the solid paraboloid \(3x^2+3y^2 \le z \le 12\) with outward normals.

ex_appS2V_parab

Always compute a divergence or curl in rectangular coordinates! It can be done in curvilinear coordinates, but it is much more complicated. When you are ready to do the integral, then you convert the divergence or curl into the coordinates needed for the integral.

\(\displaystyle \iint_{\partial P} \vec F\cdot d\vec S=768\pi\)

We use Gauss' Theorem to convert this problem to the volume integral \(\displaystyle \iiint_P \vec\nabla\cdot\vec F\,dV\). The integral is computed in cylindrical coordinates. We first compute the divergence in rectangular coordinates and then write it in cylindrical coordinates: \[ \vec\nabla\cdot\vec F=z+z+2z=4z \] The volume differential is \(dV=r\,dr\,d\theta\,dz\) and the \(z\) and \(\theta\) limits are \(3r^2 \le z \le 12\) and \(0 \le \theta \le 2\pi\). To find the upper limit for \(r\), we equate \(3r^2=12\) or \(r=2\). So the iterated integral is \[\begin{aligned} \iint_{\partial P} &\vec F\cdot d\vec S =\iiint_P \vec\nabla\cdot\vec F\,dV =\int_0^{2\pi}\int_0^2\int_{3r^2}^{12} (4z)r\,dz\,dr\,d\theta \\ &=2\pi\int_0^2 \left[\rule{0pt}{10pt}2z^2r\right]_{z=3r^2}^{12}\,dr =2\pi\int_0^2 (288r-18r^5)\,dr \\ &=2\pi\left[\rule{0pt}{10pt}144r^2-3r^6\right]_0^2 =8\pi(144-48) =768\pi \end{aligned}\] Thus, instead of doing two separate surface integrals, Gauss' theorem allowed us to compute one volume integral.

We check the problem by doing the surface integral directly. (This is significantly harder.) There are two pieces: the paraboloid oriented downward and the disk oriented upward.

Paraboloid:  We parameterize the paraboloid as: \[ \vec R(r,\theta)=(r\cos\theta,r\sin\theta,3r^2) \quad \text{for} \quad 0 \le r \le 2 \quad \text{and} \quad 0 \le \theta \le 2\pi \] We compute the normal vector \[\begin{aligned} \vec N &=\vec e_r\times\vec e_\theta= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos\theta & \sin\theta & 6r \\ -r\sin\theta & r\cos\theta & 0 \end{vmatrix} \\ &=\hat{\imath}(-6r^2\cos\theta) -\hat{\jmath}(6r^2\sin\theta) +\hat{k}(r\cos^2\theta+r\sin^2\theta) \\ &=\langle -6r^2\cos\theta,-6r^2\sin\theta,r\rangle \end{aligned}\] This is up and in. The normal vector needs to point down and out. So we reverse it: \[ \vec N=\langle 6r^2\cos\theta,6r^2\sin\theta,-r\rangle \] On the paraboloid the vector field, \(\vec F=\langle xz,yz,z^2\rangle\), is \[ \vec F =\langle 3r^3\cos\theta,3r^3\sin\theta,9r^4\rangle \] So the dot product with the normal is \[\begin{aligned} \vec F\cdot\vec N =18r^5\cos^2\theta+18r^5\sin^2\theta-9r^5 =9r^5 \end{aligned}\] We are ready to do the integral: \[\begin{aligned} \iint\limits_\text{paraboloid} \vec F\cdot d\vec S &=\int_0^{2\pi}\int_0^2 9r^5\,dr\,d\theta \\ &=2\pi\left[\dfrac{3r^6}{2}\right]_0^2=3\cdot2^6\pi =192\pi \end{aligned}\] Disk:  We parameterize the disk as: \[ \vec R(r,\theta)=(r\cos\theta,r\sin\theta,12) \quad \text{for} \quad 0 \le r \le 2 \quad \text{and} \quad 0 \le \theta \le 2\pi \] We compute the normal vector: \[ \vec N=\vec e_r\times\vec e_\theta= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos\theta & \sin\theta & 0 \\ -r\sin\theta & r\cos\theta & 0 \end{vmatrix} =\langle 0,0,r\rangle \] which correctly points upward. On the disk the vector field \(\vec F=\langle xz,yz,z^2\rangle\) is \[ \vec F =\langle 12r\cos\theta,12r\sin\theta,144\rangle \] So the dot product with the normal is just \[ \vec F\cdot\vec N=144r \] We are ready to do the integral: \[ \displaystyle \iint\limits_\text{disk} \vec F\cdot d\vec S =\int_0^{2\pi}\int_0^2 144r\,dr\,d\theta =2\pi\left[\rule{0pt}{10pt}72r^2\right]_0^2 =576\pi \] Total:  We add the integrals from the two pieces of the boundary: \[\begin{aligned} \iint\limits_{\partial S} \vec F\cdot d\vec s &=\iint\limits_\text{paraboloid} \vec F\cdot d\vec s +\iint\limits_\text{disk} \vec F\cdot d\vec s \\ &=192\pi+576\pi=768\pi \end{aligned}\] which agrees with the volume integral.

© MYMathApps

Supported in part by NSF Grant #1123255