27. Gauss' Theorem

Let \(V\) be a nice solid region in \(\mathbb{R}^3\) with a nice properly oriented boundary, \(\partial V\), and let \(\vec F\) be a nice vector field on \(V\). Then \[ \iiint_V \vec\nabla\cdot\vec F\,dV =\iint_{\partial V} \vec F\cdot d\vec S \] The outer boundary must be oriented outward while any inner boundaries must be oriented inward. This means that all pieces of the boundary are oriented away from the solid.

c. Proof

We will only prove Gauss' Theorem for solids without holes. For a solid with holes, we slice the solid into pieces without holes and add the results for all the pieces.

Overview

We will write the vector function \(\vec F\) as \[ \vec F=\langle P(x,y,z),Q(x,y,z),T(x,y,z)\rangle . \] and expand Gauss' Theorem as \[ \iiint_V (\partial_xP+\partial_yQ+\partial_zT)\,dV =\iint_{\partial V} P\,dy\,dz+Q\,dz\,dx+T\,dx\,dy \]

To write the right side in this form, we need to express the \(d\vec S\) vector in terms of the normal vector: \[\begin{aligned} d\vec S &=\vec N\,du\,dv =\left(\dfrac{\partial(y,z)}{\partial(u,v)}, \dfrac{\partial(z,x)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right)\,du\,dv \\ &=(dy\,dz,dz\,dx,dx\,dy)&&(*) \end{aligned}\] Then the right side is \(\vec F\cdot d\vec S\).

We will prove the theorem for the case that \(\vec F=\langle P,0,0\rangle\), and that only for the case of a rectangular solid box. Totally analogous proofs work for the other two cases \(\vec F=\langle 0,Q,0\rangle\) and \(\vec F=\langle 0,0,T\rangle\). They are assigned as exercises. The general result is then just the sum of the three special cases.

Proof of the \(P\) Piece

We prove \[ \iiint_V \partial_x P\,dV =\iint_{\partial V} P\,dy\,dz \] for the simple case of a rectangular box with bounds: \[ a \le x \le b \quad\text{and}\quad c \le y \le d \quad\text{and}\quad e \le z \le f \] To carry out the proof, we evaluate the left and right hand sides to see they are equal.

LHS RHS

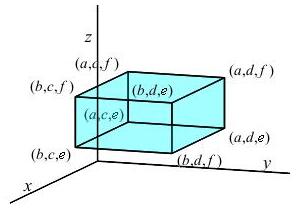
LHS:

To compute the integral on the left, we apply the Fundamental Theorem of Calculus to the \(x\)-integral while \(y\) and \(z\) are held constant: \[\begin{aligned} \iiint_V \partial_xP\,dV &=\int_e^f\int_c^d\int_a^b \partial_xP(x,y,z)\,dx\,dy\,dz \\ &=\int_e^f\int_c^d P(b,y,z)-P(a,y,z)\,dy\,dz \end{aligned}\] We now want to see that this is the same as the integral on the right.

RHS:

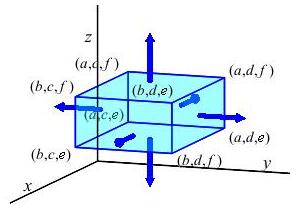
We know that \(\partial V\) is the surface of the box, which has \(6\) faces. To evaluate the right side we need to parameterize all six faces and find their normal vectors. In each case, we take \(\vec N=\vec e_u\times\vec e_v\) and choose \(u\) and \(v\) so that \(\vec N\) has the correct orientation. Also notice from equation (*) that \(dy\,dz\) is the first component of \(\vec N\) times \(\,du\,dv\).

\(\begin{aligned} &\rule{0pt}{10pt} \\ &\vec R_1(u,v)=(a,v,u) \\ &e \le u \le f \quad c \le v \le d \end{aligned} \quad \vec N_1= \begin{vmatrix} i & j & k \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{vmatrix} =(-1,0,0) \quad\, dy\,dz=-du\,dv \)
\(\begin{aligned} &\rule{0pt}{10pt} \\ &\vec R_2(u,v)=(b,u,v) \\ &c \le u \le d \quad e \le v \le f \end{aligned} \quad \vec N_2= \begin{vmatrix} i & j & k \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} =(1,0,0) \qquad dy\,dz=du\,dv\)
\(\begin{aligned} &\rule{0pt}{10pt} \\ &\vec R_3(u,v)=(u,c,v) \\ &a \le u \le b \quad e \le v \le f \end{aligned} \quad \vec N_3= \begin{vmatrix} i & j & k \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{vmatrix} =(0,-1,0) \quad\, dy\,dz=0\)
\(\begin{aligned} &\rule{0pt}{10pt} \\ &\vec R_4(u,v)=(v,d,u) \\ &e \le u \le f \quad a \le v \le b \end{aligned} \quad \vec N_4= \begin{vmatrix} i & j & k \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{vmatrix} =(0,1,0) \qquad dy\,dz=0\)
\(\begin{aligned} &\rule{0pt}{10pt} \\ &\vec R_5(u,v)=(v,u,e) \\ &c \le u \le d \quad a\le v \le b \end{aligned} \quad \vec N_5= \begin{vmatrix} i & j & k \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{vmatrix} =(0,0,-1) \quad\, dy\,dz=0\)
\(\begin{aligned} &\rule{0pt}{10pt} \\ &\vec R_6(u,v)=(u,v,f) \\ &a \le u \le b \quad c \le v \le d \end{aligned} \quad \vec N_6= \begin{vmatrix} i & j & k \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} =(0,0,1) \qquad dy\,dz=0\)

Notice that we have chosen the order of \(u\) and \(v\) in each parametrization so that the normal \(\vec N\) points out of the surface, i.e. toward

negative \(x\) when \(x=a\) and positive \(x\) when \(x=b\)

negative \(y\) when \(y=c\) and positive \(y\) when \(y=d\)

negative \(z\) when \(z=e\) and positive \(z\) when \(z=f\)

Further, the value of \(dy\,dz\) for each parametrization is found from the equation \[ d\vec S=\vec N\,du\,dv=(dy\,dz,dz\,dx,dx\,dy) \] Since \(dy\,dz=0\) for \(4\) of the \(6\) surfaces, the only surfaces that contribute to the right side of Gauss' Theorem are surfaces \(\vec R_1(u,v)\) and \(\vec R_2(u,v)\). Thus we evaluate the right side by summing the two surface integrals: \[\begin{aligned} \iint_{\partial V} P\,dy\,dz &=\iint_{\vec R_1 } P\,dy\,dz+\iint_{\vec R_2 } P\,dy\,dz \\ &=-\int_c^d\int_e^f P(a,v,u)\,du\,dv+\int_e^f\int_c^d P(b,u,v)\,du\,dv \end{aligned}\] Notice that on the surface \(\vec R_1\) the \(u\) variable is the value of \(z\) so that \(e \le u \le f\) and on the surface \(\vec R_2\) the \(u\) variable is the value of \(y\) so that \(c \le u \le d\) and the opposite is true for \(v\).

By Fubini's theorem, we can interchange the order of the differentials of integration on the first integral if we also interchange the order of the limits on the integrals \[ \iint_{\partial V} P\,dy\,dz =-\int_e^f\int_c^d P(a,v,u)\,dv\,du+\int_e^f\int_c^d P(b,u,v)\,du\,dv \] Finally, in the first integral, we replace the dummy variables \(v\) and \(u\) by \(y\) and \(z\) respectively and in the second integral, we replace the dummy variables \(u\) and \(v\) by \(y\) and \(z\) respectively: \[ \iint_{\partial V} P\,dy\,dz =-\int_e^f\int_c^d P(a,y,z)\,dy\,dz+\int_e^f\int_c^d P(b,y,z)\,dy\,dz \] This is the same result we found on the left side. So the theorem is proved for the case that \(\vec F=\langle P,0,0\rangle\). Totally analogous proofs work for the other two cases \(\vec F=\langle 0,Q,0\rangle\) and \(\vec F=\langle 0,0,T\rangle\). They are assigned as exercises. The general result is then just the sum of the three special cases.