22. Parametric Surfaces and Surface Integrals
f. Applications of Vector Surface Integrals
1. Flux and Expansion
The flux of a vector field \(\vec{F}\) through a surface, \(S\), parametrized by \(\vec R(u,v)\) is \[ \iint_S \vec{F}\cdot\vec{dS} =\iint_S \vec{F}(\vec R(u,v))\cdot\vec{N}\,du\,dv \] Note that the notation \(\vec{F}(\vec R(u,v))\) means the vector field \(\vec{F}\) must be evaluated on the surface.
Flux is often used in subjects such as electromagnetism and fluid dynamics. Electric fields, magnetic fields, and fluid flows can be expressed as vector fields, and it is often useful to know how much of one of these fields is flowing through a surface.
The expansion of a vector field \(\vec{F}\) is the flux of the vector field outward through a closed surface (for example, a sphere, box, or a cylinder with the ends closed). The contraction of a vector field \(\vec{F}\) is the negative of the expansion.
See a previous page for a discussion of the orientation of the surface. So to say the surface is oriented outward means the normal is pointing outward.
Find the flux of the velocity field, \(\vec{V}=\left\langle 2xz,2yz,x^2+y^2\right\rangle\), through the paraboloid, \(P\), given by \(z=\dfrac{x^2+y^2}{5}\) for \(z \le 5\) with the normal pointing down and out.
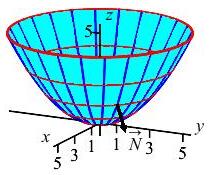
The flux is \(\displaystyle \iint_P \vec{V}\cdot\,d\vec{S}\). In a previous exercies we found the parametrization and normal vector are: \[\begin{aligned} \vec R(r,\theta)&=\left\langle r\cos\theta,r\sin\theta,\dfrac{r^2}{5}\right\rangle \\ \vec N&=\left\langle -\,\dfrac{2r^2}{5}\cos\theta, -\,\dfrac{2r^2}{5}\sin\theta,r\right\rangle \\ \end{aligned}\] The problem requires the normal to be down and out. However,\(r \ge 0\) so that the \(z\)-component of \(\vec N\) is positive, which is up. Further, in the first quadrant, \(\sin\theta \ge 0\) and \(\cos\theta \ge 0\) so that the \(x\)- and \(y\)-components of \(\vec N\) are negative or inward. So we need to reverse \(\vec{N}\): \[ \text{Reverse:}\qquad\vec{N}=\left\langle \dfrac{2r^2}{5}\cos\theta, \dfrac{2r^2}{5}\sin\theta,-r\right\rangle \] Notice, we reverse the entire vector. Next, we evaluate the vector field, \(\vec{V}=\left\langle 2xz,2yz,x^2+y^2\right\rangle\), on the surface: \[ \left.\vec{V}\right|_{\vec R(r,\theta)} =\left\langle \dfrac{2r^3}{5}\cos\theta,\dfrac{2r^3}{5}\sin\theta,r^2\right\rangle \] and compute its dot product with the normal: \[\begin{aligned} \vec{V}\cdot\vec{N} &=\left\langle \dfrac{2r^3}{5}\cos\theta,\dfrac{2r^3}{5}\sin\theta,r^2\right\rangle \cdot\left\langle \dfrac{2r^2}{5}\cos\theta, \dfrac{2r^2}{5}\sin\theta,-r\right\rangle \\ &=\dfrac{4r^5}{25}-r^3 \end{aligned}\] Our integral is \[\begin{aligned} \text{Flux} &=\iint \vec{V}\cdot\vec{N}\,dr\,d\theta =\int_0^{2\pi}\int_0^5 \left(\dfrac{4r^5}{25}-r^3\right)\,dr\,d\theta \\ &=2\pi\left[\dfrac{2r^6}{75}-\dfrac{r^4}{4}\right]_0^5 =2\pi\left(\dfrac{2}{3}5^4-\dfrac{1}{4}5^4\right) =\dfrac{3125}{6}\pi \end{aligned}\]
Caution: Do not put an extra factor of \(r\) into the integrand, just because you see a \(dr\,d\theta\). This \(r\) is already in \(\vec{N}\). While these variables are similar to those used in cylindrical coordinates, they are not the same. Here, \(r\) and \(\theta\) are parameters for the surface, not cylindrical (nor polar) coordinates.
The electric field of a positive point charge is given by: \[\begin{aligned} &\vec E(x,y,z)=\dfrac{\hat r}{r^2}=\dfrac{\vec r}{r^3} \\ &=\left\langle \dfrac{x}{\left(x^2+y^2+z^2\right)^{3/2}}, \dfrac{y}{\left(x^2+y^2+z^2\right)^{3/2}}, \dfrac{z}{\left(x^2+y^2+z^2\right)^{3/2}}\right\rangle \end{aligned}\]
-
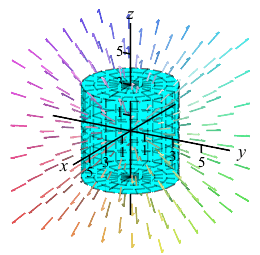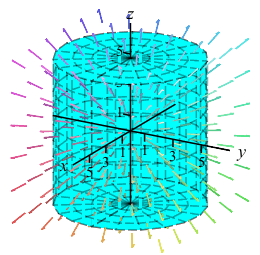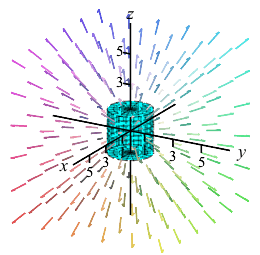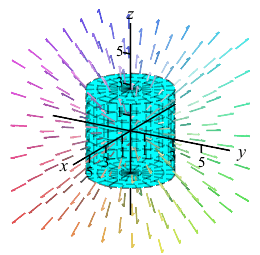
Find the expansion of the electric field out of the total surface of the cylinder, \(C\), given by \(x^2+y^2 \le 9\) and \(-3 \le z \le 3\).
There are \(3\) pieces to the boundary: the curved sides, \(S\), the top, \(T\), and the bottom, \(B\). Compute the flux through each and add them up. To parametrize each surface, start with cylindrical coordinates and set \(r=3\) for the sides, \(z=3\) for the top and \(z=-3\) for the bottom.
\(\displaystyle \text{Expansion}=\iint_C \vec E\cdot d\vec S=4\pi\)
There are \(3\) pieces to the boundary: the curved sides, \(S\), the top, \(T\), and the bottom, \(B\). We will compute the flux through each and add them up.
Sides: \(\displaystyle \text{Flux}_S=\iint_S \vec E\cdot d\vec S\)
\(\displaystyle \text{Flux}_S=\iint_S \vec E\cdot d\vec S=2\pi\sqrt{2}\)
To parametrize the curved side surface, we start with cylindrical coordinates: \[ \vec R(r,\theta,z) =\left\langle r\cos\theta,r\sin\theta,z\right\rangle \] and set \(r=3\): \[ \vec R(\theta,z) =\left\langle 3\cos\theta,3\sin\theta,z\right\rangle \] The tangent and normal vectors are: \[\begin{aligned} \vec e_\theta&=\left\langle -3\sin\theta,3\cos\theta,0\right\rangle \\ \vec e_z&=\left\langle 0,0,1\right\rangle \\ \vec N&=\left\langle 3\cos\theta,3\sin\theta,0\right\rangle \end{aligned}\] As should be expected, the normal is horizontal and the \(x\) and \(y\) components are parallel to those for the position vector. Like the position vector, the normal points outward, as required.
On the surface, the electric field becomes: \[ \vec E(\theta,z) =\left\langle \dfrac{3\cos\theta}{\left(9+z^2\right)^{3/2}}, \dfrac{3\sin\theta}{\left(9+z^2\right)^{3/2}}, \dfrac{z}{\left(9+z^2\right)^{3/2}}\right\rangle \] and its dot product with the normal is: \[ \vec E\cdot\vec N =\dfrac{9\cos^2\theta}{\left(9+z^2\right)^{3/2}} +\dfrac{9\sin^2\theta}{\left(9+z^2\right)^{3/2}} =\dfrac{9}{\left(9+z^2\right)^{3/2}} \] So the flux is: \[\begin{aligned} \text{Flux}_S &=\iint_S \vec E\cdot d\vec S =\iint_S \vec E\cdot \vec N\,d\theta\,dz \\ &=\int_{-3}^3\int_0^{2\pi} \dfrac{9}{\left(9+z^2\right)^{3/2}}\,d\theta\,dz =2\pi\int_{-3}^3 \dfrac{9}{\left(9+z^2\right)^{3/2}}\,dz \end{aligned}\] At this point we use the trig substitution \(z=3\tan\alpha\) and \(dz=3\sec^2\alpha\,d\alpha\): \[\begin{aligned} \text{Flux}_S &=2\pi\int_{z=-3}^{3} \dfrac{9}{\left(9+9\tan^2\alpha\right)^{3/2}}3\sec^2\alpha\,d\alpha \\ &=2\pi\int_{z=-3}^{3} \dfrac{1}{\left(1+\tan^2\alpha\right)^{3/2}}\sec^2\alpha\,d\alpha \\ &=2\pi\int_{z=-3}^{3} \cos\alpha\,d\alpha =2\pi\left[\sin\alpha\dfrac{}{}\right]_{z=-3}^{3} \end{aligned}\] We now draw a right triangle with angle \(\alpha\), opposite side \(z\), adjacent side \(3\) and hypotenuse \(\sqrt{9+z^2}\). Then \(\sin\alpha=\dfrac{z}{\sqrt{9+z^2}}\). So \[\begin{aligned} \text{Flux}_S &=2\pi\left[\dfrac{z}{\sqrt{9+z^2}}\right]_{z=-3}^{3} =4\pi\dfrac{3}{\sqrt{18}} =2\pi\sqrt{2} \end{aligned}\]
Top: \(\displaystyle \text{Flux}_T=\iint_T \vec E\cdot d\vec S\)
\(\displaystyle \text{Flux}_T=\iint_T \vec E\cdot d\vec S=2\pi-\pi\sqrt{2}\)
To parametrize the top surface, we start with cylindrical coordinates and set \(z=3\): \[ \vec R(r,\theta) =\left\langle r\cos\theta,r\sin\theta,3\right\rangle \] After finding the tangent vectors, the normal vector is \(\vec N=\left\langle 0,0,r\right\rangle\). Since the \(z\) component is positive, this points up as required.
On the surface, the electric field becomes: \[ \vec E(\theta,z) =\left\langle \dfrac{r\cos\theta}{\left(r^2+9\right)^{3/2}}, \dfrac{r\sin\theta}{\left(r^2+9\right)^{3/2}}, \dfrac{3}{\left(r^2+9\right)^{3/2}}\right\rangle \] and its dot product with the normal is: \[ \vec E\cdot\vec N =\dfrac{3r}{\left(r^2+9\right)^{3/2}} \] So the flux is: \[\begin{aligned} \text{Flux}_T &=\iint_T \vec E\cdot d\vec S =\iint_T \vec E\cdot \vec N\,dr\,d\theta \\ &=\int_0^{2\pi}\int_0^3 \dfrac{3r}{\left(r^2+9\right)^{3/2}}\,dr\,d\theta =2\pi\int_0^3 \dfrac{3r}{\left(r^2+9\right)^{3/2}}\,dr \end{aligned}\] At this point we use the substitution \(u=r^2+9\) and \(du=2r\,dr\): \[\begin{aligned} \text{Flux}_T &=\pi\int_{r=0}^3 \dfrac{3}{u^{3/2}}\,du =\pi\left[-2\dfrac{3}{u^{1/2}}\right]_{r=0}^3 =-2\pi\left[\dfrac{3}{\left(r^2+9\right)^{1/2}}\right]_0^3 \\ &=-\dfrac{2\pi 3}{\left(18\right)^{1/2}} +\dfrac{2\pi 3}{\left(9\right)^{1/2}} =2\pi-\pi\sqrt{2} \end{aligned}\]
Bottom: \(\displaystyle \text{Flux}_B=\iint_B \vec E\cdot d\vec S\)
\(\displaystyle \text{Flux}_B=\iint_B \vec E\cdot d\vec S=2\pi-\pi\sqrt{2}\)
To parametrize the bottom surface, we start with cylindrical coordinates and set \(z=-3\): \[ \vec R(r,\theta) =\left\langle r\cos\theta,r\sin\theta,-3\right\rangle \] After finding the tangent vectors, the normal vector is \(\vec N=\left\langle 0,0,r\right\rangle\). Since the \(z\) component is positive, this points up but we need it to point down to be out from the solid cylinder. So we reverse it: \[ \text{Reverse:}\qquad\vec N =\left\langle 0,0,-r\right\rangle \]
On the surface, the electric field becomes: \[ \vec E(\theta,z) =\left\langle \dfrac{r\cos\theta}{\left(r^2+9\right)^{3/2}}, \dfrac{r\sin\theta}{\left(r^2+9\right)^{3/2}}, \dfrac{-3}{\left(r^2+9\right)^{3/2}}\right\rangle \] and its dot product with the normal is (again): \[ \vec E\cdot\vec N =\dfrac{3r}{\left(r^2+9\right)^{3/2}} \] So the flux is (again): \[\begin{aligned} \text{Flux}_B &=\iint_B \vec E\cdot d\vec S =\iint_B \vec E\cdot \vec N\,dr\,d\theta \\ &=\int_0^{2\pi}\int_0^3 \dfrac{3r}{\left(r^2+9\right)^{3/2}}\,dr\,d\theta \\ &=\cdots=2\pi-\pi\sqrt{2} \end{aligned}\]
Finally, we add up the flux through the \(3\) surfaces to get the expansion out of the cylinder: \[\begin{aligned} \text{Expansion}&=\iint_C \vec E\cdot d\vec S =\text{Flux}_S+\text{Flux}_T+\text{Flux}_B \\ &=\iint_S \vec E\cdot d\vec S+\iint_T \vec E\cdot d\vec S +\iint_B \vec E\cdot d\vec S \\ &=(2\pi\sqrt{2}) +(2\pi-\pi\sqrt{2}) +(2\pi-\pi\sqrt{2}) =4\pi \end{aligned}\]
-
Find the expansion of the electric field out of the total surface of the cylinder, \(C\), given by \(x^2+y^2 \le R^2\) and \(-H \le z \le H\).
Note: The plot shows the cylinder for various sizes, but only for \(R=H\).\(\displaystyle \text{Expansion}=\iint_C \vec E\cdot d\vec S=4\pi\)
There are \(3\) pieces to the boundary: the curved sides, \(S\), the top, \(T\), and the bottom, \(B\). We will compute the flux through each and add them up.
Sides: \(\displaystyle \text{Flux}_S=\iint_S \vec E\cdot d\vec S\)
\(\displaystyle \text{Flux}_S=\iint_S \vec E\cdot d\vec S=\dfrac{4\pi H}{\sqrt{R^2+H^2}}\)
To parametrize the curved side surface, we start with cylindrical coordinates: \[ \vec R(r,\theta,z) =\left\langle r\cos\theta,r\sin\theta,z\right\rangle \] and set \(r=R\): \[ \vec R(\theta,z) =\left\langle R\cos\theta,R\sin\theta,z\right\rangle \] The tangent and normal vectors are: \[\begin{aligned} \vec e_\theta&=\left\langle -R\sin\theta,R\cos\theta,0\right\rangle \\ \vec e_z&=\left\langle 0,0,1\right\rangle \\ \vec N&=\left\langle R\cos\theta,R\sin\theta,0\right\rangle \end{aligned}\] As should be expected, the normal is horizontal and the \(x\) and \(y\) components are parallel to those for the position vector. Like the position vector, the normal points outward, as required.
On the surface, the electric field becomes: \[ \vec E(\theta,z) =\left\langle \dfrac{R\cos\theta}{\left(R^2+z^2\right)^{3/2}}, \dfrac{R\sin\theta}{\left(R^2+z^2\right)^{3/2}}, \dfrac{z}{\left(R^2+z^2\right)^{3/2}}\right\rangle \] and its dot product with the normal is: \[ \vec E\cdot\vec N =\dfrac{R^2\cos^2\theta}{\left(R^2+z^2\right)^{3/2}} +\dfrac{R^2\sin^2\theta}{\left(R^2+z^2\right)^{3/2}} =\dfrac{R^2}{\left(R^2+z^2\right)^{3/2}} \] So the flux is: \[\begin{aligned} \text{Flux}_S &=\iint_S \vec E\cdot d\vec S =\iint_S \vec E\cdot \vec N\,d\theta\,dz \\ &=\int_{-H}^H\int_0^{2\pi} \dfrac{R^2}{\left(R^2+z^2\right)^{3/2}}\,d\theta\,dz =2\pi\int_{-H}^H \dfrac{R^2}{\left(R^2+z^2\right)^{3/2}}\,dz \end{aligned}\] At this point we use the trig substitution \(z=R\tan\alpha\) and \(dz=R\sec^2\alpha\,d\alpha\): \[\begin{aligned} \text{Flux}_S &=2\pi\int_{z=-H}^{H} \dfrac{R^2}{\left(R^2+R^2\tan^2\alpha\right)^{3/2}}R\sec^2\alpha\,d\alpha \\ &=2\pi\int_{z=-H}^{H} \dfrac{1}{\left(1+\tan^2\alpha\right)^{3/2}}\sec^2\alpha\,d\alpha \\ &=2\pi\int_{z=-H}^{H} \cos\alpha\,d\alpha =2\pi\left[\sin\alpha\dfrac{}{}\right]_{z=-H}^{H} \end{aligned}\] We now draw a right triangle with angle \(\alpha\), opposite side \(z\), adjacent side \(R\) and hypotenuse \(\sqrt{R^2+z^2}\). Then \(\sin\alpha=\dfrac{z}{\sqrt{R^2+z^2}}\). So \[\begin{aligned} \text{Flux}_S &=2\pi\left[\dfrac{z}{\sqrt{R^2+z^2}}\right]_{z=-H}^{H} =\dfrac{4\pi H}{\sqrt{R^2+H^2}} \end{aligned}\]
Top: \(\displaystyle \text{Flux}_T=\iint_T \vec E\cdot d\vec S\)
\(\displaystyle \text{Flux}_T=\iint_T \vec E\cdot d\vec S =2\pi-\dfrac{2\pi H}{\sqrt{R^2+H^2}}\)
To parametrize the top surface, we start with cylindrical coordinates and set \(z=H\): \[ \vec R(r,\theta) =\left\langle r\cos\theta,r\sin\theta,H\right\rangle \] After finding the tangent vectors, the normal vector is \(\vec N=\left\langle 0,0,r\right\rangle\). Since the \(z\) component is positive, this points up as required.
On the surface, the electric field becomes: \[ \vec E(\theta,z) =\left\langle \dfrac{r\cos\theta}{\left(r^2+H^2\right)^{3/2}}, \dfrac{r\sin\theta}{\left(r^2+H^2\right)^{3/2}}, \dfrac{H}{\left(r^2+H^2\right)^{3/2}}\right\rangle \] and its dot product with the normal is: \[ \vec E\cdot\vec N =\dfrac{Hr}{\left(r^2+H^2\right)^{3/2}} \] So the flux is: \[\begin{aligned} \text{Flux}_T &=\iint_T \vec E\cdot d\vec S =\iint_T \vec E\cdot \vec N\,dr\,d\theta \\ &=\int_0^{2\pi}\int_0^R \dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}\,dr\,d\theta =2\pi\int_0^R \dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}\,dr \end{aligned}\] At this point we use the substitution \(u=r^2+H^2\) and \(du=2r\,dr\): \[\begin{aligned} \text{Flux}_T &=\pi\int_{r=0}^R \dfrac{H}{u^{3/2}}\,du =\pi\left[-2\dfrac{H}{u^{1/2}}\right]_{r=0}^R =-2\pi\left[\dfrac{H}{\left(r^2+H^2\right)^{1/2}}\right]_0^R \\ &=-\dfrac{2\pi H}{\left(R^2+H^2\right)^{1/2}} +\dfrac{2\pi H}{\left(H^2\right)^{1/2}} =2\pi-\dfrac{2\pi H}{\sqrt{R^2+H^2}} \end{aligned}\]
Bottom: \(\displaystyle \text{Flux}_B=\iint_B \vec E\cdot d\vec S\)
\(\displaystyle \text{Flux}_B=\iint_B \vec E\cdot d\vec S =2\pi-\dfrac{2\pi H}{\sqrt{R^2+H^2}}\)
To parametrize the bottom surface, we start with cylindrical coordinates and set \(z=-H\): \[ \vec R(r,\theta) =\left\langle r\cos\theta,r\sin\theta,-H\right\rangle \] After finding the tangent vectors, the normal vector is \(\vec N=\left\langle 0,0,r\right\rangle\). Since the \(z\) component is positive, this points up but we need it to point down to be out from the solid cylinder. So we reverse it: \[ \text{Reverse:}\qquad\vec N =\left\langle 0,0,-r\right\rangle \]
On the surface, the electric field becomes: \[ \vec E(\theta,z) =\left\langle \dfrac{r\cos\theta}{\left(r^2+H^2\right)^{3/2}}, \dfrac{r\sin\theta}{\left(r^2+H^2\right)^{3/2}}, \dfrac{-H}{\left(r^2+H^2\right)^{3/2}}\right\rangle \] and its dot product with the normal is (again): \[ \vec E\cdot\vec N =\dfrac{Hr}{\left(r^2+H^2\right)^{3/2}} \] So the flux is (again): \[\begin{aligned} \text{Flux}_B &=\iint_B \vec E\cdot d\vec S =\iint_B \vec E\cdot \vec N\,dr\,d\theta \\ &=\int_0^{2\pi}\int_0^R \dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}\,dr\,d\theta \\ &=\cdots=2\pi-\dfrac{2\pi H}{\sqrt{R^2+H^2}} \end{aligned}\]
Finally, we add up the flux through the \(3\) surfaces to get the expansion out of the cylinder: \[\begin{aligned} \text{Expansion}&=\iint_C \vec E\cdot d\vec S =\text{Flux}_S+\text{Flux}_T+\text{Flux}_B \\ &=\iint_S \vec E\cdot d\vec S+\iint_T \vec E\cdot d\vec S +\iint_B \vec E\cdot d\vec S \\ &=\left(\dfrac{4\pi H}{\sqrt{R^2+H^2}}\right) +\left(2\pi-\dfrac{2\pi H}{\sqrt{R^2+H^2}}\right) +\left(2\pi-\dfrac{2\pi H}{\sqrt{R^2+H^2}}\right) \\ &=4\pi \end{aligned}\]
-
Compare the expansion for various values of \(R\) and \(H\). Does the expansion get larger or smaller as \(R\) or \(H\) gets bigger.
The expansion is independent of \(R\) and \(H\).
The expansion, \(\displaystyle \iint_C \vec E\cdot d\vec S=4\pi\), independent of \(R\) and \(H\).
In a later chapter, we will learn that Gauss' Theorem says this integral is surface independent. Consequently, changing the values of \(R\) and \(H\) does not change the value of the integral.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum