22. Parametric Surfaces and Surface Integrals
e. Vector Surface Integrals
Recall that for a curve \(\vec r(t)=\left\langle x(t),y(t),z(t)\right\rangle\), the tangent vector is \(\vec v(t) =\left\langle \dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\) and the vector differential is: \[ d\vec{s}=\vec{v}\,dt =\left\langle \dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt \] We frequently cancel the \(dt\)'s and write simply: \[ d\vec{s}=\vec{v}\,dt=\left\langle dx,dy,dz\right\rangle \] Then the line integral of a vector \(\vec F=\left\langle F_1,F_2,F_3\right\rangle\) is \[ \int_A^B \vec{F}\cdot\,d\vec{s} =\int_A^B F_1\,dx+F_2\,dy+F_3\,dz \] When we use this form of the integral, we need to remember to evaluate \(F_1\), \(F_2\) and \(F_3\) at \((x(t),y(t),z(t))\) and to substitute the differentials \(dx=\dfrac{dx}{dt}\,dt\), \(dy=\dfrac{dy}{dt}\,dt\) and \(dz=\dfrac{dz}{dt}\,dt\).
For an example, see the second example on the page on Line Integrals of Vectors
3. Alternate Notations
Similarly, for a surface \(\vec R(u,v)=\left\langle x(u,v),y(u,v),z(u,v)\right\rangle\), the normal vector \(\vec{N}=\vec{e}_u\times\vec{e}_v\) can be written as: \[\begin{aligned} \vec{N} &=\left\langle \dfrac{\partial(y,z)}{\partial(u,v)}, -\,\dfrac{\partial(x,z)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle \\ &=\left\langle \dfrac{\partial(y,z)}{\partial(u,v)}, \dfrac{\partial(z,x)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle \end{aligned}\] where the terms are \(2\) dimensional Jacobian determinants. In the second version, we have absorbed the minus (\(-\)) sign into the second determinant by reversing the columns from \((x,z)\) to \((z,x)\).
Substituting the first version of \(\vec N\) into \(d\vec{S}=\vec{N}\,du\,dv\), we get: \[ d\vec{S} =\left\langle \dfrac{\partial(y,z)}{\partial(u,v)}, -\,\dfrac{\partial(x,z)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle\,du\,dv \] Like cancelling \(dt\)'s, we sometimes cancel the \(\partial(u,v)\) in the bottom of each Jacobian with the \(du\,dv\) terms that are outside the parentheses. This results in the expression: \[ d\vec{S}=\left\langle dy\,dz,-dx\,dz,dx\,dy\right\rangle \] where in the above expression, the products of differentials mean \[\begin{aligned} dy\,dz=\dfrac{\partial(y,z)}{\partial(u,v)}\,du\,dv \qquad dx\,dz=\dfrac{\partial(x,z)}{\partial(u,v)}\,du\,dv \qquad dx\,dy=\dfrac{\partial(x,y)}{\partial(u,v)}\,du\,dv \end{aligned}\]
Similarly, substituting the second version of \(\vec N\) into \(d\vec{S}=\vec{N}\,du\,dv\), we get: \[\begin{aligned} d\vec{S} &=\left\langle \dfrac{\partial(y,z)}{\partial(u,v)}, \dfrac{\partial(z,x)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle\,du\,dv \\ &=\left\langle dy\,dz,dz\,dx,dx\,dy\right\rangle \end{aligned}\] where this time the second product of differentials means \[ dz\,dx=\dfrac{\partial(z,x)}{\partial(u,v)}\,du\,dv \]
Notice that \(\dfrac{\partial(z,x)}{\partial(u,v)}=-\,\dfrac{\partial(x,z)}{\partial(u,v)}\) since they are the same determinant except that the two columns are reversed. Consequently, \(dx\,dz \neq dz\,dx\). Rather, \[ dx\,dz=-dz\,dx \] This is shocking at first but one gets used to it. The expression is similar to a cross product in that interchanging two vectors will result in a minus sign in the cross product. Similarly, when multiplying differentials, interchanging the two, results in a minus sign in the product. The differentials can be written in either order when computing an integral provided the appropriate minus sign is included. In particular, alphabetical order, \(dx\,dz\), needs a minus, while cylic order, \(dz\,dx\) does not.
Using this alternate version of \(d\vec S\), the surface integral of a vector \(\vec F=\left\langle F_1,F_2,F_3\right\rangle\) is \[\begin{aligned} \iint_S \vec{F}\cdot\,d\vec{S} &=\iint_S F_1\,dy\,dz-F_2\,dx\,dz+F_3\,dx\,dy \\ &=\iint_S F_1\,dy\,dz+F_2\,dz\,dx+F_3\,dx\,dy \end{aligned}\] Notice that in the expression with a minus the differentials are in alphabetical order; in the expression with a plus the differentials are in cyclic order. As usual, limits need to be put on the surface integral to describe the boundary.
When we use this form of the integral, we need to remember to evaluate \(F_1\), \(F_2\) and \(F_3\) at \(\vec R(u,v)\) and to substitute for the differentials \(dy\,dz\), \(dx\,dz\) or \(dz\,dx\) and \(dx\,dy\) in terms of Jacobians.
Compute \(\displaystyle \iint_P xz^2\,dy\,dz-yz^2\,dx\,dz-2z^3\,dx\,dy\) over the piece of the paraboloid \(z=\dfrac{x^2+y^2}{5}\) below \(z=5\) orientated with the normal pointing down and out from the paraboloid.
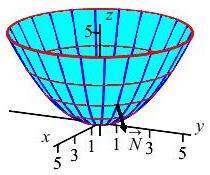
The paraboloid may be parametrized by: \[ x=r\cos\theta \qquad y=r\sin\theta \qquad z=\dfrac{r^2}{5} \] The differentials are: \[\begin{aligned} dy\,dz&=\dfrac{\partial(y,z)}{\partial(r,\theta)}\,dr\,d\theta =\left(\dfrac{\partial y}{\partial r}\dfrac{\partial z}{\partial \theta} -\dfrac{\partial z}{\partial r}\dfrac{\partial y}{\partial \theta}\right)\,dr\,d\theta \\ &=(\sin\theta\cdot0-\dfrac{2r}{5}\cdot r\cos\theta)\,dr\,d\theta =-\,\dfrac{2r^2}{5}\cos\theta\,dr\,d\theta \\ dx\,dz&=\dfrac{\partial(x,z)}{\partial(r,\theta)}\,dr\,d\theta =\left(\dfrac{\partial x}{\partial r}\dfrac{\partial z}{\partial \theta} -\dfrac{\partial z}{\partial r}\dfrac{\partial x}{\partial \theta}\right)\,dr\,d\theta \\ &=(\cos\theta\cdot0+\dfrac{2r}{5}\cdot r\sin\theta)\,dr\,d\theta =\dfrac{2r^2}{5}\sin\theta\,dr\,d\theta \\ dx\,dy&=\dfrac{\partial(x,y)}{\partial(r,\theta)}\,dr\,d\theta =\left(\dfrac{\partial x}{\partial r}\dfrac{\partial y}{\partial \theta} -\dfrac{\partial y}{\partial r}\dfrac{\partial x}{\partial \theta}\right)\,dr\,d\theta \\ &=(r\cos^2\theta+r\sin^2\theta)\,dr\,d\theta =r\,dr\,d\theta \\ \end{aligned}\] To check the orientation, we still need to look at the normal or the differential: \[\begin{aligned} d\vec{S}&=\left\langle dy\,dz,-dx\,dz,dx\,dy\right\rangle \\ &=\left\langle -\,\dfrac{2r^2}{5}\cos\theta,-\dfrac{2r^2}{5}\sin\theta,r\right\rangle\,dr\,d\theta \end{aligned}\] Be careful with the minus on the second component! Since the first \(2\) components are negative (in the \(1^\text{st}\) quadrant) and the \(3^\text{rd}\) component is positive, the normal points in and up. Since we need it down and out, we need to reverse it. We do this by reversing the sign of all \(3\) differentials: \[\begin{aligned} dy\,dz=\dfrac{2r^2}{5}\cos\theta&\,dr\,d\theta \qquad dx\,dz=-\,\dfrac{2r}{5}\sin\theta\,dr\,d\theta \\ &dx\,dy=-r\,dr\,d\theta \end{aligned}\] We are ready to compute the integral. We substitute for each coordinate and each differential: \[\begin{aligned} \iint_P &(x)(z)^2(dy\,dz)-(y)(z)^2(dx\,dz)-2(z)^3(dx\,dy) \\ &=\iint_P \left[(r\cos\theta)\left(\dfrac{r^2}{5}\right)^2\left(\dfrac{2r^2}{5}\cos\theta\right)\right. \\ &\quad\left.-(r\sin\theta)\left(\dfrac{r^2}{5}\right)^2\left(-\,\dfrac{2r^2}{5}\sin\theta\right) -2\left(\dfrac{r^2}{5}\right)^3(-r)\right]\,dr\,d\theta \\ &=\int_0^{2\pi}\int_0^5 \left(\dfrac{2r^7}{125}\cos^2\theta+\dfrac{2r^7}{125}\sin^2\theta+\dfrac{2r^7}{125}\right)\,dr\,d\theta \\ &=\int_0^{2\pi}\int_0^5 \dfrac{4r^7}{125}\,dr\,d\theta =2\pi\left[\dfrac{r^8}{250}\right]_0^5 =3125\pi \end{aligned}\]
If we prefer, we can always convert back to the \(\displaystyle \iint_S \vec{F}\cdot\,d\vec{S}\) notation by identifying the components of \(\vec F\) as the coefficients of \(dy\,dz\), \(-dx\,dz\) and \(dx\,dy\). In this example, given the integral \(\displaystyle \iint_P xz^2\,dy\,dz-yz^2\,dx\,dz-2z^3\,dx\,dy\), we identify the vector field as \[ \vec F=\left\langle xz^2,yz^2,-2z^3\right\rangle \] (Be careful with the sign of the \(y\) component.) Notice, this is the same integral as in the exercise on the previous page. In both versions, we need to compute the Jacobians which are the components of the normal. However, to check the orientation in the differentail version, we need to reconstruct the normal anyway. So the first version is probably more direct.
Compute \(\displaystyle \iint_P xz\,dy\,dz+yz\,dz\,dx+z^2\,dx\,dy\) over the polar cap (\(0 \le \phi \le \dfrac{\pi}{6}\)) of a sphere of radius \(2\) with the orientation outward from the sphere.
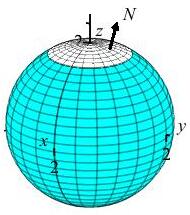
\(\displaystyle \iint_P xz\,dy\,dz+yz\,dz\,dx+z^2\,dx\,dy=4\pi\)
The sphere may be parametrized by: \[ x=2\sin\phi\cos\theta \qquad y=2\sin\phi\sin\theta \qquad z=2\cos\phi \] The differentials are: \[\begin{aligned} dy\,dz&=\dfrac{\partial(y,z)}{\partial(\phi,\theta)}\,d\phi\,d\theta =\left(\dfrac{\partial y}{\partial \phi}\dfrac{\partial z}{\partial \theta} -\dfrac{\partial z}{\partial \phi}\dfrac{\partial y}{\partial \theta}\right)\,d\phi\,d\theta \\ &=(2\cos\phi\sin\theta\cdot0--2\sin\phi\cdot2\sin\phi\cos\theta)\,d\phi\,d\theta \\ &=4\sin^2\phi\cos\theta\,d\phi\,d\theta \\ dz\,dx&=\dfrac{\partial(z,x)}{\partial(\phi,\theta)}\,d\phi\,d\theta =\left(\dfrac{\partial z}{\partial \phi}\dfrac{\partial x}{\partial \theta} -\dfrac{\partial x}{\partial \phi}\dfrac{\partial z}{\partial \theta}\right)\,d\phi\,d\theta \\ &=(--2\sin\phi\cdot2\sin\phi\sin\theta-2\cos\phi\cos\theta\cdot0)\,d\phi\,d\theta \\ &=4\sin^2\phi\sin\theta\,d\phi\,d\theta \\ dx\,dy&=\dfrac{\partial(x,y)}{\partial(\phi,\theta)}\,d\phi\,d\theta =\left(\dfrac{\partial x}{\partial \phi}\dfrac{\partial y}{\partial \theta} -\dfrac{\partial y}{\partial \phi}\dfrac{\partial x}{\partial \theta}\right)\,d\phi\,d\theta \\ &=(2\cos\phi\cos\theta\cdot2\sin\phi\cos\theta \\ &\qquad--2\cos\phi\sin\theta\cdot2\sin\phi\sin\theta)\,d\phi\,d\theta \\ &=4\cos\phi\sin\phi\,d\phi\,d\theta \\ \end{aligned}\] From these differentials we can read off the normal vector: \[ \vec{N}=\left\langle 4\sin^2\phi\cos\theta,4\sin^2\phi\sin\theta, 4\cos\phi\sin\phi\right\rangle \] Since all \(3\) components are positive (in the \(1^\text{st}\) octant), the normal points outward as required. We are ready to compute the integral. We substitute for each coordinate and each differential: \[\begin{aligned} \iint_P &xz\,dy\,dz+yz\,dz\,dx+z^2\,dx\,dy \\ &=\iint_P \left[(2\sin\phi\cos\theta)(2\cos\phi)(4\sin^2\phi\cos\theta)\dfrac{}{}\right. \\ &\qquad\qquad+(2\sin\phi\sin\theta)(2\cos\phi)(4\sin^2\phi\sin\theta) \\ &\qquad\qquad+\left.(2\cos\phi)^2(4\cos\phi\sin\phi)\dfrac{}{}\right]\,d\phi\,d\theta \\ &=16\int_0^{2\pi}\int_0^{\pi/6} (\sin^3\phi\cos\phi+\cos^3\phi\sin\phi)\,d\phi\,d\theta \\ &=16\int_0^{2\pi}\int_0^{\pi/6} \sin\phi\cos\phi\,dr\,d\theta =32\pi\left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/6} =4\pi \end{aligned}\]
Notice, this is the same integral as in the example on the previous page. This time the normal was correctly oriented because we ordered the coordinates as \((\phi,\theta)\) instead of \((\theta,\phi)\). If we did not need to construct the normal to check the orientation, the second method might be faster. But since we do need the normal, the first method is probably more direct. Given the integral \(\displaystyle \iint_P xz\,dy\,dz+yz\,dz\,dx+z^2\,dx\,dy\), we identify the vector field as \(\vec F=\left\langle xz,yz,z^2\right\rangle\) (Be careful with the sign of the \(y\) component.) and proceed to compute the integral \(\displaystyle \iint_P \vec{F}\cdot\,d\vec{S}\).
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum