22. Parametric Surfaces and Surface Integrals

Homework

This Homework will be handed out. It will include the following two problems.

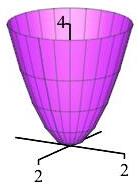
1. Consider the piece of the paraboloid \(z=x^2+y^2\) below \(z=4\). Assume the paraboloid is oriented down and out and has density \(\delta=x^2+y^2\). Also consider the vector field \(\vec{G}=\langle x,y,xz+yz\rangle\).

   

   1. Parameterize the paraboloid starting from cylindrical coordinates.

   2. Find the tangent vectors to the paraboloid and find a parametric equation for the tangent plane to the paraboloid at the point \((r,\theta)=(1,\pi)\).

   3. Find the normal vector to the paraboloid and check its orientation. Then find the normal equation for the tangent plane to the paraboloid at the point \((r,\theta)=(1,\pi)\).

   4. Find the length of the normal and the area of the paraboloid.

   5. Find the centroid of the paraboloid.

   6. Find the mass of the paraboloid.

   7. Find the center of mass of the paraboloid.

   8. Find the average density of the paraboloid.

   9. Evaluate the vector field \(\vec G\) on the paraboloid.

   10. Compute \(\displaystyle \iint_P\vec{G}\cdot\,d\vec{S}\) over the piece of the paraboloid with \(r \le 2\) .

2. Compute \(\displaystyle \iint_H \vec\nabla \times\vec F\cdot d\vec S\) for the vector field \(\vec F=\langle yz,-xz,z^2\rangle\) over the hemisphere \(x^2+y^2+z^2=9\) for \(z \ge 0\) oriented up and out.