17. Divergence, Curl and Potentials
d. Differential Identities
2. Second Order Differential Operators and Identities
a. The Divergence of a Gradient (\(\vec\nabla\cdot\vec\nabla f\)) - The Laplacian
This requires a definition.
The Laplacian of a scalar field \(f\) is the scalar field \[\begin{aligned} \text{Lap}f &=\nabla^2f=\vec\nabla\cdot\vec\nabla f \\ &=\dfrac{\partial^2 f}{\partial x^2} +\dfrac{\partial^2 f}{\partial y^2} +\dfrac{\partial^2 f}{\partial z^2} \end{aligned}\]
The gradient is \(\vec\nabla f=\left\langle \partial_x f, \partial_y f, \partial_z f\right\rangle\). So the divergence of the gradient is \[ \vec\nabla\cdot\vec\nabla f =\left\langle \partial_x, \partial_y, \partial_z\right\rangle\cdot \left\langle \partial_x f, \partial_y f, \partial_z f\right\rangle =\partial_x^2 f +\partial_y^2 f +\partial_z^2 f \]
Compute the Laplacian of the function \(f=x^2y^3+y^2z^3\).
The gradient of \(f\) is \[ \vec\nabla f=\left\langle 2xy^3, 3x^2y^2+2yz^3, 3y^2z^2\right\rangle \] The Laplacian is \[\begin{aligned} \nabla^2f &=\vec\nabla\cdot\vec\nabla f \\ &=\dfrac{\partial}{\partial x}(2xy^3) +\dfrac{\partial}{\partial y}(3x^2y^2+2yz^3) +\dfrac{\partial}{\partial z}(3y^2z^2) \\ &=2y^3+6x^2y+2z^3+6y^2z \end{aligned}\] Note the answer is a scalar field, as it only has one function.
The Laplacian occurs in many differential equations. Here are some famous ones:
The Laplace Equation is: \[ \nabla^2f=0 \] Any solution of the Laplace equation is called an harmonic function.
The Poisson Equation is: \[ \nabla^2f=\rho \] where \(\rho\) is a given function called the source.
The Laplacian also occurs in the differential equation version of many laws of physics.
If the temperature of an object depends on both position and time, then the temperature is a function of the space coordinates \(x\), \(y\) and \(z\) as well as time \(t\). Then the temperature \(T=T(t,x,y,z)\) satisfies the Heat Equation: \[ \dfrac{\partial T}{\partial t}=k \nabla^2T \] where \(k\) is the heat flow constant of the material of the object.
There are many types of waves: the vibration of a string or a drum head or the air in a tube, a sound wave or an electromagnetic wave. These all satisfy the Wave Equation: \[ \dfrac{\partial^2 f}{\partial t^2}-v^2 \nabla^2f=0 \] where \(v\) is the velocity of the wave.
The gravitational potential \(\phi_g\) is a solution of Newton's Law of Gravity which is the Poisson equation: \[ \nabla^2\phi_g=4\pi\rho_g \] where \(\rho_g\) is is the mass density. In empty space, this reduces to the Laplace equation.
The electrostatics potential \(\phi_e\) is a solution of Coulomb's Law of Electrostatics which is the Poisson equation: \[ \nabla^2\phi_e=4\pi\rho_e \] where \(\rho_e\) is is the charge density. In empty space, this reduces to the Laplace equation.
You will have to wait until a course in partial differential equations to learn how to solve these equations. But you can already verify that a given function satisfies an equation.
Verify that the function \[ f(t,x)=2\sin(x+vt)+3\cos(x-vt) \] satisfies the (\(1\)-dimensional) wave equation.
Compute \(\partial^2_t f\) and \(\nabla^2f=\partial^2_x f\) and substitute into the left side of the Wave Equation to get \(0\).
We compute the first and second derivatives: \[\begin{aligned} \partial_t f&=2v\cos(x+vt)+3v\sin(x-vt) \\ \partial^2_t f&=-2v^2\sin(x+vt)-3v^2\cos(x-vt) \\[6pt] \partial_x f&=2\cos(x+vt)-3\sin(x-vt) \\ \nabla^2f=\partial^2_x f&=-2\sin(x+vt)-3\cos(x-vt) \end{aligned}\] Then we plug them into the left side of the wave equation: \[\begin{aligned} \partial^2_t f-v^2\nabla^2f &=-2v^2\sin(x+vt)-3v^2\cos(x-vt) \\ &\quad-v^2(-2\sin(x+vt)-3\cos(x-vt))=0 \end{aligned}\]
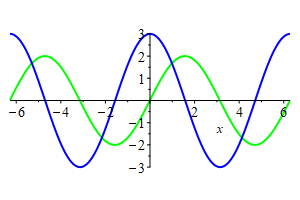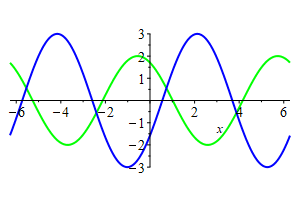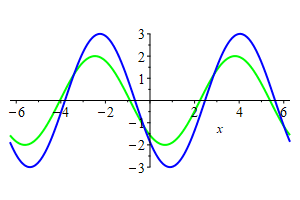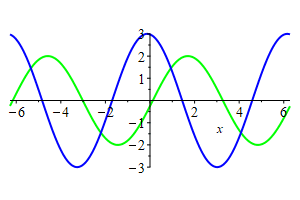
The plot at the right shows the graphs of
\(2\sin(x+2t)\) shown in green, which is a wave moving left,
\(3\cos(x-2t)\) shown in blue, which is a wave moving right.
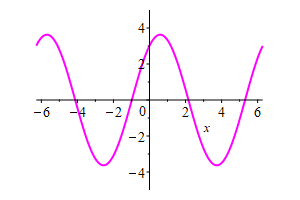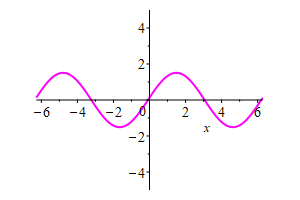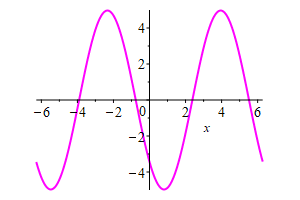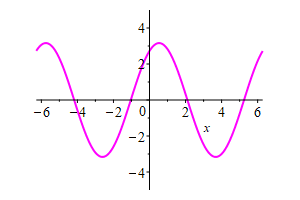
The plot at the right shows the sum
\(2\sin(x+2t)+3\cos(x-2t)\) shown in magenta.
In fact, any function of the form: \[ f(x,t)=g(x+vt)+h(x-vt) \] for any functions \(g\) and \(h\) will satisfy the \(1\)-dimensional wave equation: \[ \partial^2_t f-v^2\partial^2_x f=0 \] because, by the chain rule: \[ \partial^2_t f=v^2g''(x+vt)+v^2h''(x-vt) \] while: \[ \partial^2_x f=g''(x+vt)+h''(x-vt) \] The function \(g(x+vt)\) describes a wave traveling to the left, while the function \(h(x-vt)\) describes a wave traveling to the right.