13. Volume

e1a. Volume using Thin Cylinders - Example

The area below the function \(y=3\sin x\) between \(x=0\) and \(x=\pi\) is rotated about the \(y\)-axis producing a solid of revolution shaped like a jello mold. Find the volume.

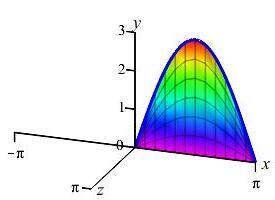
This plot shows the area between the top part of a sine wave and the axis.

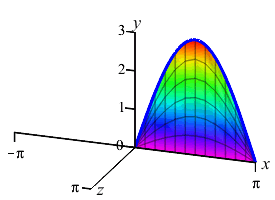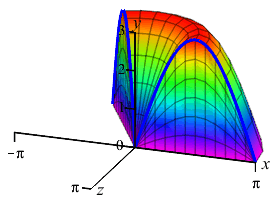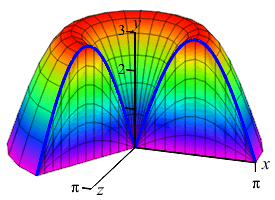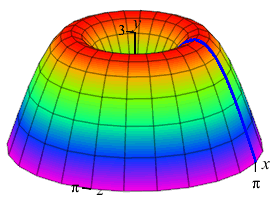
This shows the area rotated about the y axis forming a jello mold.

We do not want to compute the volume as a \(y\) integral because that would require integrals of \(\arcsin\)'s. So we do an \(x\)-integral. The rectangles are vertical and rotate into thin cylinders. The last plot shows the thin cylinders accumulating to form the solid.

The radius is \(x\) and the height is \(3\sin x\). So the volume is \[ V=\int_0^\pi 2\pi x\cdot3\sin x\,dx \]

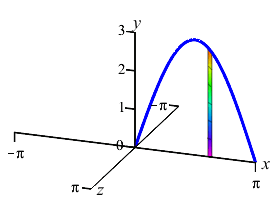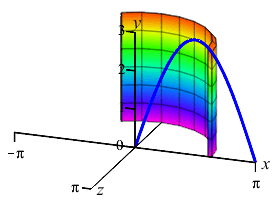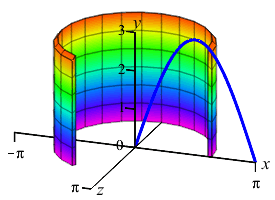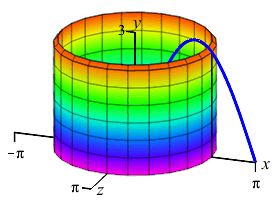
This shows a vertical slice of the region rotating about the y axis,
forming a cylinder.

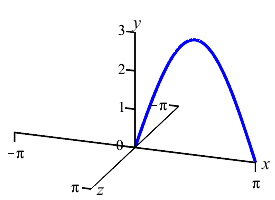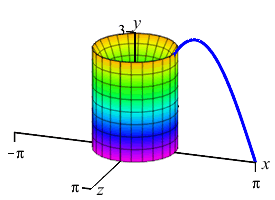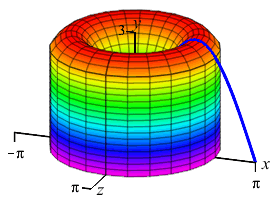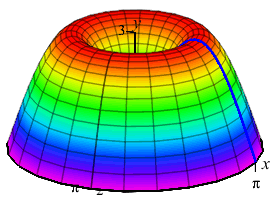
This shows the cylinders accumulating to form a jelly mold like shape.

To do the integral, we must use integration by parts with \[\begin{array}{ll} u=6\pi x & dv=\sin x\,dx \\ du=6\pi\,dx \quad & v=-\cos x \end{array}\] So the volume is: \[\begin{aligned} V&=\left[-6\pi x\cos x+\int 6\pi\cos x\,dx\right]_0^\pi \\ &=\left[-6\pi x\cos x+6\pi\sin x\rule{0pt}{10pt}\right]_0^\pi =-6\pi\pi\cos\pi=6\pi^2 \end{aligned}\]