10. Area and Average Value
d. Average Value and Mean Value Theorem
Recall: The average value of a function \(f(x)\) on an interval \([a,b]\) is: \[ f_\text{ave}=\dfrac{1}{b-a}\int_a^b f(x)\,dx \]
3. Mean Value Theorem for Integrals
Next notice that the average value of a function \(f\) on an interval \([a,b]\) is always between the minimum and maximum values of \(f\) on the interval \([a,b]\).
If \(m\) is the minimum and \(M\) is the maximum, then: \[ m \le f(x) \le M \] \[ \int_a^b m\,dx \le \int_a^b f(x)\,dx \le \int_a^b M\,dx \] \[ m(b-a) \le \int_a^b f(x)\,dx \le M(b-a) \] \[ m \le f_\text{ave} \le M \]
Consequently, by the Intermediate Value Theorem, if \(f(x)\) is continuous on \([a,b]\), then there is a number \(c\) in \([a,b]\) where \(f(c)=f_\text{ave}\). Thus we conclude:
If \(f(x)\) is a continuous function on the interval \([a,b]\), then there is a number \(c\) in \([a,b]\), where: \[ f(c)=f_\text{ave}=\dfrac{1}{b-a}\int_a^b f(x)\,dx \]
The number \(c\) may or may not be unique.
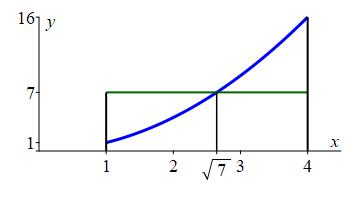
Find the number(s) \(c\) guaranteed by the Mean Value Theorem for Integrals for the function \(f(x)=x^2\) on the interval \([1,4]\).
The average value was found in a previous example to be \(f_\text{ave}=7\). So we need to solve \(f(c)=f_\text{ave}\) or \(c^2=7\). Therefore \(c=\sqrt{7}\). This is the point where the green line crosses the blue curve in the graph:
Notice the solution \(c=-\sqrt{7}\) is not in the interval \([1,4]\).
Your turn:
Find the number(s) \(c\) guaranteed by the Mean Value Theorem for Integrals for the function \(f(x)=(x-2)^2\) on the interval \([1,3]\).
\(c=2\pm\dfrac{1}{\sqrt{3}}\)
The average value was found, in a previous exercise, to be \(f_\text{ave}=\dfrac{1}{3}\). So we need to solve \((c-2)^2=\dfrac{1}{3}\). Therefore \(c_\pm=2\pm\dfrac{1}{\sqrt{3}}\). These are the two points where the green line crosses the blue curve in the graph:
^2_sol.jpg)
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum