21. Antiderivatives, Areas and the FTC

e. Area as an Antiderivative

We know that position and velocity are respectively the antiderivatives of the velocity and acceleration. We will see here that "area" can also be expressed as an antiderivative. To do that, we first need to define the "area" function and then we need to compute its derivative.

Given a positive function \(f(x)\) defined on an interval \([a,b]\), the area under the graph of \(y=f(x)\) above the \(x\)-axis between \(x=a\) and \(x=b\) is denoted by \(A(a,b)\) and called the area under \(f(x)\) above the interval \([a,b]\). To get the area as a function, we fix the left endpoint, \(a\), and let the right endpoint be a variable, \(x\). Thus the area function for \(f(x)\) starting at \(x=a\) is: \[A_a(x)=A(a,x)\]

We can now compute the derivative of the area function, \(A_a(x)\).

If \(A_a(x)\) is the area function for \(f(x)\) starting at \(x=a\), then its derivative is \(f(x)\). That is: \[ \dfrac{d}{dx}A_a(x)=f(x) \] Either read the proof or do the Maplet below.

Throughout the proof, we will write \(A(x)\) instead of \(A_a(x)\).

We wish to find the derivative of the area function, \(A(x)\), shown in magenta.

By definition, the derivative is \[ A'(x)=\lim_{h\to0}\dfrac{A(x+h)-A(x)}{h} \] We start by examining the numerator.

In this plot, \(A(x)\) is shown in magenta, while \(A(x+h)\) is shown in magenta and green together. So the numerator is the difference, \(A(x+h)-A(x)\), which is shown in green alone. Consequently, the quotient is the green area divided by \(h\) and we need to take the limit as the green area goes to zero.

To compute the limit, we approximate the green area, \(A(x+h)-A(x)\), by the blue (and green) rectangle whose height is \(f(x)\) and whose width is \(h\). So the area is approximately: \[ A(x+h)-A(x)\approx f(x)\cdot h \] (This approximation gets better as \(h\) approaches \(0\).) So the quotient is approximately: \[ \dfrac{A(x+h)-A(x)}{h}\approx f(x) \] Notice that this value is independent of \(h\). So the limit is: \[ \lim_{h\to0}\dfrac{A(x+h)-A(x)}{h} =\lim_{h\to0}f(x)=f(x) \] We conclude the derivative of the area function is the original function: \[ A'(x)=f(x) \]

We can make the proof more rigorous by approximating the green area by a trapezoid instead of a rectangle, or by using the Mean Value Theorem, but the result is the same. Try the trapezoid.

Do the following Maplet (requires Maple on the computer where this is executed).

Area as an Anti-Derivative: Deriving the Fundamental Theorem of Calculus Rate It

We conclude that \(A_a(x)\), the area function for \(f(x)\), is an antiderivative of \(f(x)\). \[ \dfrac{d}{dx}A_a(x)=f(x) \] This is a differential equation for the area \(A_a(x)\) given the function \(f(x)\) just like \(\dfrac{dx}{dt}=v(t)\) is a differential equation for the position, \(x(t)\), given the velocity, \(v(t)\).

Area as the Solution of an Initial Value Problem

Notice that \(A_a(a)=A(a,a)=0\) since this is the area under \(f(x)\) between \(x=a\) and \(x=a\) which is obviously zero. Consequently, the differential equation together with the initial condition \[ \dfrac{d}{dx}A_a(x)=f(x) \qquad \text{with} \qquad A_a(a)=0 \] is an initial value problem to be solved for \(A_a(x)\). Once we have the solution, \(A_a(x)\), the area under \(f(x)\) above the interval \([a,b]\) is \(A(a,b)=A_a(b)\).

Find the area below \(y=x^2\) above the \(x\)-axis between \(x=1\) and \(x=4\).

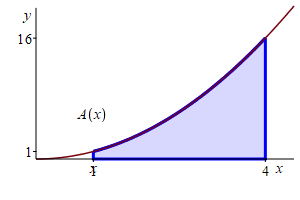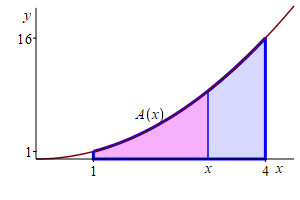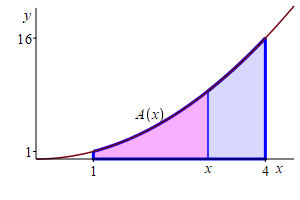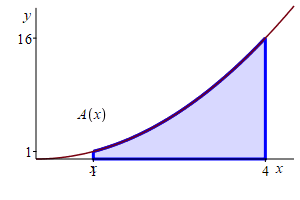
Let \(A(x)\) be the area below \(y=x^2\) above the \(x\)-axis between \(x=1\) and the variable point at \(x\). The answer we need is \(A(4)\).

Notice \(A(x)\) satisfies the initial value problem: \[ \dfrac{d}{dx}A(x)=f(x)=x^2 \qquad \text{with} \qquad A(1)=0 \] An antiderivative of \(f(x)=x^2\) is \(F(x)=\dfrac{x^3}{3}\). So the area function must be \[ A(x)=\dfrac{x^3}{3}+C \] To find the constant, we use the initial condition: \[ A(1)=\dfrac{1^3}{3}+C=0 \qquad \Longrightarrow \qquad C=-\,\dfrac{1}{3} \] So the area function is \[ A(x)=\dfrac{x^3}{3}-\dfrac{1}{3} \] Using this, the area below \(y=x^2\) above the \(x\)-axis between \(x=1\) and \(x=4\) is \[ A(4)=\dfrac{4^3}{3}-\dfrac{1}{3}=21 \]

Find the area below \(y=\sin(x)\) above the interval \([0,\pi]\).

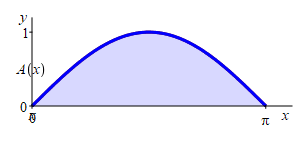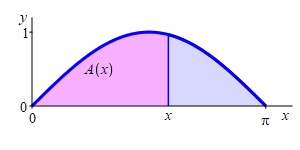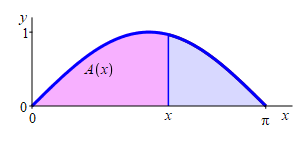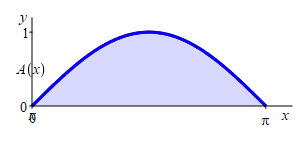
Let \(A(x)\) be the area below \(y=\sin(x)\) above the \(x\)-axis between \(x=0\) and a variable point at \(x\).

The area below \(y=\sin(x)\) above the interval \([0,\pi]\) is \(2\).

Let \(A(x)\) be the area below \(y=\sin(x)\) above the \(x\)-axis between \(x=0\) and a variable point at \(x\). Then \(A(x)\) is the antiderivative of \(\sin(x)\) satisfying \(A(0)=0\). The general antiderivative is \[ A(x)=-\cos(x)+C \] The initial condition says \[ A(0)=-\cos(0)+C=0 \qquad \Longrightarrow \qquad C=\cos(0)=1 \] So \(A(x)=-\cos(x)+1\) and the final answer is \[ A(\pi)=-\cos(\pi)+1=--1+1=2 \]

We check by differentiating the area function \(A(x)=-\cos(x)+1\): \[ A'(x)=\sin(x) \] which is the original curve.

You can also practice computing areas from initial value problems by using the following Maplet (requires Maple on the computer where this is executed):

Area as an Anti-Derivative: Solve an Initial Value Problem Rate It

21. Antiderivatives, Areas and the FTC

e. Area as an Antiderivative

Area as the Solution of an Initial Value Problem

Heading