10. Antiderivatives, Areas and the FTC
Exercises
-
\(f(x)=6x^5\)
\(6x^5\) is the derivative of what?
\(F(x)=x^6+C\)
\(6x^5\) is the derivative of \(x^6\). So: \[ F(x)=x^6+C \]
by
-
\(f(x)=x^{14}\)
\(F(x)=\dfrac{x^{15}}{15}+C\)
We know that the derivative of \(x^{15}\) is \(15x^{14}\). Further, \(f(x)=x^{14}\) is \(\dfrac{1}{15}\) of this value. Therefore the ntiderivative of \(f(x)=x^{14}\) is \(F(x)=\dfrac{x^{15}}{15}+C\)
-
\(\displaystyle f(x)=\dfrac{1}{4}x^4\)
\( \displaystyle F(x)=\dfrac{1}{20}x^5 + C\)
We know that the derivative of \( x^5 \) is \(5x^4\), which is \(20\) times too big, thus we take \( \dfrac{1}{20} \) of it to yield \[ F(x)=\dfrac{1}{20}x^5 +C \] adding a constant to obtain the general form.
cj
We check by differentiating \(F(x)=\dfrac{1}{20}x^5\): \[ F'(x)= \dfrac{1}{20}5x^4= \dfrac{1}{4}x^4 \] which is what we started with.
-
\(g(x)=2x+1 \)
\(G(x)=x^2+x + C\)
We know that the derivative of \( x^2 \) is \(2x\) and the derivative of \(x\) is \(1\), yielding our answer \[ G(x)=x^2+x+C \] adding a constant to obtain the general form.
cj
We check by differentiating \(G(x)=x^2+x\): \[ G'(x)=2x+1 \] which is what we started with.
-
\(p(x)=e^x + \sin 5x \)
\(P(x)=e^x - \dfrac{1}{5}\cos5x + C\)
We know the derivative of \( e^x \) is \( e^x \) and the derivative of \( \cos 5x \) is \( -5\sin 5x \). So the antiderivative of \( e^x \) is \( e^x \) and the antiderivative of \( \sin 5x \) is \( -\,\dfrac{1}{5} \cos 5x \). Thus the complete antiderivative of \(p(x)= e^x + \sin 5x \) is \[ P(x)= e^x - \dfrac{1}{5}\cos5x + C \] adding a constant of integration for the general antiderivative.
cj
We check by differentiating \(P(x)= e^x - \dfrac{1}{5}\cos5x\): \[ P'(x)= e^x-\dfrac{1}{5}(-5\sin 5x) = e^x + \sin 5x \] which is what we started with.
-
\(f(x)=x^3+x^2+2x+8\)
Each term is a derivative by the Power Rule.
\( F(x)=\dfrac{x^4}{4}+\dfrac{x^3}{3}+x^2+8x+C \)
Since \(f(x)=x^3+x^2+2x+8\), then by the Sum, Constant Multiple, and Power Rules, the general antiderivative is: \[\begin{aligned} F(x)&=\dfrac{x^4}{4}+\dfrac{x^3}{3}+2\left(\dfrac{x^2}{2}\right)+8x+C \\ &=\dfrac{x^4}{4}+\dfrac{x^3}{3}+x^2+8x+C \end{aligned}\]
by
We check by differentiating: \[\begin{aligned} F'(x)&=\dfrac{1}{4}\left(4x^3\right)+\dfrac{1}{3}\left(3x^2\right)+2x+8 \\ &=x^3+x^2+2x+8 \end{aligned}\]
-
\(f(x)=\cos x+e^{-3x}\)
The derivative of \(e^{ax}\) is \(ae^{ax}\).
So the antiderivative of \(e^{ax}\) is \(\dfrac{1}{a}e^{ax}\).\(F(x)=\sin(x)-\dfrac{e^{-3x}}{3}+C\)
The derivative of \(e^{-3x}\) is \(-3e^{-3x}\).
So the derivative of \(-\,\dfrac{1}{3}e^{ax}\) is \(e^{-3x}\).
Further, \(\cos x\) is the derivative of \(\sin x\). So \[ F(x)=\sin(x)-\dfrac{e^{-3x}}{3}+C \]by
-
\(h(x)= \cos3x \)
What is the derivative of \(\sin3x\)?
\(H(x)= \dfrac{1}{3}\sin3x + C\)
We know that the antiderivative of \(\cos x\) is \(\sin x\). So we guess \(\sin 3\) for the antiderivative. Deriving, we see that \(\dfrac{d}{dx}\sin 3x=3\cos 3x\), which is three times too large. Thus we conclude the antiderivative of \(h(x)= \cos3x\) is: \[ H(x)=\dfrac{1}{3}\sin3x + C \]
by,cj
We check by differentiating \(H(x)= \dfrac{1}{3}\sin3x\): \[ H'(x)= \dfrac{1}{3}(\cos3x)3=\cos3x \] which is what we started with.
-
\(f(x)=2x\sin(x^2+8)\)
\(F(x)=-\cos (x^2+8)+C\)
We see that \(2x\) is the derivative of \(x^2+8\), which is inside the cosine. The derivative of \(-\cos x\) is \(\sin x\). Therefore we try to apply the Chain Rule and test \(F(x)=-\cos (x^2+8)\). The derivative of this is \(f(x)=2x\sin(x^2+8)\). Therefore, the general antiderivative is \[F(x)=-\cos (x^2+8)+C\]
by
By Chain Rule, the derivative of \(F(x)=-\cos(x^2+8)\) is: \[ F'(x)=-\left[-\sin(x^2+8)\right](2x)=2x\sin(x^2+8) \]
-
\(f(x)=20x^3\)
The derivative of \(x^4\) is \(4x^3\).
\(F(x)=5x^4+C\)
Since the derivative of \(x^4\) is \(4x^3\), the derivative of \(5x^4\) is \(20x^3\). So the antiderivative of \(20x^3\) is \[ 5x^4+C \]
by
-
\(f(x)=80x^{39}\)
\(F(x)=2x^{40}+C\)
The derivative of \(x^{40}\) is \(40x^{39}\). This is half of the value that we desire, so we double \(x^{40}\). The derivative of \(2x^{40}\) is \(80x^{39}\). So the general antiderivative is: \[ F(x)=2x^{40}+C \]
by
-
\(f(x)=(x^2+4)^2\)
First multiply it out.
\(F(x)=\dfrac{x^5}{5}+\dfrac{8}{3}x^3+16x+C\)
Expanding this function we get \(f(x)=x^4+8x^2+16\). Using the derivative Power Rules backwards, the general antiderivative of \(f(x)=x^4+8x^2+16\) is: \[ F(x)=\dfrac{x^5}{5}+\dfrac{8}{3}x^3+16x+C \]
by
Differentiating \(F(x)=\dfrac{x^5}{5}+\dfrac{8}{3}x^3+16x\) gives: \[ F'(x)=x^4+8x^2+16=(x^2+4)^2 \]
-
\(f(x)=3\sqrt x\)
\(F(x)=2x^{3/2}+C\)
Differentiating \(x^{3/2}\) gives \(\dfrac{3}{2}x^{1/2}\) We need twice this amount, so the answer is \(F(x)=2x^{3/2}+C\)
by
Differentiating \(F(x)=2x^{3/2}\) gives \[ F'(x)=2\cdot\dfrac{3}{2}x^{1/2} =3\sqrt x \]
-
\(f(x)=\sec x\tan x\)
Remember the derivatives of the trig functions.
\(F(x)=\sec x+C\)
We know that the derivative of \(\sec x\) is \(\sec x\tan x\). Therefore the general antiderivative of \(\sec x\tan x\) is: \[ F(x)=\sec x+C \]
by
-
\(s(x)= 10x^9+e^{2x}-\sin x+4 \)
\(S(x)= x^{10} + \dfrac{1}{2}e^{2x}+\cos x+4x + C\)
Because the antiderivative of a sum is the sum of the antiderivatives, we take each term of the problem and solve it independently. First, reversing Power Rule says the antiderivative of \(10x^9\) is \( x^{10} \). Second, the antiderivative of \( e^{2x} \) is \( \dfrac{1}{2}e^{2x} \). Third, the antiderivative of \( -\sin x \) is \( \cos x\). And finally, the antiderivative of \( 4 \) is \(4x \). Combining these antiderivatives, we see the general antiderivative of \(s(x)= 10x^9 +e^{2x} - \sin x +4 \) is: \[ S(x)=x^{10} + \dfrac{1}{2}e^{2x}+\cos x+4x + C \]
cj
We check by differentiating \(S(x)= x^{10} + \dfrac{1}{2}e^{2x}+\cos x+4x\): \[ S'(x)= 10x^9 + \dfrac{1}{2}e^{2x}2 - \sin x +4 = 10x^9 +e^{2x} - \sin x +4 \] which is what we started with.
-
\(f(x)=3x^5-2x^3+3x^2+7\)
\( F(x)=\dfrac{x^6}{2}-\dfrac{x^4}{2}+x^3+7x+C \)
Using the Sum, Constant Multiple and Power Rules, the antiderivative of \( f(x)=3x^5-2x^3+3x^2+7 \) is \[ F(x)=\dfrac{x^6}{2}-\dfrac{x^4}{2}+x^3+7x+C \]
by
-
\(b(x) = \dfrac{3}{x} \)
\(B(x) = 3\ln |x| +C \)
We can separate \( \dfrac{3}{x} \) into \( 3 \dfrac{1}{x} \). The antiderivative of \( \dfrac{1}{x} \) equals \( \ln |x| \), yielding: \[ B(x) = 3\ln |x| + C \]
by,cj
We check by differentiating \(B(x) = 3\ln|x|\): \[ B'(x) = 3\left(\dfrac{1}{x}\right) = \dfrac{3}{x} \] which is what we started with.
-
\(d(x)=4^x\)
\(D(x) = \dfrac{4^x}{\ln |4|} + C \)
We use the antiderivative Exponential Rule: If \(f(x)=b^x\) then its antiderivative is \(F(x)=\dfrac{b^x}{\ln |b|} + C \). In this problem \(b=4\). So: \[ D(x) = \dfrac{4^x}{\ln 4} + C \]
cj
We check by differentiating \(D(x) = \dfrac{4^x}{\ln |4|}\): \[ D'(x)= \dfrac{1}{\ln|4|}\ln|4|4^x=4^x \] which is what we started with.
-
\(f(x)=3e^x-\dfrac{4}{x}\)
\( F(x)=3e^{x}-4\ln|x|+C \)
Using the Sum, Constant Multiple, Natural Exponential and Natural Logarithm Rules, the antiderivative of \( f(x)=3e^x-\dfrac{4}{x} \) is \[ F(x)=3e^x-4\ln|x|+C \]
cj
-
\(f(x)=12xe^{2x^2}\)
What is the derivative of \(e^{2x^2}\)? Remember the Chain Rule.
\(F(x)=3e^{2x^2}+C\)
\( \dfrac{d}{dx}2x^2=4x \). This means that by Chain Rule, the derivative of \(e^{2x^2}\) is \(e^{2x^2}4x\). So the antiderivative of \(f(x)\) is: \[ F(x)=3e^{2x^2}+C \]
by
We check by differentiating \(F(x)=3e^{2x^2}\): \[ F'(x)=3e^{2x^2}4x=12xe^{2x^2} \]
-
\(f(x)=3\csc x\cot x\)
\(\csc x\cot x\) is the derivative of what?
\( F(x)=-3\csc x+C \)
\(\csc x\cot x\) is the derivative of \(-\csc x\). Combining this with the Constant Multiple Rule, the antiderivative of \( f(x)=3\csc x\cot x \) is: \[ F(x)=-3\csc x+C \]
by
-
\(q(x)=\dfrac{5}{1+x^2}\)
\(\dfrac{1}{1+x^2}\) is the derivative of what?
\(Q(x) = 5\arctan x +C \)
Recalling that: \[ \dfrac{d}{dx}\arctan x= \dfrac{1}{1+x^2} \] we see that the antiderivative of \( 5 \dfrac{1}{1+x^2} \) is: \[ Q(x)= 5\arctan x +C \]
by,cj
We check by differentiating \(Q(x) = 5\arctan x\): \[ Q'(x)= 5\dfrac{1}{1+x^2} \] which is what we started with.
-
\(f(x)=x^2\sec x\tan x+2x\sec x\)
Think Product Rule. What is the derivative of \(\sec x\)? What is the derivative of \(x^2\)?
\( F(x)=x^2\sec x+C \)
Since \(\dfrac{d}{dx}x^2=2x\) and \(\dfrac{d}{dx}\sec x=\sec x\tan x\), the function is \[ f(x)=x^2\dfrac{d}{dx}\sec x+\sec x\dfrac{d}{dx}x^2 \] The Product Rule gives: \[ F(x)=x^2\sec x+C \]
by
-
\(a(x)=\dfrac{2}{\sqrt{1-x^2}} \)
\(A(x) = 2\arcsin x + C \)
Remembering that: \[ \dfrac{d}{dx}\arcsin x= \dfrac{1}{\sqrt{1-x^2}} \] we see that the antiderivative of \( 2\dfrac{1}{\sqrt{1-x^2}} \) is: \[ A(x)= 2\arcsin x + C \]
cj
We check by differentiating \(A(x) = 2\arcsin x\): \[ A'(x)= 2\dfrac{1}{\sqrt{1-x^2}} \] which is what we started with.
-
\(q(x)=\dfrac{6}{x\sqrt{x^2-1}}\)
What are the derivatives of the inverse trig functions?
\(Q(x)=6\,\mathrm{arcsec}\,x+C\)
Recognizing that: \[ \dfrac{d}{dx}\mathrm{arcsec}\, x= \dfrac{1}{x\sqrt{x^2 - 1}} \] we see that the antiderivative of \( \dfrac{6}{x\sqrt{x^2 - 1}} \) is: \[ Q(x) = 6\,\mathrm{arcsec}\,x + C \]
by,cj
We check by differentiating \(Q(x)= 6\,\mathrm{arcsec}\, x\): \[ Q'(x)= 6\dfrac{1}{x\sqrt{x^2 - 1}} \] which is what we started with.
-
\(f(x)=3\csc^2 x\)
What are the derivatives of the trig functions?
\(F(x)=-3\cot x+C\)
Since \(\csc^2 x\) is the derivative of \(-\cot x\), an antiderivative of \(3\csc^2 x\) is \(-3\cot x\). So the general antiderivative is: \[ F(x)=-3\cot x+C \]
by
Differentiating \(F(x)=-3\cot x\) gives \(F'(x)=-3(-\csc^2 x)=3\csc^2 x\).
-
\(f(x)=\dfrac{1}{7\sqrt{1-x^2}}\)
What are the derivatives of the inverse trig functions?
\(F(x)=\dfrac{\arcsin x}{7}+C\)
The antiderivative of \(\dfrac{1}{\sqrt{1-x^2}}\) is \(\arcsin x\). By the Constant Multiple Rule, our desired antiderivative is: \[ F(x)=\dfrac{\arcsin x}{7}+C \]
by
-
\(z(x) = \dfrac{-8}{1+4x^2} \)
\(Z(x) = -4\arctan 2x + C \)
Recall: \[ \dfrac{d}{du}\arctan u= \dfrac{1}{1+u^2} \] By the Chain Rule for derivatives: \[ \dfrac{d}{dx}\arctan 2x=\dfrac{1}{1+(2x)^2}\,2=\dfrac{2}{1+4x^2} \] So the antiderivative of: \[ z(x) = \dfrac{-8}{1+4x^2}=-4\dfrac{2}{1+4x^2} \] is: \[ Z(x) = -4\arctan 2x + C \]
cj
We check by differentiating \(Z(x) = -4\arctan 2x\). By Chain Rule: \[ Z'(x)= -4\dfrac{1}{1+(2x)^2}2 =\dfrac{-8}{1+4x^2} \] which is what we started with.
-
\(t(x) = \dfrac{6}{x\sqrt{9x^2-1}} \)
\(T(x) = 6\,\mathrm{arcsec}\, 3x + C \)
Recognizing that: \[ \dfrac{d}{du}\mathrm{arcsec}\,u= \dfrac{1}{u\sqrt{u^2 - 1}} \] we see that \[ \dfrac{d}{dx}\mathrm{arcsec}\,3x= \dfrac{1}{3x\sqrt{(3x)^2 - 1}}3 = \dfrac{1}{x\sqrt{9x^2 - 1}} \] by Chain Rule. Thus: \[ T(x) = 6\,\mathrm{arcsec}\, 3x + C \]
cj
We check by differentiating \(T(x) = 6\,\mathrm{arcsec}\, 3x\): \[ T'(x)= 6\dfrac{1}{3x\sqrt{(3x)^2 - 1}}3=\dfrac{6}{x\sqrt{9x^2-1}} \] which is what we started with.
-
\(f(x)=2x\sin (x^2)\)
\(F(x)=-\cos(x^2)+C\)
Notice that the function outside the sine is the derivative of the function inside the sine. We compare this to the Chain Rule: \[ \dfrac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x) \] We see \(f'(u)=\sin u\) and \(g(x)=x^2\). Therefore, the antiderivative of \(f(x)=2x\sin (x^2)\) is: \[ F(x)=-\cos(x^2)+C \]
by
Differentiating \(F(x)=-\cos(x^2)\) gives \(F'(x)=\sin(x^2)\cdot2x=2x\sin(x^2)\).
-
\(f(x)=-3x^2\cos(x^3+7)\)
\(F(x)=-\sin(x^3+7)+C\)
Like the last problem, the derivative of the function inside the cosine is the function outside the cosine. From the Chain Rule, we know that the derivative of \(\sin(x^3+7)\) is \(3x^2\cos(x^2+7)\). We are looking for the negative of the result, so the antiderivative is: \[ F(x)=-\sin(x^3+7)+C \]
by
-
\(f(x)=(x+1)^3\)
\(F(x)=\dfrac{(x+1)^4}{4}+C\)
Here, we notice the derivative of the inside is \(1\). Applying the Chain Rule, we notice that \(\dfrac{d(x+1)^4}{dx}=4(x+1)^3\). So the antiderivative of \(f(x)=(x+1)^3\) is \(F(x)=\dfrac{1}{4}(x+1)^4+C\).
by
-
\(z(x)=\dfrac{1}{x\sqrt{1-x^2}}-\dfrac{1}{x^2}\arcsin x\)
\(Z(x)=\dfrac{\arcsin x}{x}+C\)
Since \(\dfrac{d}{dx}\dfrac{1}{x}=-\dfrac{1}{x^2}\) and \(\dfrac{d}{dx}\arcsin x=\dfrac{1}{\sqrt{1-x^2}}\), this looks like a Product Rule: \[ \dfrac{d}{dx}(P(x)Q(x))=P(x)q(x)+Q(x)p(x) \] We identify: \[\begin{aligned} P(x)=\dfrac{1}{x} \qquad &p(x)=-\,\dfrac{1}{x^2} \\ Q(x)=\arcsin x \qquad &q(x)=\dfrac{1}{\sqrt{1-x^2}} \end{aligned}\] So by the Product Rule in reverse: \[ Z(x)=\dfrac{\arcsin x}{x}+C \]
ad
-
\(r(x)= \dfrac{2xe^x-x^2e^x}{e^{2x}} \)
\(R(x)=\dfrac{x^2}{e^x} +C\)
We solve by pattern matching. Looking at the form of the function, it appears to be a Quotient Rule: \[ \dfrac{d}{dx}\dfrac{P(x)}{Q(x)}=\dfrac{Q(x) p(x)- P(x) q(x)}{Q(x)^2} \] We can identify our two functions. Knowing that the denominator of a Quotient Rule is equal to \( Q(x)^2 \). We see that \( Q(x) = e^x \) and that \( P(x) = x^2 \), giving an antiderivative of \[ R(x)=\dfrac{x^2}{e^x} + C \]
cj
We check by differentiating \(R(x)=\dfrac{x^2}{e^x}\) by Quotient Rule: \[ R'(x)= \dfrac{e^x\dfrac{d}{dx}x^2- x^2\dfrac{d}{dx}e^x}{(e^x)^2} = \dfrac{e^x2x- x^2e^x}{e^{2x}} \] which is what we started with.
-
\(f(x)=e^{2\cos x}\sin x\)
What is the derivative of \(e^{2\cos x}\)?
\(F(x)=-\,\dfrac{1}{2}e^{2\cos x}\)
Since \(-\sin x\) is the derivative of \(\cos x\), we suspect this function is the result of a Chain Rule. Since the derivative of \(e^{2\cos x}\) is \(-2e^{2\cos x}(\sin x)\), we are off by a factor of \(-2\). So the antiderivative of \(f(x)=e^{2\cos x}\sin x\) is \(F(x)=-\,\dfrac{1}{2}e^{2\cos x}\).
We check by differentiating \(F(x)=-\,\dfrac{1}{2}e^{2\cos x}\) using the Chain Rule: \[ F'(x)=-\,\dfrac{1}{2}e^{2\cos x}(-2\sin x) =e^{2\cos x}\sin x=f(x) \] which is what we started with.
-
Derive the logarithmic formulas for:
-
\(\displaystyle \mathrm{arccosh}\,x=\ln\left(x+\sqrt{x^2-1}\right)\)
To say \(\mathrm{arccosh}\) is the inverse of \(\cosh\) means: \(b=\mathrm{arccosh}\,a\) if and only if \(a=\cosh b=\dfrac{e^b+e^{-b}}{2}\) This is the hardest of the three parts of this problem because there are two branches of the \(\cosh\) function. The branches are handled as in the derivation of the formula for \(\mathrm{arcsech}\).
To say \(\mathrm{arccosh}\) is the inverse of \(\cosh\) means: \(b=\mathrm{arccosh}\,a\) if and only if \(a=\cosh b=\dfrac{e^b+e^{-b}}{2}\) Before solving for \(b\), we first note that \(\mathrm{cosh}\,b\) is not \(1-1\) since \(b=u\) and \(b=-u\) give the same value of \(\mathrm{cosh}\,b\). We make the choice to define \(\mathrm{arccosh}\,a\) for the branch of \(\mathrm{cosh}\,b\) with \(b \ge 0\). We now solve the latter equation for \(b\), expecting two solutions from which we want to pick the one with \(b \ge 0\): \[\begin{aligned} 2a&=e^b+e^{-b} \\ 2ae^b&=e^{2b}+1 \\ (e^b)^2-2a&(e^b)+1=0 \end{aligned}\] This is a quadratic equation for \(e^b\). By the quadratic formula: \[ e^b=\dfrac{2a\pm\sqrt{4a^2-4}}{2}=a\pm\sqrt{a^2-1} \] The \(+\) and \(-\) signs give the two solutions and we want the one with \(b \ge 0\). Now if \(b \ge 0\), then \(e^b \ge e^{-b}\). So we need the larger solution which is the one with the \(+\) sign. Then we take the log: \[ b=\ln\left(a+\sqrt{a^2-1}\right)\equiv\mathrm{arccosh}\,a \] So the formula for \(\mathrm{arccosh}\,x\) is: \[ \mathrm{arccosh}\,x=\ln\left(x+\sqrt{x^2-1}\right) \]
-
\(\mathrm{arccoth}\,x=\dfrac{1}{2}\ln\left(\dfrac{x+1}{x-1}\right)\)
To say \(\mathrm{arccoth}\) is the inverse of \(\coth\) means: \(b=\mathrm{arccoth}\,a\) if and only if \(a=\coth b=\dfrac{e^b+e^{-b}}{e^b-e^{-b}}\)
To say \(\mathrm{arccoth}\) is the inverse of \(\coth\) means: \(b=\mathrm{arccoth}\,a\) if and only if \(a=\coth b=\dfrac{e^b+e^{-b}}{e^b-e^{-b}}\) We solve the latter equation for \(b\): \[\begin{aligned} a(e^b-e^{-b})&=e^b+e^{-b} \\ a(e^{2b}-1)&=e^{2b}+1 \\ (a-1)e^{2b}&=a+1 \\ e^{2b}&=\dfrac{a+1}{a-1} \\ b=\dfrac{1}{2}\ln\left(\dfrac{a+1}{a-1}\right)&\equiv\mathrm{arccoth}\,a \end{aligned}\] So the formula for \(\mathrm{arccoth}\,x\) is: \[ \mathrm{arccoth}\,x=\dfrac{1}{2}\ln\left(\dfrac{x+1}{x-1}\right) \]
-
\(\mathrm{arccsch}\,x=\ln\left(\dfrac{1+\sqrt{1+x^2}}{x}\right)\)
To say \(\mathrm{arccsch}\) is the inverse of \(\mathrm{csch}\) means: \(b=\mathrm{arccsch}\,a\) if and only if \(a=\mathrm{csch}\,b=\dfrac{2}{e^b-e^{-b}}\)
To say \(\mathrm{arccsch}\) is the inverse of \(\mathrm{csch}\) means: \(b=\mathrm{arccsch}\,a\) if and only if \(a=\mathrm{csch}\,b=\dfrac{2}{e^b-e^{-b}}\) We solve the latter equation for \(b\): \[\begin{aligned} a(e^b-e^{-b})&=2 \\ a(e^{2b}-1)&=2e^b \\ a(e^b)^2-2(e^b)-a&=0 \\ \end{aligned}\] This is a quadratic equation for \(e^b\). By the quadratic formula: \[ e^b=\dfrac{2\pm\sqrt{4+4a^2}}{2a}=\dfrac{1\pm\sqrt{1+a^2}}{a} \] We pick the \(+\) sign (so that \(e^b\) is positive) and take the log: \[ b=\ln\left(\dfrac{1+\sqrt{1+a^2}}{a}\right)\equiv\mathrm{arccsch}\,a \] So the formula for \(\mathrm{arccsch}\,x\) is: \[ \mathrm{arccsch}\,x=\ln\left(\dfrac{1+\sqrt{1+x^2}}{x}\right) \]
-
-
If a car's velocity at time \(t\) is given by \(v(t)=6t^2+8t+7\), and its position at \(t=0\) is \(x(0)=4\), what is its position at \(t=3\)?
The position is an antiderivative of the velocity.
\(x(3)=115\)
Since position is an antiderivative of velocity, by the Power Rule, the position of the car is given by: \[ x(t)=2t^3+4t^2+7t+C \] To find \(C\), we know that \(x(0)=4\). So: \[ 2(0)^3+4(0)^2+7(0)+C=4 \quad \implies \quad C=4 \] So, the position of the car is: \[ x(t)=2t^3+4t^2+7t+4 \] At \(t=3\) this is \[ x(3)=2(3)^3+4(3)^2+7(3)+4=115 \]
by
-
If a truck's acceleration is \(a(t)=12t^2-10t+12\) and its velocity at time \(t=2\) is \(v(2)=4\), find its velocity at \(t=4\).
The velocity is an antiderivative of acceleration.
\(v(4)=192\)
Since the velocity is an antiderivative of the acceleration, the velocity of the truck is given by: \[ v(t)=4t^3-5t^2+12t+C \] To find \(C\), we use the initial condition \(v(2)=4\) to get: \[ v(2)=4\cdot2^3-5\cdot2^2+12\cdot 2+C=4 \] Solving, this gives \(C=-32\). So the velocity of the truck is \[ v(t)=4t^3-5t^2+12t-32 \] Plugging in \(t=4\) gives \[ v(4)=4\cdot4^3-5\cdot4^2+12\cdot4-32=192 \]
by,cj
-
A rabbit is running with velocity \(v(t)=3t^2+6t+7\). Find the total distance it runs from \(t=1\) to \(t=4\).
The distance it runs is the difference between its initial and final positions.
\(x(4)-x(1)=129\)
Since the position is an antiderivative of the velocity, it is \(x(t)=t^3+3t^2+7t+C\). The positions at \(t=1\) and \(t=4\) are: \[\begin{aligned} x(1)&=1^3+3\cdot1^2+7\cdot1+C=11+C \\ x(4)&=4^3+3\cdot4^2+7\cdot4+C=140+C \end{aligned}\] Subtracting the two positions gives the displacement: \[ x(4)-x(1)=(140+C)-(11+C)=129 \] Notice the constant cancels out.
by
-
A butterfly is taking off from a leaf with an acceleration of \(a(t) =3t^2\,\dfrac{\text{cm}}{\text{sec}^2}\). If the initial position is \( y(0) = 2\,\text{cm} \) and initial velocity is \( v(0) = 0\,\dfrac{\text{cm}}{\text{sec}} \), what is the butterfly's velocity and position at \( t = 4 \) seconds?
\( v(4) = 64\,\dfrac{\text{cm}}{\text{sec}}\)
\( y(4) = \rule{0pt}{12pt}66\,\text{cm}\)First, because the antiderivative of acceleration is velocity, we see that \[ v(t) = t^3 + C \] Because the initial velocity is \( v(0) = 0\), the constant is \( C = 0\) and \(v(t) = t^3\). Evaluating at \( t = 4 \), we see that: \[ v(4)=4^3 = 64\,\dfrac{\text{cm}}{\text{sec}} \] Second, the antiderivative of velocity is position, so we see that: \[ y(t) =\dfrac{1}{4}t^4 + K \] Because \( y(0) = 2\), we find \(K = 2 \) and \(y(t)=\dfrac{1}{4}t^4+2\). Evaluating at \( t = 4 \), we see that: \[ y(4)=\dfrac{1}{4}4^4 + 2 = 66\,\text{cm} \]
Starting with \(y(t)=\dfrac{1}{4}t^4+2\), we compute: \[ y(0)=2 \quad \text{and} \quad y(4)=64+2=66 \] Then \(v(t)=t^3\) and we compute: \[ v(0)=0 \quad \text{and} \quad v(4)=64 \] Finally, \(a(t)=3t^2\).
-
The rate of change of the volume of water in a tank is given by \(R(t)=2t+6\). Find the amount of water in the tank after \(3\) hours if it is initially empty.
The rate of change of the volume of water is the derivative of the volume.
\(V(3)=27\)
The volume of water in the tank is an antiderivative of the rate at which it is being filled. So the volume is: \[ V(t)=t^2+6t+C \] Since the tank is empty at time \(t=0\), the constant is \(C=0\). Therefore the volume is: \[ V(t)=t^2+6t \] Plugging in \(t=3\) gives \(V(3)=3^2+6\cdot3=27\).
-
A car travels so that its accelerates at time \(t\) is \(a(t)=(t+4)\,\dfrac{\text{m}}{\text{sec}^2}\). At time \(t=6\,\text{sec}\), the car's velocity is \(v(6)=40\,\dfrac{\text{m}}{\text{sec}}\) and the car's position is \(x(6)=100\,\text{m}\). Where was the car at time \(t=3\,\text{sec}\)?
\(x(3)=\dfrac{41}{2}\)
Acceleration is the derivative of velocity, so to find velocity we take the antiderivative of acceleration: \[ v(t)=\dfrac{t^2}{2}+4t+C \] To find \(C\), we use the provided initial condition and solve for \(C\): \[ v(6)=18+24+C=40 \qquad \implies \qquad C=-2 \] So \(v(t)\) is: \[ v(t)=\dfrac{t^2}{2}+4t-2 \] Velocity is the derivative of position, so to find position we take the antiderivative of velocity: \[ x(t)=\dfrac{t^3}{6}+2t^2-2t+K \] To find \(K\), we use the provided initial condition and solve for \(K\): \[ x(6)=36+72-12+K=100 \qquad \implies \qquad K=4 \] So \(x(t)\) is: \[ x(t)=\dfrac{t^3}{6}+2t^2-2t+4 \] and \(x(3)\) is: \[ x(3)=\dfrac{3^3}{6}+2\cdot3^2-2\cdot3+4 =\dfrac{41}{2} \]
-
A swimming pool is being filled at a rate of \(R(t)=\dfrac{3}{(2+t)^2}\). Given that the pool is empty at \(t=0\), how much water is in the pool at time \(t=4\)?
\(V(4)=1\)
When we say the rate at which the pool is filled we mean the derivative of the volume. So let \(V(t)\) denote volume. Then \(\dfrac{dV}{dt}=R(t)\) and \(V\) is the antiderivative of \(R(t)\). Then, using the Chain Rule in reverse, \[ V(t)=-\,\dfrac{3}{2+t}+C \] To solve for \(C\), we use the initial condition for \(V\): \[ V(0)=-\,\dfrac{3}{2}+C=0 \qquad \implies \qquad C=\dfrac{3}{2} \] Substituting back, \[ V(t)=\dfrac{3}{2}-\dfrac{3}{2+t} \] and \(V(4)\) is: \[ V(4)=\dfrac{3}{2}-\dfrac{3}{6}=\dfrac{3}{2}-\dfrac{1}{2}=1 \]
ad
-
On the Earth, Moon and Mars, the acceleration of gravity is: \[ g_\text{earth}=9.8\,\dfrac{\text{m}}{\text{sec}^2} \qquad g_\text{moon}=1.6\,\dfrac{\text{m}}{\text{sec}^2} \qquad g_\text{mars}=3.7\,\dfrac{\text{m}}{\text{sec}^2} \] If a ball is dropped from \(10\,\text{m}\), how long will it take to reach the ground:
-
on the Earth?
The velocity is the anti-derivative of the acceleration. The position is the anti-derivative of the velocity.
On Earth, the time is \(t = \sqrt{\dfrac{10}{4.9}}\approx1.43\)
The acceleration is \(a=-g_\text{earth}=-9.8\,\dfrac{\text{m}}{\text{sec}^2}\). So the velocity is \(v=-9.8t+C\). Because the ball is dropped from rest, \(v(0)=0\). So \(C=0\), making the velocity \(v=-9.8t\).
The position is the anti-derivative of the velocity: \(y(t)=-4.9t^2 + K\). Since the ball is dropped at a height of \(y(0)=10\,\text{m}\), we conclude \(K=10\). So the position is \(y(t) = -4.9t^2 + 10 \).
The ball reaches the ground when \(y(t)=0\). We solve for \(t\): \[ -4.9t^2 + 10=0 \implies t^2=\dfrac{10}{4.9} \implies t = \sqrt{\dfrac{10}{4.9}}\approx1.43 \]
bimc
-
on the Moon?
On the Moon, the time is \(t = \sqrt{\dfrac{10}{0.8}}\approx3.54\)
The acceleration is \(a=-g_\text{moon}=-1.6\,\dfrac{\text{m}}{\text{sec}^2}\). So the velocity is \(v=-1.6t+C\). Because the ball is dropped from rest, \(v(0)=0\). So \(C=0\), making the velocity \(v=-1.6t\).
The position is the anti-derivative of the velocity: \(y(t)=-0.8t^2 + K\). Since the ball is dropped at a height of \(y(0)=10\,\text{m}\), we conclude \(K=10\). So the position is \(y(t) = -0.8t^2 + 10 \).
The ball reaches the ground when \(y(t)=0\). We solve for \(t\): \[ -0.8t^2 + 10=0 \implies t^2=\dfrac{10}{0.8} \implies t = \sqrt{\dfrac{10}{0.8}}\approx3.54 \]
bimc
-
on Mars?
On Mars, the time is \(t = \sqrt{\dfrac{10}{1.85}}\approx2.32\)
The acceleration is \(a=-g_\text{mars}=-3.7\,\dfrac{\text{m}}{\text{sec}^2}\). So the velocity is \(v=-3.7t+C\). Because the ball is dropped from rest, \(v(0)=0\). So \(C=0\), making the velocity \(v=-3.7t\).
The position is the anti-derivative of the velocity: \(y(t)=-1.85t^2 + K\). Since the ball is dropped at a height of \(y(0)=10\,\text{m}\), we conclude \(K=10\). So the position is \(y(t) = -1.85t^2 + 10 \).
The ball reaches the ground when \(y(t)=0\). We solve for \(t\): \[ -1.855t^2 + 10=0 \implies t^2=\dfrac{10}{1.85} \implies t = \sqrt{\dfrac{10}{1.85}}\approx2.32 \]
bimc
-
-
The barrel of a cannon makes an angle of \(30^\circ\) above horizontal and the muzzle of the cannon is at \((x,y)=(5\,\text{ft},4\,\text{ft})\). A cannon ball is fired with a muzzle velocity of \(100\,\dfrac{\text{ft}}{\text{sec}}\). Where does it land?
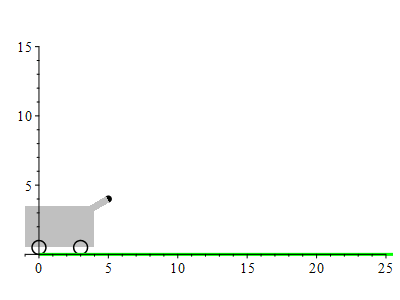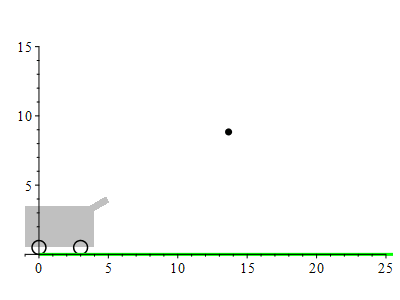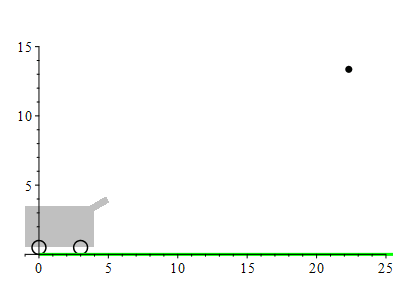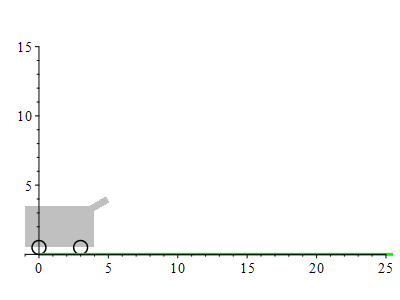
Since gravity pulls downward, the acceleration is \[ \vec a(t)=\langle 0,-g\rangle \] where \(g=32\,\dfrac{\text{ft}}{\text{sec}^2}\).
The cannonball lands at \(x=282\,\text{ft}\).
The position of the cannonball is at \(\vec r(t)=\langle x(t),y(t)\rangle\). The velocity is \(\vec v(t)=\langle x'(t),y'(t)\rangle\). The acceleration is \(\vec a(t)=\langle x''(t),y''(t)\rangle\). Since it feels the gravitation on the surface of the earth, its acceleration is: \[ \vec a(t)=\langle 0,-g\rangle=\langle 0,-32\rangle \] There is a minus sign because the acceleration is downward. The velocity is an antiderivative: \[ \vec v(t)=\langle C_1,-gt+C_2\rangle \] The initial velocity is \(\vec v(0)=\langle 100\cos(30^\circ),100\sin(30^\circ)\rangle\). So \(C_1= 100\cos(30^\circ)\) and \(C_2= 100\sin(30^\circ)\) and so the velocity is: \[ \vec v(t)=\langle 100\cos(30^\circ),-gt+100\sin(30^\circ)\rangle \] The position is an antiderivative: \[ \vec r(t)=\langle 100\cos(30^\circ) t+K_1,-\dfrac{1}{2}gt^2+100\sin(30^\circ) t+K_2\rangle \] The initial position is \(\vec r(0)=\langle 5,4\rangle\). So \(K_1= 5\) and \(K_2= 4\) and so the position is: \[ \vec r(t)=\langle 100\cos(30^\circ) t+5,-\dfrac{1}{2}gt^2+100\sin(30^\circ) t+4\rangle \] The cannonball hits the ground when \(y(t) = 0\). We need to solve: \[ -\dfrac{1}{2}gt^2+100\sin(30^\circ) t+4=0 \] This is a quadreatic equation. So the solutions are given by the quadratic formula: \[\begin{aligned} t&=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a} \\ &=\dfrac{-100\sin(30^\circ)\pm \sqrt{(100\sin(30^\circ))^2-4(-16)(4)}}{2(-16)}\\ &=\dfrac{-(100\dfrac{1}{2})\pm \sqrt{(100\dfrac{1}{2})^2+256}}{-32}\\ &=\dfrac{-50\pm \sqrt{2500+256}}{-32} =\dfrac{25\pm \sqrt{689}}{16} \\ &\approx3.2 \quad\text{or}\quad-0.078\\ \end{aligned}\] We take the positive value so the solution is in the future. So \(t\approx3.2\). Since \(x(t)=100\cos(30^\circ) t\), the cannon ball lands at \[ x(3.2)=100\cos(30^\circ) (3.2)+5=282\,\text{ft} \]

bimc
-
A projectile is launched from the origin with an initial speed of \(v_o\) at an angle of \(\theta_o\) above horizontal.
-
Find the peak height and range as functions of \(v_o\) and \(\theta_o\).
Take the acceleration of gravity to be \(g\) without any units.In the previous problem, we set \(v_o\) to \(100\,\dfrac{\text{ft}}{\text{sec}}\) and \(\theta _0\) to \(30^\circ\), but in this problem we can leave them as their variable forms.
The range is \(x_\text{range}=\dfrac{2v^2_0\cos(\theta_o)\sin(\theta_o)}{g}\) and the peak height is \(y_\text{peak}=\dfrac{v_o^2\sin^2(\theta_o)}{2g}\).
The position of the projectile is \(\vec r(t)=\langle x(t),y(t)\rangle\).
The velocity is \(\vec v(t)=\langle x'(t),y'(t)\rangle\).
The acceleration is \(\vec a(t)=\langle x''(t),y''(t)\rangle\).
Since it feels the gravitation on the surface of the earth, its acceleration is: \[ \vec a(t)=\langle 0,-g\rangle \] There is a minus sign because the acceleration is downward. The velocity is an antiderivative of the acceleration: \[ \vec v(t)=\langle C_1,-gt+C_2\rangle \] The initial velocity is \(\vec v(0)=\langle v_o\cos(\theta_o),v_o\sin(\theta_o )\rangle\). So \(C_1= v_o\cos(\theta_o)\) and \(C_2= v_o\sin(\theta_o)\) and so the velocity is: \[ \vec v(t)=\langle v_o\cos(\theta_o),-gt+v_o\sin(\theta_o)\rangle \] The position is an antiderivative of the velocity: \[ \vec r(t)=\langle v_o\cos(\theta_o)t+K_1, -\dfrac{1}{2}gt^2+v_o\sin(\theta_o)t+K_2\rangle \] The initial position is \(\vec r(0)=\langle 0,0\rangle\). So \(K_1= 0\) and \(K_2= 0\) and so the position is: \[ \vec r(t)=\langle v_o\cos(\theta_o)t, -\dfrac{1}{2}gt^2+v_o\sin(\theta_o)t\rangle \] The projectile hits the ground when \(y(t) = 0\). We solve this by factoring: \[\begin{aligned} -\dfrac{1}{2}gt^2+v_o\sin(\theta_o) t&=0 \\ \left(-\dfrac{1}{2}gt+v_o\sin(\theta_o)\right) t&=0 \\ t=0, t=\dfrac{2v_o\sin(\theta _0)}{g} \end{aligned}\] We started from the ground at \(t=0\). So we use the second solution. We plug this time value back into the \(x\) component of the position to find the range: \[\begin{aligned} x(t)&=v_o\cos(\theta_o) \dfrac{2v_o\sin(\theta _0)}{g}\\ &=\dfrac{2v^2_0\cos(\theta_o)\sin(\theta_o)}{g} \end{aligned}\] The peak height occurs when we stop moving upward and start moving downward. So the \(y\) component of the velocity is \(0\). We solve: \[\begin{aligned} v_y(t) =-gt+v_o\sin(\theta_o)&=0\\ \end{aligned}\] \[ t=\dfrac{v_o\sin(\theta_o)}{g} \] To find the peak height, we plug this \(t\) into the \(y\) component of the position: \[\begin{aligned} y(t)&=-\dfrac{1}{2}gt^2+v_o\sin(\theta_o) t \\ &=-\dfrac{1}{2}g\left(\dfrac{v_o\sin(\theta_o)}{g}\right)^2 +v_o\sin(\theta_o)\left(\dfrac{v_o\sin(\theta_o)}{g}\right) \\ &=\dfrac{v_o^2\sin^2(\theta_o)}{2g} \end{aligned}\] Thus the range is \(x_\text{range}=\dfrac{2v^2_0\cos(\theta_o)\sin(\theta_o)}{g}\) and the peak height is \(y_\text{peak}=\dfrac{v_o^2\sin^2(\theta_o)}{2g}\).bimc
-
Assuming \(v_o\) is held fixed, find the angle, \(\theta_o\), which produces the maximum peak height.
The projectile reaches the maximum peak height when \(\theta_o=90^\circ\).
From the previous part, we know the peak height is \[ y_\text{peak}(\theta_o)=\dfrac{v_0^2\sin^2(\theta_0)}{2g} \] To find the maximum, we set the derivative equal to \(0\) and solve for \(\theta_0\): \[ \dfrac{dy_\text{peak} }{d\theta_o} =\dfrac{2v_0^2\sin(\theta_0)\cos(\theta_0)}{2g}=0 \] \[\begin{aligned} \sin(\theta_0)&\cos(\theta_0)=0\\ \sin(\theta_0)=0 \quad &\text{or} \quad \cos(\theta_0)=0\\ \theta_0&=0^{\circ}, 90^{\circ} \end{aligned}\] We plug \(0^\circ\) and \(90^\circ\), into the peak height to see which returns a greater result: \[\begin{aligned} y_\text{peak}(0)&=\dfrac{v_0^2\sin^2(0^{\circ})}{2g}=0 \\ y_\text{peak}(90)&=\dfrac{v_0^2\sin^2(90^{\circ})}{2g} =\dfrac{v_0^2}{2g} \end{aligned}\] It makes sense that we we reach \(0\) height if we start horizontally, \(\theta_o=0\). So the projectile reaches the maximum peak height when \(\theta_o=90^\circ\) which is straight up.
bimc
-
Assuming \(v_o\) is held fixed, find the angle, \(\theta_o\), which produces the maximum range.
The projectile has the maximum range when \(\theta_o=45^\circ\).
From the first part, we know the range is \[ x_\text{range}(\theta_o)=\dfrac{2v^2_0\cos(\theta_o)\sin(\theta_o)}{g} \] To find the maximum, we set the derivative equal to \(0\) and solve for \(\theta_0\): \[ \dfrac{dx}{d\theta_o} =\dfrac{2v_0^2(-\sin^2(\theta_0)+\cos^2(\theta_0))}{g}=0 \] \[\begin{aligned} -\sin^2(\theta_0)+\cos^2(\theta_0)=0\\ \tan(\theta_0)=1)\\ \theta_0&=45^{\circ} \end{aligned}\] We see that the projectile has the maximum range when \(\theta_o=45^\circ\).
bimc
-
-
\(\dfrac{dy}{dx}=x^3e^x+3e^xx^2\)
\(y=x^3e^x+C\)
This looks like a Product Rule, \[ \dfrac{d(P(x)Q(x))}{dx}=P(x)q(x)+Q(x)p(x) \] with \(P(x)=x^3\) so that \(p(x)=\dfrac{dP}{dx}=3x^2\), and with \(Q(x)=e^x\) so that \(q(x)=\dfrac{dQ}{dx}=e^x\). So by the Product Rule, \[\begin{aligned} y&=P(x)Q(x)+C \\ &=x^3e^x+C \end{aligned}\]
ad
-
\(\dfrac{dp}{dt}=\sin(3t)+\cos(2t)\)
\(p(t)=-\,\dfrac{1}{3}\cos(3t)+\dfrac{1}{2}\sin(2t)+C\).
We separately look at each term: \(\sin(3t)\) and \(\cos(2t)\).
Since \(\dfrac{d}{dx}\cos x=-\sin x\), by the Chain Rule, we know \(\dfrac{d}{dt}\cos(3t)=-3\sin(3t)\). This is off by a factor of \(-3\). So we divide by \(-3\). So the antiderivative of \(\sin(3t)\) is \(-\,\dfrac{1}{3}\cos(3t)\).
Similarly, since \(\dfrac{d}{dx}\sin x=\cos x\), by the Chain Rule, we know \(\dfrac{d}{dt}\sin(2t)=2\cos(2t)\). This is off by a factor of \(2\). So we divide by \(2\). So the antiderivative of \(\cos(2t)\) is \(\dfrac{1}{2}\sin(2t)\).
Putting it all together, we find that: \[ p(t)=-\,\dfrac{1}{3}\cos(3t)+\dfrac{1}{2}\sin(2t)+C \]
ad
-
\(\dfrac{dy}{dx}=x^3e^x+3e^xx^2 \qquad y(2)=8\)
\(y=x^3e^x+8-8e^2\)
In a previous problem, we found that the general antiderivative of \(\dfrac{dy}{dx}=x^3e^x+3e^xx^2\) is \(y=x^3e^x+C\). To determine \(C\) we use the provided initial condition: \[ y(2)=2^3e^2+C=8 \implies C=8-8e^2 \] So the solution is: \[ y=x^3e^x+8-8e^2 \]
-
\(\dfrac{dp}{dt}=\sin(3t)+\cos(2t) \qquad p(0)=\dfrac{2}{3}\)
\(p(t)=-\,\dfrac{1}{3}\cos(3t)+\dfrac{1}{2}\sin(2t)+1\)
In a previous problem, we found that the general antiderivative of \(\dfrac{dp}{dt}=\sin(3t)+\cos(2t)\) is \(p=-\,\dfrac{1}{3}\cos(3t)+\dfrac{1}{2}\sin(2t)+C\). To determine \(C\) we use the provided initial condition: \[\begin{aligned} p(0)&=-\,\dfrac{1}{3}\cos(0)+\dfrac{1}{2}\sin(0)+C=\dfrac{2}{3} \\ C&=\dfrac{2}{3}+\dfrac{1}{3}=1 \end{aligned}\] So the solution is: \[ y=-\,\dfrac{1}{3}\cos(3t)+\dfrac{1}{2}\sin(2t)+1 \]
-
\(\dfrac{dg}{dt}=e^{-2t} \qquad g(0)=4\)
To find \(g\), try differentiating \(e^{-2t}\).
\(g(t)=-\,\dfrac{1}{2}e^{-2t}+\dfrac{9}{2}\)
We need \(g\). We suspect it involves \(e^{-2t}\). So we look at the derivative: \[ \dfrac{d}{dx}[e^{-2t}]=-2e^{-2t} \] If we multiply this by \(-\,\dfrac{1}{2}\), we get \(\dfrac{dg}{dx}\). So the general antiderivative of \(\dfrac{dg}{dx}=e^{-2t}\) is \(g=-\,\dfrac{1}{2}e^{-2t}+C\).
To determine \(C\) we use the provided initial condition: \[ g(0)=-\,\dfrac{1}{2}e^{0}+C=4 \implies C=\dfrac{9}{2} \] So \(g\) is: \[ g=-\,\dfrac{1}{2}e^{-2t}+\dfrac{9}{2} \] -
A rain gage is filling so the rate of change of the volume of water in the gage is \(\dfrac{dV}{dt}=6 e^{-2t}\,\dfrac{\text{cm}^3}{\text{hr}}\). Find the volume in the gauge at time \(t=3\,\text{hr}\) if it starts with \(3\,\text{cm}^3\) at time \(t=0\).
\(V(3)=-3 e^{-6}+6\approx5.993\,\text{cm}^3\)
We start from the rate of change of the volume of water in the gage, \(\dfrac{dV}{dt} =6 e^{-2t}\).
The solution of this differential equation is the antiderivative: \[ V(t)=-3 e^{-2t}+C \] To find \(C\), we use the initial condition for \(V\): \[ V(0)=-3+C=3 \qquad \implies \qquad C=6 \] So the volume is: \[ V(t)=-3 e^{-2t}+6 \] and the volume at \(t=3\,\text{hr}\) is: \[ V(3)=-3 e^{-6}+6\approx5.993\,\text{cm}^3 \]ad
-
Given that the velocity of an object is \(v(t)=2^x\ln(2)\,\dfrac{\text{m}}{\text{sec}}\) and the initial position is \(s(0)=5\,\text{m}\), find the position \(s(t)\) as a function of \(t\).
\(s(t)=2^x+4\)
Since velocity is the derivative of position, we take the antiderivative of velocity to find position: \[ s(t)=2^x+C \] Using the initial condition, \[ s(0)=1+C=5 \qquad \implies \qquad C=4 \] Therefore: \[ s(t)=2^x+4 \]
-
Given the acceleration of an object is \(a(t)=2\sin(2t)\,\dfrac{\text{km}}{\text{sec}^2}\) and \(v(0)=3\,\dfrac{\text{km}}{\text{sec}}\), find \(v(t)\) as a function of \(t\).
\(v(t)=-\cos(2t)+4\)
Since acceleration is the derivative of velocity, we take the antiderivative of acceleration to find velocity: \[ v(t)=-\cos(2t)+C \] Using the initial condition, \[ v(0)=-1+C=3 \qquad \implies \qquad C=4 \] Therefore: \[ v(t)=-\cos(2t)+4 \]
-
Given the acceleration of an object is \(a(t)=\cos(t)\,\dfrac{\text{m}}{\text{sec}^2}\) and the initial position is \(s(0)=7\,\text{m}\) and the initial velocity is \(v(0)=1\,\dfrac{\text{m}}{\text{sec}}\), find the position \(s(t)\) and velocity \(v(t)\) as functions of time \(t\).
\(s(t)=-\cos(t)+t+8\)
\(v(t)=\sin(t)+1\)Since acceleration is the derivative of velocity, we take the antiderivative of acceleration to find velocity: \[ v(t)=\sin(t)+C \] Using the initial condition, \[ v(0)=0+C=1 \quad \implies \quad C=1 \] Therefore: \[ v(t)=\sin(t)+1 \] Since velocity is the derivative of position, we take the antiderivative of velocity to find position: \[ s(t)=-\cos(t)+t+K \] Using the initial condition, \[ s(0)=-1+K=7 \qquad \implies \qquad K=8 \] Therefore: \[ s(t)=-\cos(t)+t+8 \]
-
An object has constant velocity \(v\) and initial position \(s(0)=s_o\). Find the position \(s(t)\) as a function of the time \(t\).
\(s(t)=vt+s_o\)
Since velocity is the derivative of position, we write the position as the general antiderivative of the constant velocity: \[ s(t)=vt+C \] Using the initial condition, \[ s(0)=C=s_o \] we conclude \(C=s_o\). Substituting back, we have: \[ s(t)=vt+s_o \]
-
An object has constant acceleration \(a\) and initial velocity \(v(0)=v_o\). Find the velocity \(v(t)\) as a function of the time \(t\).
\(v(t)=at+v_o\)
Since acceleration is the derivative of velocity, we write the velocity as the general antiderivative of the constant acceleration: \[ v(t)=at+C \] Using the initial condition, \[ v(0)=C=v_o \] we conclude \(C=v_o\). Substituting back, we have: \[ v(t)=at+v_o \]
-
An object has constant acceleration \(a\), initial position \(s(0)=s_o\) and initial velocity \(v(0)=v_o\). Find the position \(s(t)\) and velocity \(v(t)\) as functions of the time \(t\).
\(s(t)=\dfrac{1}{2}at^2+v_ot+s_o\)
\(v(t)=at+v_o\)Since acceleration is the derivative of velocity, we write the velocity as the general antiderivative of the constant acceleration: \[ v(t)=at+C \] Using the initial condition, \[ v(0)=C=v_o \] we conclude \(C=v_o\). Substituting back, we find: \[ v(t)=at+v_o \] Since velocity is the derivative of position, we write the position as the general antiderivative of the velocity: \[ s(t)=\dfrac{1}{2}at^2+v_ot+K \] Using the initial condition, \[ s(0)=K=s_o \] we conclude \(K=s_o\). Substituting back, we find: \[ s(t)=\dfrac{1}{2}at^2+v_ot+s_o \]
-
Find the area below \(y=2x+\cos(x)\) above the interval \(\left[0,\dfrac{\pi}{2}\right]\).
Start by letting \(A(x)\) be the area below \(y=2x+\cos(x)\) above the \(x\)-axis between \(x=0\) and variable point \(x\). Solve an initial value problem for \(A(x)\).
The area below \(y=2x+\cos(x)\) above the interval \(\left[0,\dfrac{\pi}{2}\right]\) is \(A=\dfrac{\pi^2}{4}+1\).
Let \(A(x)\) be the area below \(y=2x+\cos(x)\) above the \(x\)-axis between \(x=0\) and variable point \(x\). Then \(A(x)\) is the antiderivative of \(2x+\cos(x)\) satisfying \(A(0)=0\). The general antiderivative is: \[ A(x)=x^2+\sin(x)+C \] The initial condition says: \[ A(0)=0^2+\sin(0)+C=0\quad \implies\quad C=0 \] So \(A(x)=x^2+\sin(x)\) and the final answer is: \[ A\left(\dfrac{\pi}{2}\right)=\dfrac{\pi^2}{4}+\sin\left(\dfrac{\pi}{2}\right) =\dfrac{\pi^2}{4}+1 \]
ad
We check by differentiating the area function \(A(x)=x^2+\sin(x)\): \[ A'(x)=2x+\cos(x) \] which is the original curve.
-
Find the area below \(y=\dfrac{(x-1)e^x}{x^2}\) above the interval \([2, 4]\).
If you expand the numerator, you will find it is the result of a Quotient Rule.
\(A=\dfrac{e^4}{4}-\dfrac{e^2}{2}\)
Let \(A(x)\) be the area below \(y=f(x)=\dfrac{(x-1)e^x}{x^2}\) above the \(x\)-axis between \(x=3\) and a variable point \(x\). Then \(A(x)\) is the antiderivative of \(y=f(x)\) satisfying \(A(2)=0\). To find the antiderivative, we first expand the numerator: \[ f(x)=\dfrac{xe^x-e^x}{x^2} \] In this form, we see it is the result of a Quotient Rule applied to a qutoent with denominator \(Q(x)=x\) and numerator \(P(x)=e^x\). So the general antiderivative is: \[ A(x)=\dfrac{e^x}{x}+C \] The initial condition says: \[ A(2)=\dfrac{e^2}{2}+C=0 \qquad \implies \qquad C=-\,\dfrac{e^2}{2} \] So \(A(x)=\dfrac{e^x}{x}-\dfrac{e^2}{2}\) and the final area is: \[ A(4)=\dfrac{e^4}{4}-\dfrac{e^2}{2} \]
We check by differentiating the area function \(A(x)=\dfrac{e^x}{x}-\dfrac{e^2}{2}\): \[\begin{aligned} A'(x)&=\dfrac{d}{dx}\left(\dfrac{e^x}{x}\right) \\ &=\dfrac{xe^x-e^x}{x^2} =\dfrac{(x-1)e^x}{x^2} \end{aligned}\] which is the original function.
-
Find the area below \(y=x^{-2}\) above the interval \([3, 6]\).
\(A=\dfrac{1}{6}\)
Let \(A(x)\) be the area below \(y=x^{-2}\) above the \(x\)-axis between \(x=3\) and variable point \(x\). Then \(A(x)\) is the antiderivative of \(y=x^{-2}\) satisfying \(A(3)=0\). Using the Power Rule, the general antiderivative is: \[ A(x)=-x^{-1}+C \] The initial condition says: \[ A(3)=-\,\dfrac{1}{3}+C=0 \qquad \implies C=\dfrac{1}{3} \] So \(A(x)=-x^{-1}+\dfrac{1}{3}\) and the final answer is: \[ A(6)=-\,\dfrac{1}{6}+\dfrac{1}{3}=\dfrac{1}{6} \]
ad
For each function, find the area below it above the specified interval.
-
Find the area below \(f(x)=x\sin(x^2)\) above the interval \([0, \sqrt{\pi}]\).
To find the antiderivative, try differentiating \(\cos(x^2)\).
\(A(0, \sqrt{\pi})=1\)
We need the antiderivative of \(f(x)=x\sin(x^2)\). We suspect it will involve \(\cos(x^2)\). So we look at the derivative \[ \dfrac{d}{dx}[\cos(x^2)]=-\sin(x^2)2x \] If we multiply this by \(-\,\dfrac{1}{2}\), we get \(f\). So an antiderivative of \(f(x)=x\sin(x^2)\) is \(F(x)=-\,\dfrac{1}{2}\cos(x^2)\). Then, the area is: \[\begin{aligned} A\left(0, \sqrt{\pi}\right)&=\left[-\,\dfrac{1}{2}\cos(x^2)\right]_{0}^{\sqrt{\pi}} \\ &=-\,\dfrac{1}{2}\cos(\pi)+\dfrac{1}{2}\cos(0) \\ &=\dfrac{1}{2}+\dfrac{1}{2}=1 \end{aligned}\]
ad
We check by differentiating \(F(x)=-\,\dfrac{1}{2}\cos(x^2)\): \[\begin{aligned} F'(x)&=\dfrac{d}{dx}\left[-\,\dfrac{1}{2}\cos(x^2)\right] \\ &=-\,\dfrac{1}{2}\left[-\sin(x^2)2x\right] \\ &=x\sin(x^2) \end{aligned}\] which is the original function \(f(x)\).
-
Find the area below \(f(x)=\dfrac{2}{x}\) above the interval \([2,4]\).
\(A(2,4)=2\ln(2)\approx1.386\)
An antiderivative of \(f(x)=\dfrac{2}{x}\) is \(F(x)=2\ln(x)\). So the area is: \[\begin{aligned} A\left(2, 4\right)&=\left[\rule{0pt}{10pt}2\ln(x)\right]_{2}^{4} \\ &=2\ln(4)-2\ln(2) \\ &=4\ln(2)-2\ln(2) \\ &=2\ln(2)\approx1.386 \end{aligned}\] In the next-to-last step, we used \(\ln4=\ln2^2=2\ln2\).
We check by differentiating \(F(x)=2\ln(x)\): \[\begin{aligned} F'(x)&=\dfrac{d}{dx}\left(2\ln(x)\right) \\ &=2\dfrac{d}{dx}(\ln(x)) =\dfrac{2}{x} \end{aligned}\] which is the original function \(f(x)\).
ad
-
Find the area below \(f(x)=e^x\) above the interval \([0,3]\).
\(A(0,3)=e^3-1\)
An antiderivative of \(e^x\) is \(e^x\). So the area is: \[\begin{aligned} A(0,3)&=\left[\rule{0pt}{10pt}e^x\right]_0^3 \\ &=e^3-1 \end{aligned}\]
ad
-
\(\displaystyle f(x)=e^{3x+1}\)
\(\displaystyle F(x)=\dfrac{1}{3}e^{3x+1}+C\)
We know that the derivative of \(e^{3x+1}\) is \(3e^{3x+1}\). This is \(3\) times too much. So the antiderivative of \(\displaystyle f(x)=e^{3x+1}\) is: \[ F(x)=\dfrac{1}{3}e^{3x+1}+C \]
ad
-
\(\displaystyle g(x)=\csc^2 x\)
\(\displaystyle G(x)=-\cot x+C\)
We know that the derivative of \(\cot(x)\) is \(-\csc^2 x\). This is exactly \(-g(x)\). So the antiderivative of \(\displaystyle g(x)=\csc^2 x\) is: \[ G(x)=-\cot x+C \]
ad
-
\(\displaystyle h(x)=e^x+x^e\)
\(H(x)=e^x+\dfrac{x^{e+1}}{e+1}+C\)
We use the Sum Rule to find that \(H(x)\) is the antiderivative of \(e^x\) plus the antiderivative of \(x^e\). The antiderivative of \(e^x\) is just \(e^x\), and using the Power Rule with the exponent of \(e\), we find that the antiderivative of \(x^e\) is \(\dfrac{x^{e+1}}{e+1}\). So the antiderivative of \(h(x)=e^x+x^e\) is: \[ H(x)=e^x+\dfrac{x^{e+1}}{e+1}+C \]
ad
-
\(w(x)=\dfrac{2x\sin(x)-x^2\cos(x)}{\sin^2(x)}\)
\(W(x)=\dfrac{x^2}{\sin(x)}+C\)
The function looks like a Quotient Rule: \[ \dfrac{d}{dx}\left(\dfrac{P(x)}{Q(x)}\right)=\dfrac{Q(x)p(x)-P(x)q(x)}{Q^2(x)} \] The denominator of \(w(x)\) is \(\sin^2(x)\). So \(Q(x)\) must be \(\sin(x)\). Since \(\dfrac{d}{dx}\sin(x)=\cos(x)\) and \(\dfrac{d}{dx}x^2=2x\), we identify: \[\begin{aligned} P(x)=x^2 \qquad &p(x)=2x \\ Q(x)=\sin x \qquad &q(x)=\cos x \end{aligned}\] So the antiderivative of \(w(x)\) is: \[ W(x)=\dfrac{x^2}{\sin(x)}+C \]
ad
-
\(z(x)=\dfrac{\arcsin x}{1+x^2}+\dfrac{\arctan x}{\sqrt{1-x^2}}\)
\(Z(x)=\arcsin x \arctan x+C\)
This looks like a Product Rule: \[ \dfrac{d}{dx}(P(x)Q(x))=P(x)q(x)+Q(x)p(x) \] Since \(\dfrac{d}{dx}\arcsin x=\dfrac{1}{\sqrt{1-x^2}}\) and \(\dfrac{d}{dx}\arctan x=\dfrac{1}{1+x^2}\), we identify: \[\begin{aligned} P(x)=\arcsin x \qquad &p(x)=\dfrac{1}{\sqrt{1-x^2}} \\ Q(x)=\arctan x \qquad &q(x)=\dfrac{1}{1+x^2} \end{aligned}\] So by the Product Rule in reverse: \[ Z(x)=\arcsin x \arctan x+C \]
ad
-
\(y(x)=\sin(x)\sinh(x)+\cosh(x)\cos(x)\)
Think Product Rule. What are the derivatives of \(\sin(x)\), \(\cos(x)\), \(\sinh(x)\) and \(\cosh(x)\)?
\(Y(x)=\sin(x)\cosh(x)+C\)
This looks like a Product Rule: \[ \dfrac{d}{dx}(P(x)Q(x))=P(x)q(x)+Q(x)p(x) \] Since \(\dfrac{d}{dx}\sin x=\cos x\) and \(\dfrac{d}{dx}\cosh x=\sinh x\), we identify: \[\begin{aligned} P(x)=\sin(x) \qquad &p(x)=\cos(x) \\ Q(x)=\cosh(x) \qquad &q(x)=\sinh(x) \end{aligned}\] So by the Product Rule: \[ Y(x)=\sin(x)\cosh(x)+C \] (Note: If we had taken \(Q(x)=\sinh(x)\) and \(P(x)=\cos(x)\) then the sign between the terms would have been wrong.)
ad
-
Find the area below \(y=x+x^2+x^3+x^4\) above the interval \([0,1]\).
The area below \(y=x+x^2+x^3+x^4\) above the interval \([0,1]\) is \(A=\dfrac{77}{60}\).
Let \(A(x)\) be the area below \(y=x+x^2+x^3+x^4\) above the \(x\)-axis between \(x=0\) and a variable point \(x\). Then \(A(x)\) is the antiderivative of \(f(x)=x+x^2+x^3+x^4\) satisfying \(A(0)=0\). The general antiderivative is: \[ A(x)=\dfrac{x^2}{2}+\dfrac{x^3}{3}+\dfrac{x^4}{4}+\dfrac{x^5}{5}+C \] The initial condition says: \[ A(0)=C=0\quad\implies\quad C=0 \] So \(A(x)=\dfrac{x^2}{2}+\dfrac{x^3}{3}+\dfrac{x^4}{4}+\dfrac{x^5}{5}\) and the final answer is: \[\begin{aligned} A(1)&=\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5} \\ &=\dfrac{30}{60}+\dfrac{20}{60}+\dfrac{15}{60}+\dfrac{12}{60} =\dfrac{77}{60} \end{aligned}\]
ad
We check by differentiating the area function \(A(x)=\dfrac{x^2}{2}+\dfrac{x^3}{3}+\dfrac{x^4}{4}+\dfrac{x^5}{5}\): \[ A'(x)=x+x^2+x^3+x^4 \] which is the original curve.
-
Starting from the origin, a ball is thrown at the initial angle of \(\theta=\dfrac{\pi}{6}\,\text{rad}\) from the ground with a speed of \(15\,\dfrac{\text{m}}{\text{sec}}\). Assuming that the acceleration due to gravity is \(10\,\dfrac{\text{m}}{\text{sec}^2}\) downward, what is the ball's position \(1\,\text{sec}\) after it is thrown?
\( x(1)=\dfrac{15\sqrt{3}}{2}\,\text{m} \quad \text{and} \quad y(1)=\dfrac{5}{2}\,\text{m} \)
Let \(x(t)\) and \(y(t)\) be the ball's position at time \(t\). The ball starts at the origin, \((x(0),y(0))=(0,0)\). Let \(\vec v=\langle v_x(t), v_y(t)\rangle\) be the ball's velocity at time \(t\). So the ball's initial velocity is \[ v_x(0)=15\cos\dfrac{\pi}{6}=\dfrac{15\sqrt{3}}{2} \quad \text{and} \quad v_y(0)=15\sin\dfrac{\pi}{6}=\dfrac{15}{2} \] Let \(\vec a=\langle a_x(t),a_y(t)\rangle\) be the ball's acceleration at time \(t\) which is given as \[ a_x(t)=0 \quad \text{and} \quad a_y(t)=-10 \] Since the velocity is an antiderivative of the acceleration, \[ v_x(t)=C_1 \quad \text{and} \quad v_y(t)=-10t+C_2 \] To find the constants \(C_1\) and \(C_2\), we use the initial conditions: \[ v_x(0)=C_1=\dfrac{15\sqrt{3}}{2} \quad \text{and} \quad v_y(0)=C_2=\dfrac{15}{2} \] So velocity is: \[ v_x(t)=\dfrac{15\sqrt{3}}{2} \quad \text{and} \quad v_y(t)=-10t+\dfrac{15}{2} \] Since the position is an antiderivative of velocity, \[ x(t)=\dfrac{15\sqrt{3}}{2}t+K_1 \quad \text{and} \quad y(t)=-5t^2+\dfrac{15}{2}t+K_2 \] To find the constants \(K_1\) and \(K_2\), we use the initial conditions: \[ x(0)=K_1=0 \quad \text{and} \quad y(0)=K_2=0 \] So the position is: \[ x(t)=\dfrac{15\sqrt{3}}{2}t \quad \text{and} \quad y(t)=-5t^2+\dfrac{15}{2}t \] and the position at \(t=1\) is: \[ x(1)=\dfrac{15\sqrt{3}}{2}\,\text{m} \quad \text{and} \quad y(1)=-5+\dfrac{15}{2}=\dfrac{5}{2}\,\text{m} \]
-
Find the general solution to the differential equation: \(\dfrac{dp}{dt}=3t+t\cos\left(\dfrac{t^2}{2}\right)\).
\(p(t)=\dfrac{3}{2}t^2+\sin\left(\dfrac{t^2}{2}\right)+C\)
We look at each term seperately. First, the antiderivative of \(3t\) is \(\dfrac{3}{2}t^2\) by the Power Rule, and, using the Chain Rule, the antiderivative of \(t\cos\left(\dfrac{t^2}{2}\right)\) is \(\sin\left(\dfrac{t^2}{2}\right)\). Putting it all together, we find that: \[ p(t)=\dfrac{3}{2}t^2+\sin\left(\dfrac{t^2}{2}\right)+C \]
ad
-
Find the solution to the initial value problem: \(\dfrac{dp}{dt}=3t+t\cos\left(\dfrac{t^2}{2}\right)\) with \(p(\sqrt{\pi})=2\).
\(p=\dfrac{3}{2}t^2+\sin\left(\dfrac{t^2}{2}\right)+1-\dfrac{3}{2}\pi\)
In the previous problem, we found that the general antiderivative of \(\dfrac{dp}{dt}=3t+t\cos\left(\dfrac{t^2}{2}\right)\) is \(p=\dfrac{3}{2}t^2+\sin\left(\dfrac{t^2}{2}\right)+C\). To determine \(C\) we use the provided initial condition: \[\begin{aligned} p(\sqrt{\pi})&=\dfrac{3}{2}\pi+\sin\left(\dfrac{\pi}{2}\right)+C=2 \\ \dfrac{3}{2}\pi+1+C&=2 \quad \implies \quad C=1-\dfrac{3}{2}\pi \end{aligned}\] So the solution is: \[ p=\dfrac{3}{2}t^2+\sin\left(\dfrac{t^2}{2}\right)+1-\dfrac{3}{2}\pi \]
-
Given the acceleration of an object is \(a(t)=\sec^2(t)\,\dfrac{\text{km}}{\text{sec}^2}\) and \(v(0)=3\,\dfrac{\text{km}}{\text{sec}}\) find \(v(t)\) as a function of \(t\).
\(v(t)=\tan(t)+3\)
Since acceleration is the derivative of velocity, we take the antiderivative of acceleration to find velocity: \[ v(t)=\tan(t)+C \] Using the initial condition, \[ v(0)=0+C=3 \qquad \implies \qquad C=3 \] Therefore: \[ v(t)=\tan(t)+3 \]
-
Find the area below \(f(x)=x^3+2^x\ln(2)\) above the interval \([0,2]\).
\(A(0,2)=7\)
An antiderivative of \(f(x)=x^3+2^x\ln(2)\) is \(F(x)=\dfrac{x^4}{4}+2^x\). So the area is: \[\begin{aligned} A\left(0,2\right)&=\left[\dfrac{x^4}{4}+2^x\right]_{0}^{2} \\ &=\dfrac{2^4}{4}+2^2-\dfrac{0^4}{4}-2^0 \\ &=4+4-1=7 \end{aligned}\]
For each function, find its general antiderivative.
For each function, find its general antiderivative.
Find the general solution of each differential equation.
Find the solution of each initial value problem.
In the following problems, find the area by solving an initial value problem.
Review Exercises
Find the general antiderivatives.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum