8. Related Rates

Exercises

a. For Variables Related by an Equation

1

1. If \(x\) and \(y\) are related by \(x^2y+xy^3=12\) and currently \(x=3\), \(y=1\) and \(\dfrac{dx}{dt}=3\), find \(\dfrac{dy}{dt}\).

   Differentiate using the Chain Rule and Product Rule.

   \(\dfrac{dy}{dt}=-\,\dfrac{7}{6}\)

   We differentiate using the Chain Rule and Product Rule: \[ \dfrac{d}{dt}\left[x^2y+xy^3\right]= \dfrac{d}{dt}\left[12\right] \] \[ 2xy\dfrac{dx}{dt}+x^2\dfrac{dy}{dt}+ y^3\dfrac{dx}{dt}+3xy^2\dfrac{dy}{dt} =0 \] We plug in \(x=3\), \(y=1\) and \(\dfrac{dx}{dt}=3\): \[ 2(3)(1)(3)+(3)^2\dfrac{dy}{dt}+(1)^3(3)+3(3)(1)^2 \dfrac{dy}{dt}=0 \] \[ 18+9\dfrac{dy}{dt}+3+9\dfrac{dy}{dt} =0 \] and solve for \(\dfrac{dy}{dt}\): \[ 18\dfrac{dy}{dt}=-21 \] \[ \dfrac{dy}{dt}=-\,\dfrac{7}{6} \]

   tj 

2. Two variables, \(a\) and \(b\), are related by the equation \(a^3b+2ab^3=3\). When \(a=1\), \(b=1\) and \(\dfrac{da}{dt}=2\), what is \(\dfrac{db}{dt}\)?

   Differentiate using the Chain Rule and the Product Rule.

   \(\dfrac{db}{dt}=-\,\dfrac{10}{7}\)

   We differentiate using the Chain Rule and the Product Rule: \[ 3a^2b\dfrac{da}{dt}+a^3\dfrac{db}{dt}+2b^3\dfrac{da}{dt}+6ab^2\dfrac{db}{ dt}=0 \] We plug in numbers and solve: \[ 3\left(1\right)^2\left(1\right)2+\left(1\right)^3\dfrac{db}{dt}+2\left( 1\right)^3 2+6\left(1\right)\left(1\right)^2\dfrac{db}{dt}=0 \] \[ 10+7\dfrac{db}{dt}=0 \] \[ \dfrac{db}{dt}=-\,\dfrac{10}{7} \]

   tj 

3. The variables \(x\) and \(y\) are related by \(4xy^4+x^4y=24\). When \(x=2\) and \(y=1\), what is \(\dfrac{dy}{dt}\), assuming \(\dfrac{dx}{dt}=-3\)?

   \(\dfrac{dy}{dt}=\dfrac{9}{4}\)

   We differentiate using the Chain Rule and the Product Rule: \[ 4y^4\dfrac{dx}{dt}+16xy^3\dfrac{dy}{dt}+4x^3y\dfrac{dx}{dt}+x^4\dfrac{dy}{dt} =0 \] We plug in numbers and solve: \[ 4(1)^4(-3)+16(2)(1)^3\dfrac{dy}{dt}+4(2)^3(1)(-3)+(2)^4\dfrac{dy}{dt} =0 \] \[ -108+48\dfrac{dy}{dt}=0 \] \[ \dfrac{dy}{dt} =\dfrac{108}{48} =\dfrac{9}{4} \]

   tj 

4. If \(\alpha\) and \(\beta\) are related by \(\alpha\cos\beta+\beta\sin\alpha=\dfrac{\pi}{4}\), find \(\dfrac{d\beta}{dt}\) when \(\alpha=\dfrac{\pi}{6}\), \(\beta=\dfrac{\pi}{3}\) and \(\dfrac{d\alpha}{dt}=\dfrac{\pi}{12}\).

   \( \dfrac{d\beta}{dt}= \dfrac{3\pi+\pi^2\sqrt{3}}{6\pi\sqrt{3}-36} \)

   We differentiate using the Chain Rule and the Product Rule: \[ \cos\beta \dfrac{d\alpha}{dt}- \alpha\sin\beta \dfrac{d\beta}{dt}+ \sin\alpha \dfrac{d\beta}{dt}+ \beta\cos\alpha \dfrac{d\alpha}{dt}=0 \] We plug in numbers and solve: \[ \dfrac{\pi}{12}\cos\dfrac{\pi}{3}- \dfrac{\pi}{6}\sin\dfrac{\pi}{3} \dfrac{d\beta}{dt}+ \sin\dfrac{\pi}{6} \dfrac{d\beta}{dt}+ \dfrac{\pi}{3}\dfrac{\pi}{12}\cos\dfrac{\pi}{6}=0 \] \[ \dfrac{\pi}{24}- \dfrac{\pi\sqrt{3}}{12} \dfrac{d\beta}{dt}+ \dfrac{1}{2} \dfrac{d\beta}{dt}+ \dfrac{\pi^2\sqrt{3}}{72}=0 \] \[ \dfrac{3\pi+\pi^2\sqrt{3}}{72}- \dfrac{\pi\sqrt{3}-6}{12} \dfrac{d\beta}{dt}=0 \] \[ \dfrac{\pi\sqrt{3}-6}{12} \dfrac{d\beta}{dt}= \dfrac{3\pi+\pi^2\sqrt{3}}{72} \] \[ \dfrac{d\beta}{dt}= \dfrac{3\pi+\pi^2\sqrt{3}}{6\pi\sqrt{3}-36} \]

   tj 

5. The curve at the right is an example of an astroid. Its equation is \(x^{2/3}+y^{2/3}=5\). A dot is moving around the astroid. When the dot is at the point \((1,8)\), it satisfies \(\dfrac{dx}{dt}=-2\). Find \(\dfrac{dy}{dt}\) at that point.

   

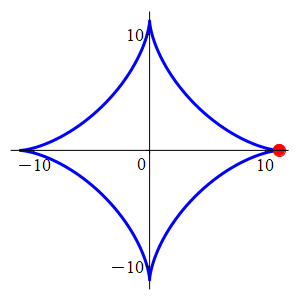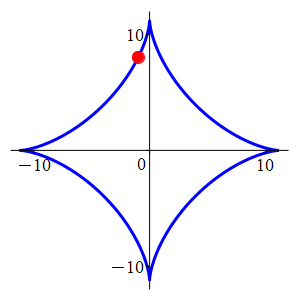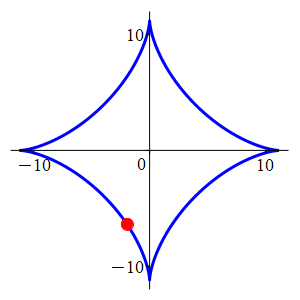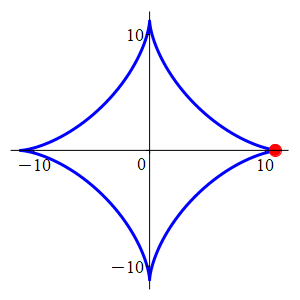
   Implicitly differentiate the equation.

   \(\dfrac{dy}{dt}=4\)

   We differentiate the equation using the Chain and Power Rules and simplify: \[\begin{aligned} \dfrac{2}{3}x^{-1/3}\dfrac{dx}{dt}+\dfrac{2}{3}y^{-1/3}\dfrac{dy}{dt}&=0 \\ x^{-1/3}\dfrac{dx}{dt}+y^{-1/3}\dfrac{dy}{dt}&=0 \end{aligned}\] We plug in \(x=1\), \(y=8\) and \(\dfrac{dx}{dt}=-2\) and solve: \[\begin{aligned} -2+\dfrac{1}{2}\dfrac{dy}{dt}&=0 \\ \dfrac{dy}{dt}&=4 \end{aligned}\]

6. The equation \(\dfrac{j+k^2}{j^2+k}=-1\) relates the variables \(j\) and \(k\). When \(j=-0.6\) and \(k=0.2\), what is \(\dfrac{dk}{dt}\), assuming \(\dfrac{dj}{dt}=2\)?

   First simplify by multiplying both sides by the denominator.

   \(\dfrac{dk}{dt}=\dfrac{2}{7}\)

   We first rewrite the equation as: \[ j+k^2=-j^2-k \] We differentiate using the Chain Rule and the Power Rule: \[ \dfrac{dj}{dt}+2k\dfrac{dk}{dt}=-2j\dfrac{dj}{dt}-\dfrac{dk}{dt} \] We plug in and solve: \[ 2+2(0.2)\dfrac{dk}{dt}=-2(-0.6)(2)-\dfrac{dk}{dt} \] \[ 1.4\dfrac{dk}{dt}=0.4 \] \[ \dfrac{dk}{dt}=\dfrac{2}{7} \]

   tj 

7. If \(h=\dfrac{\pi}{4}\), \(k=\dfrac{\pi}{4}\), and \(\dfrac{dk}{dt}=2\), what is \(\dfrac{dh}{dt}\), assuming \(h\) and \(k\) are related by \(h\sin(k)-k\cos(h)=0\)?

   \(\dfrac{dh}{dt}=\dfrac{8-2\pi}{4+\pi}\)

   We differentiate using the Chain Rule: \[\begin{aligned} \sin(k)\dfrac{dh}{dt}+h\cos(k)\dfrac{dk}{dt}-\cos(h)\dfrac{ dk}{dt}+k\sin(h)\dfrac{dh}{dt}&=0 \\ \left[\rule{0pt}{10pt}\sin(k)+k\sin(h)\right]\dfrac{dh}{dt} +\left[\rule{0pt}{10pt}h\cos(k)-\cos(h)\right]\dfrac{dk}{dt}&=0 \end{aligned}\] We plug in numbers and solve: \[\begin{aligned} \left(\dfrac{1}{\sqrt{2}}+\dfrac{\pi}{4}\dfrac{1}{\sqrt{2}}\right)\dfrac{dh}{dt} +2\left( \dfrac{\pi}{4}\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{2}}\right)&=0 \\ \left(1+\dfrac{\pi}{4}\right)\dfrac{dh}{dt} +\left(\dfrac{\pi}{2}-2\right)&=0 \end{aligned}\] \[ \dfrac{dh}{dt}=\dfrac{2-\dfrac{\pi}{2}}{1+\dfrac{\rule{0pt}{6pt}\pi}{4}} =\dfrac{8-2\pi}{4+\pi} \]

   tj 

b. Word Problems

1

8. A girl is blowing up a spherical balloon. Currently the radius is \(r=6\,\text{cm}\). If the volume is increasing at \(4\,\dfrac{\text{cm}^3}{\text{sec}}\). How fast is the radius increasing?

   

   You need to find \(\dfrac{dr}{dt}\).
   What is the formula for the volume of a sphere?

   \(\dfrac{dr}{dt}=\dfrac{1}{36\pi}\dfrac{\text{cm}}{\text{sec}}\)

   The volume of a sphere is \(V=\dfrac{4}{3}\pi r^3\). We apply \(\dfrac{d}{dt}\) to both sides: \[ \dfrac{dV}{dt}=4\pi r^2\dfrac{dr}{dt} \] We solve for \(\dfrac{dr}{dt}\) and plug in numbers: \[\begin{aligned} \dfrac{dr}{dt}&=\dfrac{1}{4\pi r^2}\dfrac{dV}{dt} \\ &=\dfrac{1}{4\pi (6)^2}(4) =\dfrac{1}{36\pi}\dfrac{\text{cm}}{\text{sec}} \end{aligned}\]

   tj 

9. A sponge cube is absorbing water and expanding. Currently, it has side length \(s=5\,\text{in}\). The side length is increasing at a rate of \(0.1\dfrac{\text{in}}{\text{sec}}\). At what rate is the volume increasing?

   

   What is the volume of a cube?

   \(\dfrac{dV}{dt} = 7.5\dfrac{\text{in}^3}{\text{sec}}\)

   The volume of a cube is \(V=s^3\). We differentiate both sides and plug in numbers: \[ \dfrac{dV}{dt} = 3s^2\dfrac{ds}{dt} =3(5)^2(0.1)=7.5\dfrac{\text{in}^3}{\text{sec}} \]

   tj 

10. A \(5\,\text{ft}\) tall woman is walking away from a \(15\,\text{ft}\) tall light pole at a speed of \(2\,\dfrac{\text{ft}}{\text{sec}}\). How fast is the tip of her shadow moving when she is \(20\,\text{ft}\) away from the pole?

    

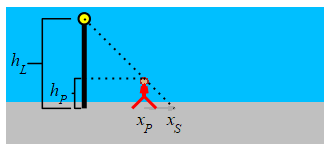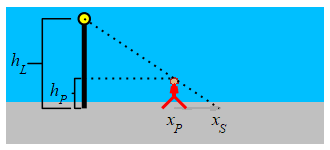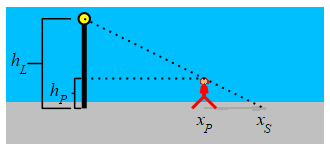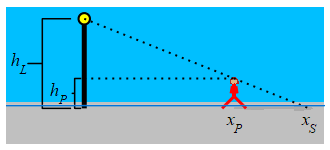
    Use similar triangles.

    \(\displaystyle \dfrac{d x_{S}}{dt}=3\dfrac{\text{ft}}{\text{sec}}\)

    The height of the woman is \(h_P=5\) and the height of the light pole is \(h_L=15\). The position of the woman is \(x_P\) and the tip of the shadow is at \(x_S\). Note: \(h_P\) and \(h_L\) are constants but \(x_P\) and \(x_S\) are variables.

    We look at two similar triangles: The first has corners at the top of the pole, the point on the pole at the same height as the person's head, and the top of the person's head. The second has corners at the top of the pole, the bottom of the pole, and the tip of the person's shadow. Therefore, \(\dfrac{x_S}{h_L}=\dfrac{x_P}{h_L-h_P}\). This means that: \[ x_{S}=\dfrac{h_{L}}{h_{L}-h_{P}}x_{P}=\dfrac{15}{15-5}x_{P}=1.5x_{P} \] We differentiate and plug in the woman's speed: \[ \dfrac{d x_{S}}{dt}=1.5\dfrac{d x_{P}}{dt} =1.5\cdot2\,\dfrac{\text{ft}}{\text{sec}} =3\,\dfrac{\text{ft}}{\text{sec}} \]

    tj 

11. Water is being poured into a cylindrical tank at a rate of \(2\pi\,\dfrac{\text{m}^3}{\text{min}}\). If the tank has a radius of \(4\,\text{m}\), how fast is the height going up?

    

    What is the formula for the volume of a cylinder?

    \( \dfrac{dh}{dt}=\dfrac{1}{8}\,\dfrac{\text{m}}{\text{min}} \)

    The volume of a cylinder is \(V=\pi r^2 h\). Since the radius is \(4\), the volume becomes: \[ V=16\pi h \] We solve for \(h\) and differentiate: \[ h=\dfrac{1}{16\pi}V \] \[ \dfrac{dh}{dt}=\dfrac{1}{16\pi}\dfrac{dV}{dt} =\dfrac{1}{16\pi}2\pi =\dfrac{1}{8}\dfrac{\text{m}}{\text{min}} \]

    tj 

12. A \( 5 \,\text{m}\) long ladder is sliding down a wall. The top of the ladder is at a height \(a\,\text{m}\) on the wall and the base is a distance \(b\,\text{m}\) from the wall. If it is sliding down at the rate \(\dfrac{da}{dt}=-2\,\dfrac{\text{m}}{\text{sec}}\), how fast is the base moving away from the wall when the top of the ladder is \(a=3\,\text{m}\) above the ground?

    

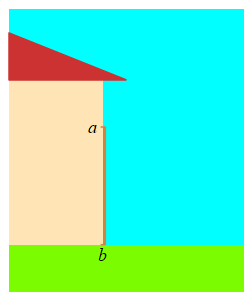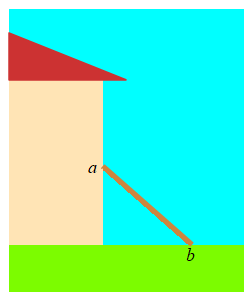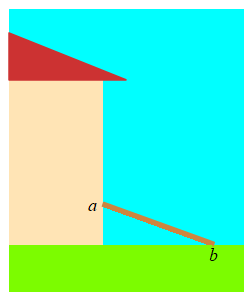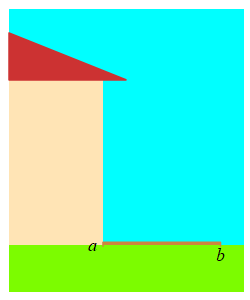
    Use the Pythagorean Theorem. Notice that \(\dfrac{da}{dt}\) is negative. This is because the ladder is sliding down the wall, not up it.

    \(\displaystyle \dfrac{db}{dt}=\dfrac{3}{2}\,\dfrac{\text{m}}{\text{sec}}\)

    \(a\) and \(b\) are related by the Pythagorean Theorem: \[ a^2+b^2=25 \] So when \(a=3\), we have \(b=4\). We differentiate the Pythagorean Theorem, and solve for \(\dfrac{db}{dt}\): \[ 2a\dfrac{da}{dt}+2b\dfrac{db}{dt}=0 \] \[ \dfrac{db}{dt}=-\,\dfrac{a}{b}\,\dfrac{da}{dt} \] Finally, we plug in numbers: \[ \dfrac{db}{dt}=-\,\dfrac{3}{4}(-2)=\dfrac{3}{2}\,\dfrac{\text{m}}{\text{sec}} \]

13. A spherical balloon currently a radius of \(r=8\,\text{cm}\). The balloon is deflating at a rate of \(2\,\dfrac{\text{cm}^3}{\text{sec}}\). How fast is the radius decreasing?

    

    The volume is decreasing.

    \(\dfrac{dr}{dt}= -\,\dfrac{1}{128\pi}\,\dfrac{\text{cm}}{\text{sec}}\)
    So the radius is decreasing at \(\dfrac{1}{128\pi}\,\dfrac{\text{cm}}{\text{sec}}\).

    The volume of a sphere is \(V=\dfrac{4}{3}\pi r^3\). We differentiate and solve for \(\dfrac{dr}{dt}\): \[\begin{aligned} \dfrac{dV}{dt}&=4\pi r^2\dfrac{dr}{dt} \\ \dfrac{dr}{dt}&=\dfrac{1}{4\pi r^2}\dfrac{dV}{dt} \\ &=\dfrac{1}{4\pi(8)^2}\left(-2\right) =-\,\dfrac{1}{128\pi}\,\dfrac{\text{cm}}{\text{sec}} \end{aligned}\] Notice that \(\dfrac{dV}{dt}\) is negative because the volume is decreasing. So the radius is also decreasing at \(\dfrac{1}{128\pi}\,\dfrac{\text{cm}}{\text{sec}}\).

    tj 

14. A baseball diamond is a square with side length \(90 \,\text{ft}\). A baseball player is running from home plate to first base at a speed of \(5 \,\dfrac{\text{ft}}{\text{sec}}\). How fast is the distance between the runner and second base changing when she is halfway to first base?

    

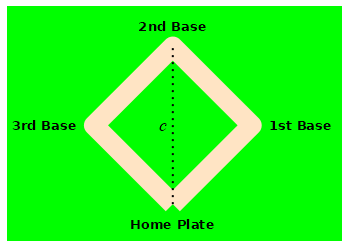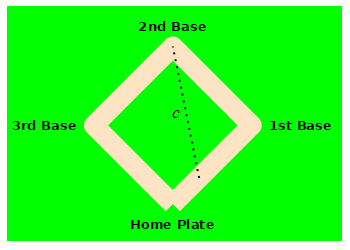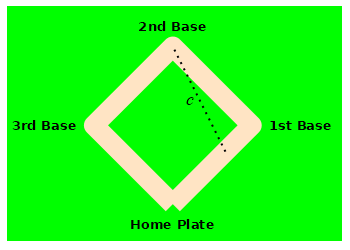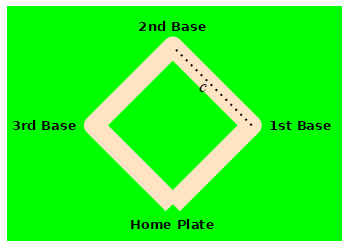
    Use the Pythagorean theorem.

    The distance between the runner and second plate is decreasing at \(\dfrac{dc}{dt}=-\sqrt{5}\,\dfrac{\text{ft}}{\text{sec}}\).

    Let \(a\) be the distance from the runner to first base, \(b\) be the distance from first base to second base and \(c\) be the distance from second base to the runner. By the Pythagorean Theorem: \[ c^2=a^2+b^2=a^2+90^2 \] We differentiate this and solve for \(\dfrac{dc}{dt}\): \[\begin{aligned} 2c\dfrac{dc}{dt}&=2a\dfrac{da}{dt} \\ \dfrac{dc}{dt}&=\dfrac{a}{c}\dfrac{da}{dt} \end{aligned}\]

    

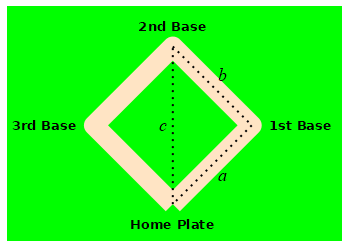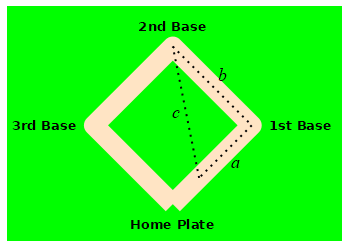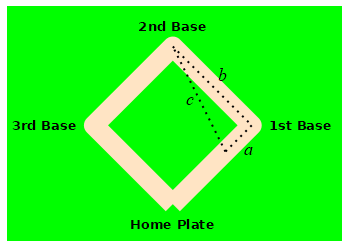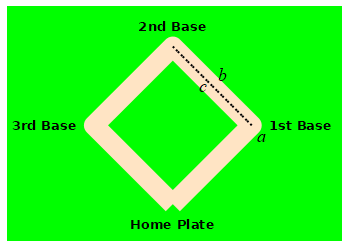
    From the problem \(a=45 \text{ft}\) and \(\dfrac{da}{dt}=-5 \,\dfrac{\text{ft}}{\text{sec}}\). (The minus is because the distance \(a\) is decreasing.) We need to find \(c\): \[\begin{aligned} c^2&=45^2+90^2 \\ c&=\sqrt{45^2+90^2}=45\sqrt{5} \end{aligned}\] Now, we plug in: \[ \dfrac{dc}{dt}=\dfrac{45}{45\sqrt{5}}(-5) =-\sqrt{5}\,\dfrac{\text{ft}}{\text{sec}} \]

15. A cat is drinking milk from a cylindrical bowl. The height of the milk is going down at a rate of \(2\,\dfrac{\text{mm}}{\text{sec}}\). If the bowl has a radius of \(6\, \text{cm}\), how fast is the volume of the milk left in the bowl decreasing?

    

    Remember to convert from mm to cm.

    \(\dfrac{dV}{dt}=-7.2\pi\,\dfrac{\text{cm}^3}{\text{sec}}\)
    So the volume is decreasing at \(7.2\pi\,\dfrac{\text{cm}^3}{\text{sec}}\).

    The volume of a cylinder is \(V=\pi r^2 h\). We plug in the radius and differentiate: \[ V=36\pi h \] \[ \dfrac{dV}{dt}=36\pi\dfrac{dh}{dt} \] We need to convert the rate the height is changing from mm to cm. So \[ \dfrac{dh}{dt}=-0.2 \dfrac{\text{cm}}{\text{sec}} \] Therefore the volume is changing at: \[ \dfrac{dV}{dt}=-36\pi0.2 =-7.2\pi\,\dfrac{\text{cm}^3}{\text{sec}} \] So the volume is decreasing at \(7.2\pi\,\dfrac{\text{cm}^3}{\text{sec}}\).

    tj 

16. A car is \(3\,\text{mi}\) east of an intersection moving east at an unknown speed. The speed limit is \(60\,\text{mph}\). A police car is \(4\,\text{mi}\) south of the intersection moving north at \(60\,\text{mph}\). The officer's radar gun indicates \(90\,\text{mph}\) when pointed at the other car. (That means the straight-line distance between the cars is increasing at \(90\,\text{mph}\).) How fast is the other car moving? Is it speeding?

    

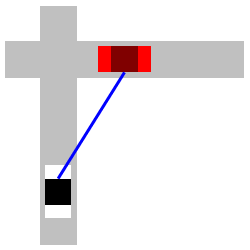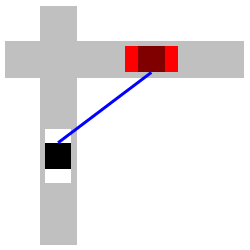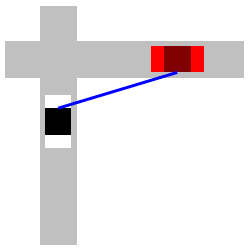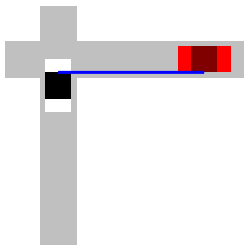
    Start with the Pythagorean Theoerem.

    The other car is speeding at \(70\,\text{mph}\).

    Let \(a\) be the distance from the police car to the intersection and let \(b\) be the distance from the intersection to the other car. Then the distance between the cars, \(c\), is given by the Pythagorean Theoerem, \(c^2=a^2+b^2\). We differentiate: \[ 2c\dfrac{dc}{dt}=2a\dfrac{da}{dt}+2b\dfrac{db}{dt} \] We know \(a=4\) and \(b=3\). So: \(c=\sqrt{3^2+4^2}=5\). We also know \(\dfrac{da}{dt}=60\,\text{mph}\) and \(\dfrac{dc}{dt}=90\,\text{mph}\). We cancel a \(2\) and plug in: \[ (5)(90)=(4)(60)+(3)\dfrac{db}{dt} \] Finally, we solve: \[ \dfrac{db}{dt}=\dfrac{1}{3}(450-240)=\dfrac{210}{3}=70\,\text{mph} \] So, the other car is moving at \(70\,\text{mph}\) which is speeding.

17. The area of a rectangle is staying constant at \(A=30\,\text{cm}^2\). Its length, \(L\) is increasing at a rate of \(\dfrac{dL}{dt}=4\,\dfrac{\text{cm}}{\text{sec}}\). How fast is its width, \(W\), changing when the length is \(L=6\,\text{cm}\)? Is the width increasing or decreasing?

    

    \(W\) is decreasing at \(\dfrac{dW}{dt}=-\,\dfrac{10}{3}\dfrac{\text{cm}}{\text{sec}}\).

    The area of a rectangle is \(A=LW\). Since the area is \(A=30\,\text{cm}^2\) and the length is currently \(L=6\,\text{cm}\), the width is curently: \[ W=\dfrac{A}{L}=\dfrac{30}{6}=5\,\text{cm} \] We differentiate \(A=LW\), and plug in numbers to get: \[ \dfrac{dA}{dt}=W\dfrac{dL}{dt}+L\dfrac{dW}{dt} \] \[ 0=5(4)+6\dfrac{dW}{dt} \] We solve to get: \[ \dfrac{dW}{dt}=-\,\dfrac{20}{6} =-\,\dfrac{10}{3}\,\dfrac{\text{cm}}{\text{sec}} \] So the width is decreasing.

18. Water is evaporating from a circular swimming pool at a rate of \(4\,\dfrac{\text{cm}^3}{\text{hr}}\). At the same time water is flowing in at a rate of \(2\,\dfrac{\text{cm}^3}{\text{hr}}\). If the swimming pool has a radius of \(20\,\text{m}\), how fast is the height decreasing? Assume the swimming pool has the shape of a cylinder with uniform depth, \(h\).

    

    Don't forget to convert units.

    So the height is decreasing at:
    \(\dfrac{\rule{0pt}{10pt}dh}{dt} =-\,\dfrac{1}{2\pi}\times10^{-6}\dfrac{\text{cm}}{\text{hr}} \approx-1.59\times10^{-7}\dfrac{\text{cm}}{\text{hr}}\)

    We first find the value of \(\dfrac{dV}{dt}\): \[ \dfrac{dV}{dt}=2\,\dfrac{\text{cm}^3}{\text{hr}}- 4\,\dfrac{\text{cm}^3}{\text{hr}}=-2\,\dfrac{\text{cm}^3}{\text{hr}} \] Notice the rate is negative because more water is evaporating than flowing in. We also convert the radius from \(\text{m}\) to \(\text{cm}\): \[ r=20\,\text{m}=2000\,\text{cm}=2\times10^{3}\,\text{cm} \] The volume of a cylinder is \(V=\pi r^2 h\). We plug in the radius and differentiate: \[\begin{aligned} V&=4\times10^{6}\pi\,h \\ \dfrac{dV}{dt}&=4\times10^{6}\pi\,\dfrac{dh}{dt} \\ \end{aligned}\] We solve for the rate of change of the height: \[\begin{aligned} \dfrac{dh}{dt}&=\dfrac{1}{4\times10^{6}\pi}\dfrac{dV}{dt} =-\,\dfrac{2}{4\times10^{6}\pi} \\ &=-\,\dfrac{1}{2\pi}\times10^{-6} \approx-1.59\times10^{-7}\dfrac{\text{cm}}{\text{hr}} \end{aligned}\] So the height is decreasing at approximately \(1.59\times10^{-7}\dfrac{\text{cm}}{\text{hr}}\).

    tj 

PY: Checked plots to here

Review Exercises

19. The equation \(h^3k-4h^2k+2hk^3=30\) relates variables \(h\) and \(k\). If \(\dfrac{dh}{dt}=3\), what is \(\dfrac{dk}{dt}\) when \(h=3\) and \(k=2\)?

    \(\dfrac{dk}{dt}=-\,\dfrac{22}{21}\)

    We differentiate using the Chain Rule and the Product Rule: \[\begin{aligned} 3h^2k\dfrac{dh}{dt}+h^3\dfrac{dk}{dt}-8hk\dfrac{dh}{dt}\qquad& \\ -4h^2\dfrac{dk}{dt}+2k^3\dfrac{dh}{dt}+6hk^2\dfrac{dk}{dt}&=0 \\ \left[\rule{0pt}{10pt}3h^2k-8hk+2k^3\right]\dfrac{dh}{dt}\qquad& \\ +\left[\rule{0pt}{10pt}h^3-4h^2+6hk^2\right]\dfrac{dk}{dt}&=0 \end{aligned}\] We plug in and solve: \[\begin{aligned} \left[\rule{0pt}{10pt}3(3)^2(2)-8(3)(2)+2(2)^3\right](3)\qquad& \\ +\left[\rule{0pt}{10pt}(3)^3-4(3)^2+6(3)(2)^2\right]\dfrac{dk}{dt}&=0 \\ 22(3)+63\dfrac{dk}{dt}&=0 \\ \dfrac{dk}{dt}&=-\,\dfrac{22}{21} \end{aligned}\]

    tj 

20. Some water is being boiled in a cylindrical pot with a radius of \(3\,\text{in}\). The height is going down at a rate of \(0.2\dfrac{\text{in}}{\text{min}}\). How fast is the volume decreasing?

    

    \(\dfrac{dV}{dt}=1.8\pi \dfrac{\text{in}^3}{\text{min}}\)

    The volume of the cylindrical pot is \(V=\pi r^2 h\). We plug in the radius and differentiate: \[ V=9\pi h \,\text{in}^2 \] \[\begin{aligned} \dfrac{dV}{dt}&=9\pi \,\text{in}^2 \dfrac{dh}{dt} \\ &=1.8\pi \dfrac{\text{in}^3}{\text{min}} \end{aligned}\]

    tj 

21. A glass of milk is spilled on the floor. It forms a circular puddle in the shape of a cylinder. The radius is currently \(6\,\text{cm}\) and the height is currently \(0.5\,\text{cm}\). Find the rate the height is decreasing if the radius is increasing at \(0.4 \dfrac{\text{cm}}{\text{sec}}\), assuming a constant volume.

    

    So the height is decreasing at
    \(\dfrac{\rule{0pt}{10pt}dh}{dt}=-\,\dfrac{1}{15}\dfrac{\text{cm}}{\text{sec}}\)

    The volume of a cylinder is \(V=\pi r^2 h\). So: \[ \dfrac{dV}{dt}=2\pi r h \dfrac{dr}{dt}+ \pi r^2 \dfrac{dh}{dt} \] Since the amount of milk does not change, the volume does not change. We plug in numbers: \[ 0=2\pi(6)(.5)(.4)+\pi(6)^2\dfrac{dh}{dt} \] And solve for \(\dfrac{dh}{dt}\): \[ 0=2.4+36\dfrac{dh}{dt} \] \[ \dfrac{dh}{dt}=-\,\dfrac{1}{15}\dfrac{\text{cm}}{\text{sec}} \] So the height is decreasing at \(\dfrac{1}{15}\dfrac{\text{cm}}{\text{sec}}\).

    tj 

22. A conical cup with height \(H=10\,\text{cm}\) and radius \(R=2\,\text{cm}\) is being filled up with water at a rate of \(8\,\dfrac{\text{cm}^3}{\text{sec}}\). How fast is the height of the water increasing when it is \(5\,\text{cm}\) deep?

    

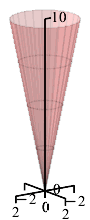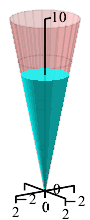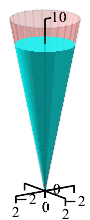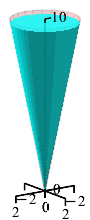
    The volume of a cone is \(V=\dfrac{1}{3}\pi r^2h\). Use similar triangles.

    \(\displaystyle\dfrac{dh}{dt}=\dfrac{8}{\pi}\dfrac{\text{cm}}{\text{sec}}\)

    We start with the volume of a cone: \[ V=\dfrac{1}{3}\pi r^2h \] By similar triangles, the ratio between the height of the water and the radius of the water is: \[ \dfrac{r}{h}=\dfrac{R}{H}=\dfrac{2}{10}=\dfrac{1}{5} \] This means that we can replace \(r=\dfrac{1}{5}h\): \[ V=\dfrac{1}{75}\pi h^3 \] We take the derivative: \[ \dfrac{dV}{dt}=\dfrac{1}{25}\pi h^2\dfrac{dh}{dt} \] The current height is \(5\,\text{cm}\) and the volume is increasing at \(\dfrac{dV}{dt}=8\,\dfrac{\text{cm}^3}{\text{sec}}\). We plug in and solve for the rate of change of the height: \[ 8=\dfrac{1}{25}\pi 5^2\dfrac{dh}{dt} \] \[ \dfrac{dh}{dt}=\dfrac{8}{\pi} \] So, the height is increasing at a speed of \(\dfrac{dh}{dt}=\dfrac{8}{\pi}\,\dfrac{\text{cm}}{\text{sec}}\).