19. Properties of Graphs

b. Value & Limit Information

1. Intercepts & Positive and Negative Values

We start by identifying where the function is positive, negative or zero and where it crosses the $y$ -axis.

Intercepts
An $x$ -intercept of $f(x)$ is a point where the graph crosses the $x$ -axis.
A $y$ -intercept of $f(x)$ is a point where the graph crosses the $y$ -axis.

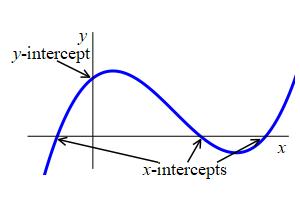
To find the $x$ -intercepts, we solve the equation $f(x)=0$ . There can be zero, one or many $x$ -intercepts.

To find the $y$ -intercepts, we simply plug $x=0$ into the function, i.e. the $y$ -intercept is $f(0)$ if it is defined. There is at most one $y$ -intercept.

Consider the function $f(x)=2x-\dfrac{16}{x-2}$ . First find any points where the function is undefined. Then find the $x$ -intercepts, the $y$ -intercept and the intervals where $f(x)$ is positive or negative.

We first notice that the function is undefined at $x=2$ . Next, to find the $x$ -intercepts, we rewrite the function as: $f(x)=\dfrac{2x(x-2)-16}{x-2}=\dfrac{2x^2-4x-16}{x-2}=\dfrac{2(x+2)(x-4)}{x-2}$ A fraction can only be $0$ if the numerator is $0$ . So, we solve $2(x+2)(x-4)=0$ . So the $x$ -intercepts are $x=-2$ and $x=4$ .
To find the $y$ -intercepts, we plug in $x=0$ : $f(0)=\dfrac{2(0+2)(0-4)}{0-2}=8$ To determine where $f(x)$ is positive or negative, we first plot the interesting points on a number line. These are the $x$ -intercepts, $x=-2$ and $x=4$ , and the places where function is undefined, $x=2$ : eg_2x-16_(x-2)_number_line_crit Since $f$ is continuous except where it is undefined, its sign cannot change without passing through $0$ or a point where it is undefined. So there must be a single sign on each of the intervals $(-\infty,-2)$ , $(-2,2)$ , $(2,4)$ and $(4,\infty)$ . We can find the signs by plugging in a number in each interval: $\begin{aligned} f(-3)&=\dfrac{2(-3+2)(-3-4)}{-3-2}=-\,\dfrac{14}{5} \quad & f(0)&=\dfrac{2(0+2)(0-4)}{0-2}=8 \\ f(3)&=\dfrac{2(3+2)(3-4)}{3-2}=-10 & f(5)&=\dfrac{2(5+2)(5-4)}{5-2}=\dfrac{14}{3} \end{aligned}$ So $f$ is positive on the intervals $(-2,2)$ and $(4,\infty)$ . And $f$ is negative on the intervals $(-\infty,-2)$ and $(2,4)$ . We add these facts to the number line: eg_2x-16_(x-2)_number_line_signs

We will eventually have enough information to plot the function. But so far we can see the $x$ -intercepts at $x=-2$ and $x=4$ , the $y$ -intercept at $y=8$ and the function is positive on $(-2,2)$ and $(4,\infty)$ and negative on $(-\infty,-2)$ and $(2,4)$ . It remains to examine the behavior at $x=\pm\infty$ and $y=\pm\infty$ , to show the function is everywhere increasing, concave up on the left, concave down on the right, and has no local maxima or minima.

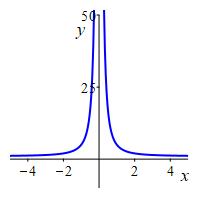
Consider the function $f(x)=1+\dfrac{4}{x^2}$ . First find any points where the function is undefined. Then find the $x$ -intercepts, the $y$ -intercept and the intervals where $f(x)$ is positive or negative. Finally, draw a number line which shows the $x$ -intercepts (marked by a $\bullet$ ), the points where the function is undefined (marked by an $\times$ ) and the signs of the function between these points.

Answer

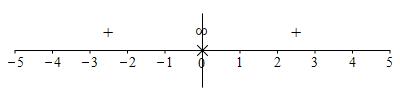
The function is undefined at $x=0$ . There are no $x$ -intercepts nor $y$ -intercept. The function is always positive. ex_1+4_x^2_number_line_signs

[×]

Solution

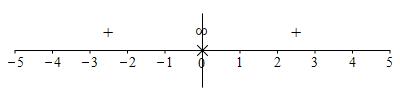
The function is undefined at $x=0$ . So there is no $y$ -intercept. The function is always positive. So there are no $x$ -intercepts. We plot these facts on a number line: ex_1+4_x^2_number_line_signs

[×]

Check

We will eventually have enough information to plot the function. But so far we can see there no intercepts and the function is everywhere positive.

[×]

Consider the function $f(x)=\dfrac{2x^2-10x+12}{x^2-4}$ . First find any points where the function is undefined. Then find the $x$ -intercepts, the $y$ -intercept and the intervals where $f(x)$ is positive or negative. Finally, draw a number line which shows the $x$ -intercepts (marked by a $\bullet$ ), the points where the function is undefined (marked by an $\times$ if it is $\pm\infty$ and an $\circ$ if it is a hole) and the signs of the function between these points.

Answer

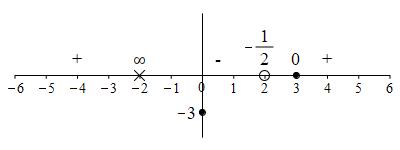
The function is undefined at $x=\pm2$ . $x=2$ is a hole while at $x=-2$ the function approaches $\pm\infty$ . The $x$ -intercept is at $x=3$ . The $y$ -intercept is $f(0)=-3$ . The function is positive on $(-\infty,-2)$ , negative on $(-2,3)$ and positive again on $(3,\infty)$ . ex_2x^2-10x+12_x^2-4_number_line_signs

[×]

Solution

We first factor the numerator and denominator and cancel any common factors: $f(x)=\dfrac{2x^2-10x+12}{x^2-4}=\dfrac{2(x-2)(x-3)}{(x-2)(x+2)} =\dfrac{2(x-3)}{x+2}$ So the function is undefined at $x=\pm2$ because the original denominator is $0$ . However, $x=2$ is a hole because it cancels out and it approaches the finite number: $\lim_{x\to2} f(x)=\lim_{x\to2} \dfrac{2(x-3)}{x+2}=-\,\dfrac{1}{2}$ On the other hand, $x=-2$ is a place where the function approaches $\pm\infty$ since there is a $0$ in the denominator even after factoring. (It is a vertical asymptote which we study on the next page.) The numerator is $0$ when $x=3$ which is the $x$ -intercept. The $y$ -intercept is $f(0)=\dfrac{2(-3)}{2}=-3$ . 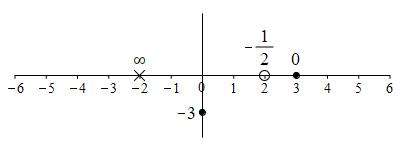We plot these on a number line: ex_2x^2-10x+12_x^2-4_number_line_crit To find where the function is positive or negative, we evaluate if at a point in each interval: $\begin{aligned} f(-4)&=\dfrac{2(-4-3)}{-4+2}=7 \quad & f(0)&=\dfrac{2(-3)}{2}=-3 \\ f(4)&=\dfrac{2(4-3)}{4+2}=\dfrac{1}{3} \end{aligned}$ So the function is positive on $(-\infty,-2)$ , negative on $(-2,3)$ and positive again on $(3,\infty)$ . 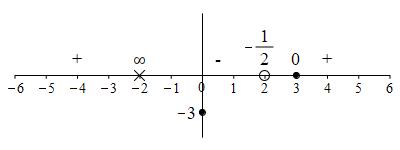ex_2x^2-10x+12_x^2-4_number_line_signs

[×]

Check

We will eventually have enough information to plot the function. But so far we can see the $x$ -intercept at $x=3$ , the $y$ -intercept at $y=-3$ and that the function is positive on $(-\infty,-2)$ and $(3,\infty)$ and negative on $(-2,3)$ .

[×]

19. Properties of Graphs

b. Value & Limit Information

1. Intercepts & Positive and Negative Values

Answer

Solution

Check

Answer

Solution

Check

Heading