7. Computing Limits

d. Limits at Infinity

We have seen the intuitive definitions of limits at a finite number and limits at infinity and how to compute limits at finite numbers. We now look at how to compute limits at infinity. The process is the same as for limits at finite numbers. We first look at a few special limits, then at the Limit Laws and finally what to do when the Limit Laws don't apply. The formal proofs will appear in the chapter on Precise Limits and Continuity.

1. Special Limits

\[ \lim_{x\to\infty}x=\infty \]

prop_id — The identity function \(y=x\).

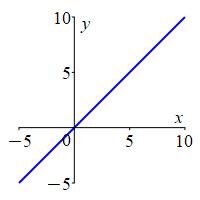
As \(x\) approaches \(\infty\), we conclude \(x\) approaches \(\infty\).

For any number \(c\), \[ \lim_{x\to\infty}c=c \]

prop_const — The constant function \(y=c\).

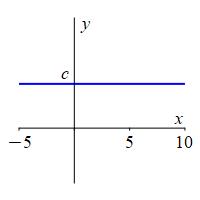
For all \(x\), \(f(x)=c\). So as \(x\) approaches \(\infty\), the value of \(f(x)\) continues to be \(c\).

As an example we have: \[ \lim\limits_{x\to\infty}7=7 \]

If \(p>0\), then \[ \lim_{x\to\infty}x^p=\infty \qquad \text{and} \qquad \lim_{x\to\infty}\dfrac{1}{x^p}=0. \] If \(p<0\), then \[ \lim_{x\to\infty}x^p=0 \qquad \text{and} \qquad \lim_{x\to\infty}\dfrac{1}{x^p}=\infty. \]

prop_power — The power function \(y=x^2\).

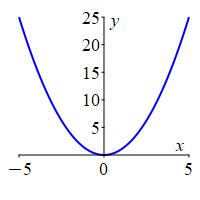
As examples we have: \[\begin{array}{ll} \lim\limits_{x\to\infty}x^2 =\lim\limits_{x\to\infty}\dfrac{1}{x^{-2}}=\infty \qquad & \lim\limits_{x\to\infty}x^{1/2} =\lim\limits_{x\to\infty}\dfrac{1}{x^{-1/2}} =\lim\limits_{x\to\infty}\sqrt{x}=\infty \\ \lim\limits_{x\to\infty}x^{-2} =\lim\limits_{x\to\infty}\dfrac{1}{x^2}=0 \qquad & \lim\limits_{x\to\infty}x^{-1/2} =\lim\limits_{x\to\infty}\dfrac{1}{x^{1/2}} =\lim\limits_{x\to\infty}\dfrac{1}{\sqrt{x}}=0 \end{array}\] To justify these, try plugging in \(x=1\) million, i.e. \(x=1,000,000=10^6\).

If \(b>1\), then \[ \lim_{x\to\infty}b^x=\infty \qquad \text{and} \qquad \lim_{x\to\infty}\dfrac{1}{b^x}=0. \] If \(0 < b < 1\), then \[ \lim_{x\to\infty}b^x=0 \qquad \text{and} \qquad \lim_{x\to\infty}\dfrac{1}{b^x}=\infty. \]

prop_exp — The exponential function \(y=2^x\).

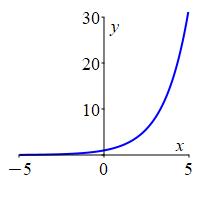
As examples we have: \[\begin{array}{ll} \lim\limits_{x\to\infty}2^x=\infty \qquad &\lim\limits_{x\to\infty}\left(\dfrac{1}{2}\right)^x =\lim\limits_{x\to\infty}\dfrac{1}{2^x}=0 \end{array}\] To justify these, try plugging in \(x=10\) or \(x=20\).

Study the difference between the power and the exponential functions. The first is a limit with a variable base \(x\) to a fixed power \(p\). The second is a limit with a fixed base \(b\) to a variable power \(x\).

7. Computing Limits

d. Limits at Infinity

1. Special Limits

Heading