7. Computing Limits

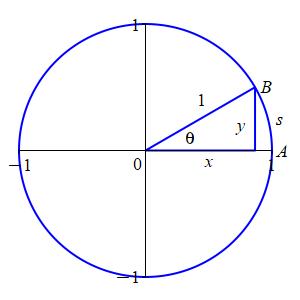
Let's first assume \(\theta\gt0\). The diagram shows a unit circle and a ray at an angle \(\theta\) intersecting the circle at the point \(B=(\cos\theta,\sin\theta)\). The circumference of the full circle is \(2\pi r=2\pi\). The fraction of the circumference occupied by the arc \(\stackrel{\frown}{AB}\) is \(\dfrac{\theta}{2\pi}\) (in radians). So the length of the arc is \(s=\dfrac{\theta}{2\pi}2\pi=\theta\). The perpendicular from \(B\) to the \(x\)-axis has length \(y=\sin\theta\) and since the length of a perpendicular is shortest distance, we conclude \[ 0 \le \sin\theta \le s = \theta \] So \(\sin\theta\) is squeezed between \(0\) and \(\theta\). Since \[ \lim_{\theta\to0^+}0=\lim_{\theta\to0^+}\theta=0 \] we conclude \(\displaystyle \lim_{\theta\to0^+}\sin\theta=0\) also.

Now, let's assume \(\theta\lt0\). We let \(t=-\theta\) and use the fact that \(\sin\) is odd, to compute: \[ \lim_{\theta\to0^-}\sin\theta =\lim_{t\to0^+}\sin(-t) =-\lim_{t\to0^+}\sin(t) =0 \]

This limit does not need the Sandwich Theorem. We just use a trig identity the Limit Laws and the previous limit. \[\begin{aligned} \lim_{\theta\to0}\cos\theta &=\lim_{\theta\to0}\sqrt{1-\sin^2\theta} \\ &=\sqrt{\lim_{\theta\to0}\left(1-\sin^2\theta\right)} \\ &=\sqrt{1-\left(\lim_{\theta\to0}\sin\theta\right)^2} \\ &=\sqrt{1-(0)^2}=1 \\ \end{aligned}\]

The diagram shows a unit circle and a ray at an angle \(\theta\) intersecting the circle at the point \(B=(\cos\theta,\sin\theta)\). The area of the full circle is \(\text{Area}_\bigcirc=\pi r^2=\pi\). The fraction of the area occupied by the sector \(\measuredangle OAB\) is \(\dfrac{\theta}{2\pi}\) (in radians). So the area of the sector is \[ \text{Area}_{\measuredangle OAB}=\dfrac{\theta}{2\pi}\pi=\dfrac{\theta}{2} \] This sector is sandwiched between two triangles. The smaller triangle is \(\triangle OAB\) whose area is \[ \text{Area}_{\triangle OAB}=\dfrac{1}{2}(1)\sin\theta \] The larger triangle is \(\triangle OAC\) whose area is \[ \text{Area}_{\triangle OAC}=\dfrac{1}{2}(1)\tan\theta \]

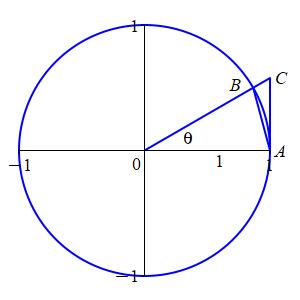
The three areas are related by: \[ \text{Area}_{\triangle OAB} \le \text{Area}_{\measuredangle OAB} \le \text{Area}_{\triangle OAC} \] \[ \dfrac{1}{2}\sin\theta \le \dfrac{\theta}{2} \le \dfrac{1}{2}\tan\theta \] The first inequality can be rearranged to say: \[ \dfrac{\sin\theta}{\theta} \le 1 \] The second inequality can be rearranged to say: \[ 1 \le \dfrac{\tan\theta}{\theta}=\dfrac{\sin\theta}{\theta\cos\theta} \] or \[ \cos\theta \le \dfrac{\sin\theta}{\theta} \] Together, they say \(\dfrac{\sin\theta}{\theta}\) is squeezed between \(\cos\theta\) and \(1\). Since \[ \lim_{\theta\to0}\cos\theta=\lim_{\theta\to0}1=1 \] we conclude \(\displaystyle \lim_{\theta\to0}\dfrac{\sin\theta}{\theta}=1\) also.

This limit does not need the Sandwich Theorem. We multiply by the conjugate, use a trig identity and the previous limits. \[\begin{aligned} \lim_{\theta\to0}\dfrac{1-\cos\theta}{\theta} &=\lim_{\theta\to0}\dfrac{(1-\cos\theta)}{\theta}\dfrac{(1+\cos\theta)}{(1+\cos\theta)} \\ &=\lim_{\theta\to0}\dfrac{(1-\cos^2\theta)}{\theta^2}\dfrac{\theta}{(1+\cos\theta)} \\ &=\lim_{\theta\to0}\dfrac{\sin^2\theta}{\theta^2}\dfrac{\theta}{(1+\cos\theta)} \\ &=\left(\lim_{\theta\to0}\dfrac{\sin\theta}{\theta}\right)^2 \lim_{\theta\to0}\dfrac{\theta}{1+\cos\theta} \\ &=(1)^2\left(\dfrac{0}{1+1}\right)=0 \end{aligned}\]