22. Parametric Surfaces and Surface Integrals

b. Tangent and Normal Vectors

2. Tangent Vectors

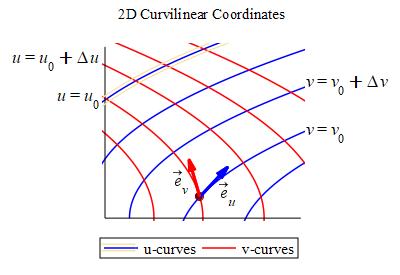
For a 2D curvilinear coordinate system R⃗(u,v)\vec R(u,v), the coordinate tangent vectors are the tangent vectors to the coordinate curves. e⃗u=∂R⃗∂uande⃗v=∂R⃗∂v \vec e_u=\dfrac{\partial\vec R}{\partial u} \qquad \text{and} \qquad \vec e_v=\dfrac{\partial\vec R}{\partial v} e⃗u\vec e_u is tangent to the uu-curves and points in the direction of increasing uu. e⃗v\vec e_v is tangent to the vv-curves and points in the direction of increasing vv. We do the same thing for parametric surfaces:

Coordinate Tangent Vectors
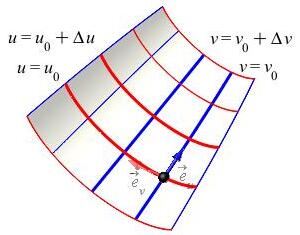
The tangent vector to the uu-curves is e⃗u=∂R⃗∂u=⟨∂x∂u,∂y∂u,∂z∂u⟩ \vec{e}_u=\dfrac{\partial\vec R}{\partial u} =\left\langle \dfrac{\partial x}{\partial u}, \dfrac{\partial y}{\partial u}, \dfrac{\partial z}{\partial u} \right\rangle and points in the direction of increasing uu.
The tangent vector to the vv-curves is e⃗v=∂R⃗∂v=⟨∂x∂v,∂y∂v,∂z∂v⟩ \vec{e}_v=\dfrac{\partial\vec R}{\partial v} =\left\langle \dfrac{\partial x}{\partial v}, \dfrac{\partial y}{\partial v}, \dfrac{\partial z}{\partial v} \right\rangle and points in the direction of increasing vv.
PY: Make the blue vector shorter.

surfgrid-tanvec

The vector e⃗u\vec{e}_u (as well as e⃗v\vec{e}_v) is analogous to the to tangent (or velocity) vector to a parametric curve, r⃗(t)=⟨x(t),y(t),z(t)⟩\vec r(t)=\left\langle x(t),y(t),z(t)\right\rangle, given by: v⃗=dr⃗dt=⟨dxdt,dydt,dzdt⟩ \vec{v}=\dfrac{d\vec r}{dt} =\left\langle \dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle with the following exceptions:

  1. The parameter for R⃗(u,v0)\vec R(u,v_0) is uu rather than tt; so we need to differentiate the with respect to uu.
  2. Since the vv-coordinate is held constant at v0v_0, the derivative needs to be a partial derivative with respect to uu instead of a total derivative with respect to tt.
  3. We do not refer to the tangent vector as a velocity because the parameter, uu, represents a coordinate on the surface, not a time.
  4. We use the symbols e⃗u\vec e_u and e⃗v\vec e_v rather than the letter v⃗\vec{v} for the tangent vectors, because they are not velocities and also because we have already used vv for a parameter.

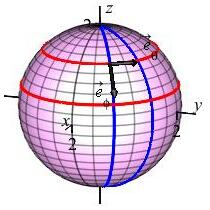
Find the tangent vectors to the sphere of radius ρ=2\rho=2, parametrized by: R⃗(ϕ,θ)=⟨2sin⁡ϕcos⁡θ,2sin⁡ϕsin⁡θ,2cos⁡ϕ⟩ \vec R(\phi,\theta) =\left\langle 2\sin\phi\cos\theta,2\sin\phi\sin\theta,2\cos\phi\right\rangle PY: Add the tangent vectors to the plot.

Sphere_coordcurves

The tangent vectors to the ϕ\phi and θ\theta curves are e⃗ϕ=∂R⃗∂ϕ=⟨2cos⁡ϕcos⁡θ,2cos⁡ϕsin⁡θ,−2sin⁡ϕ⟩e⃗θ=∂R⃗∂θ=⟨−2sin⁡ϕsin⁡θ,2sin⁡ϕcos⁡θ,0⟩\begin{aligned} \vec{e}_\phi&=\dfrac{\partial\vec R}{\partial\phi} =\left\langle 2\cos\phi\cos\theta,2\cos\phi\sin\theta,-2\sin\phi\right\rangle \\ \vec{e}_\theta&=\dfrac{\partial\vec R}{\partial\theta} =\left\langle -2\sin\phi\sin\theta,2\sin\phi\cos\theta,\quad 0\quad \right\rangle \end{aligned} Notice that e⃗θ\vec{e}_\theta is horizontal since it is tangent to a line of latitude and it points East in the direction of increasing θ\theta. Similarly, e⃗ϕ\vec{e}_\phi points South, tangent to a line of longitude, in the direction of increasing ϕ\phi.

Compute the tangent vectors to the elliptic paraboloid z=x2+y2z=x^2+y^2 parametrized by: R⃗(r,θ)=⟨rcos⁡θ,rsin⁡θ,r2⟩ \vec R(r,\theta)=\left\langle r\cos\theta,r\sin\theta,r^2\right\rangle PY: Change the grid on the paraboloid to polar. Add tangent vectors.

EllipticParaboloid2

Answer

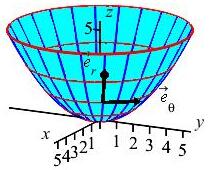
e⃗r=⟨cos⁡θ,sin⁡θ,2r⟩e⃗θ=⟨−rsin⁡θ,rcos⁡θ,0⟩\begin{aligned} \vec e_r&=\left\langle \cos\theta,\sin\theta,2r\right\rangle \\ \vec e_\theta&=\left\langle -r\sin\theta,r\cos\theta,0\right\rangle \end{aligned}

[×]

Solution

We simply compute: e⃗r=∂R⃗∂r=⟨cos⁡θ,sin⁡θ,2r⟩e⃗θ=∂R⃗∂θ=⟨−rsin⁡θ,rcos⁡θ,0⟩\begin{aligned} \vec e_r&=\dfrac{\partial\vec R}{\partial r} =\left\langle \cos\theta,\sin\theta,2r\right\rangle \\ \vec e_\theta&=\dfrac{\partial\vec R}{\partial\theta} =\left\langle -r\sin\theta,r\cos\theta,0\right\rangle \end{aligned}

[×]

Find the tangent vectors to the piece of the cylinder x2+z2=4x^2+z^2=4 between y=0y=0 and y=6+2x+3zy=6+2x+3z parametrized by: R⃗(θ,y)=⟨2cos⁡θ,y,2sin⁡θ⟩ \vec R(\theta,y)=\left\langle 2\cos\theta,y,2\sin\theta\right\rangle PY: Fix the grid to y theta. Add tangent vectors.

Cylinder_exercise2

Answer

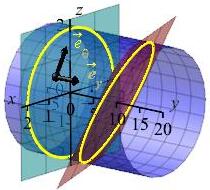
e⃗θ=⟨−2sin⁡θ,0,2cos⁡θ⟩e⃗y=⟨0,1,0⟩\begin{aligned} \vec e_\theta&=\left\langle -2\sin\theta,0,2\cos\theta\right\rangle \\ \vec e_y&=\left\langle 0,1,0\right\rangle \end{aligned}

[×]

Solution

We simply compute: e⃗θ=∂R⃗∂θ=⟨−2sin⁡θ,0,2cos⁡θ⟩e⃗y=∂R⃗∂y=⟨0,1,0⟩\begin{aligned} \vec e_\theta&=\dfrac{\partial\vec R}{\partial\theta} =\left\langle -2\sin\theta,0,2\cos\theta\right\rangle \\ \vec e_y&=\dfrac{\partial\vec R}{\partial y} =\left\langle 0,1,0\right\rangle \end{aligned}

[×]

Remark

Notice the parameter ranges have absolutely nothing to do with the tangent vectors. They only affect the limits of integration.

[×]

© 2025 MYMathApps

Supported in part by NSF Grant #1123255