22. Parametric Surfaces and Surface Integrals
b. Tangent and Normal Vectors
3. Normal Vector
For a parametric curve, the important vector is the tangent vector, \(\vec{v}\).
For a parametric surface, the important vector is the normal vector, \(\vec{N}\).
Since the tangent vectors \(\vec{e}_u\) and \(\vec{e}_v\) are tangent to a parametric surface, the normal vector \(\vec{N}\) can be computed as the cross product of \(\vec{e}_u\) and \(\vec{e}_v\).
The normal vector, \(\vec{N}\), to a parametric surface is: \[\begin{aligned} \vec{N}&=\vec{e}_u\times\vec{e}_v =\left| \begin{array}{ccc} \hat{\imath} & \hat{\jmath} & \hat{k} \\[3pt] \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} & \dfrac{\partial z}{\partial u} \\[8pt] \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} & \dfrac{\partial z}{\partial v} \end{array} \right| \\[5pt] &=\left(\dfrac{\partial y}{\partial u}\dfrac{\partial z}{\partial v}- \dfrac{\partial z}{\partial u}\dfrac{\partial y}{\partial v}\right) \hat{\imath} \\ &\quad-\left(\dfrac{\partial x}{\partial u}\dfrac{\partial z}{\partial v}- \dfrac{\partial z}{\partial u}\dfrac{\partial x}{\partial v}\right) \hat{\jmath} \\ &\qquad+\left(\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v}- \dfrac{\partial y}{\partial u}\dfrac{\partial x}{\partial v}\right) \hat{k} \\[5pt] &=\left\langle \dfrac{\partial(y,z)}{\partial(u,v)}, -\,\dfrac{\partial(x,z)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle \end{aligned}\]
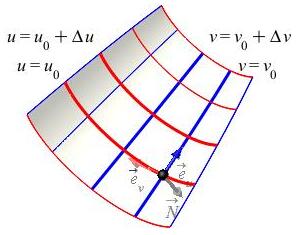
Notice that the components of the normal vector are \(2\)-dimensional Jacobian determinants. For the \(x\) component the variables are \(y\) and \(z\). For the \(y\) component the variables are \(x\) and \(z\). For the \(z\) component the variables are \(x\) and \(y\). Also notice that in each component the variables \(x,y,z\) occur in alphabetical order, \(yz\), \(xz\), \(xy\), but there is a minus on the \(y\) component. However, back up a step and distribute the minus sign in the \(y\) component. Then:
\[\begin{aligned} \vec{N} &=\left(\dfrac{\partial y}{\partial u}\dfrac{\partial z}{\partial v}- \dfrac{\partial z}{\partial u}\dfrac{\partial y}{\partial v}\right) \hat{\imath} +\left(\dfrac{\partial z}{\partial u}\dfrac{\partial x}{\partial v}- \dfrac{\partial x}{\partial u}\dfrac{\partial z}{\partial v}\right) \hat{\jmath} +\left(\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v}- \dfrac{\partial y}{\partial u}\dfrac{\partial x}{\partial v}\right) \hat{k} \\[5pt] &=\left\langle \dfrac{\partial(y,z)}{\partial(u,v)}, \dfrac{\partial(z,x)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle \end{aligned}\]
In this version, there is no minus sign but the variables are now in cyclic order, i.e. \(xyzxyz\cdots\). You can remember \(\vec{N}\) in either version. However, in computing \(\vec{N}\) we rarely use the Jacobian determinants, but rather, go back to the cross product formula.
Caution: We previously saw Jacobian determinants in the computation of the differentials of area and volume. In those cases, the sign of the determinant did not matter because we were taking the absolute value to form the Jacobian factor. However, in computing the components of the normal vector, the sign of each Jacobian determinant is crucial since if you make a mistake, the vector will no longer be normal! This is particularly true for the sign of the \(y\)-component.
In dealing with parametric surfaces, you will have to compute the normal many times and the length of the formulas will keep growing. If you try to copy the components of \(\vec{e}_u\) and \(\vec{e}_v\) to take the cross product, you will invariably make a copying mistake at some time. Don't re-copy. It is a waste of time and leads to mistakes. If you carefully calculate \(\vec{e}_u\) and \(\vec{e}_v\) and keep things lined up, you just need to put the row \(\hat{\imath}\), \(\hat{\jmath}\), \(\hat{k}\) on top of the values of \(\vec{e}_u\) and \(\vec{e}_v\) and take the determinant of the resulting matrix. On paper, your work would look like this. First, compute the two tangent vectors: \[ \begin{array}{c} \\ \vec{e}_u=\dfrac{\partial R}{\partial u}=\, \\[10pt] \vec{e}_v=\dfrac{\partial R}{\partial v}=\, \end{array} \left. \begin{array}{ccc} & & \\[3pt] \left\langle \dfrac{\partial x}{\partial u}\right. & \dfrac{\partial y}{\partial u} & \left. \dfrac{\partial z}{\partial u}\right\rangle\\[10pt] \left\langle \dfrac{\partial x}{\partial v}\right. & \dfrac{\partial y}{\partial v} & \left. \dfrac{\partial z}{\partial v}\right\rangle \end{array} \right. \] Now add an \(\hat{\imath}\), \(\hat{\jmath}\) and \(\hat{k}\) and some vertical bars and compute the determinant. Click Here to add the determinant.
On the next page, we will see that it is also useful to know the length of the normal vector. So these examples and exercises also ask for the length.
Find the normal vector to the sphere of radius \(\rho=2\), parametrized by \[ \vec R(\phi,\theta) =\left\langle 2\sin\phi\cos\theta,2\sin\phi\sin\theta,2\cos\phi\right\rangle \] Then find the magnitude of the normal.
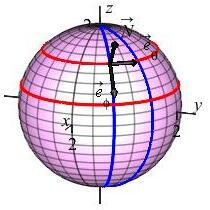
We previously found the tangent vectors: \[\begin{aligned} \vec{e}_\phi&=\dfrac{\partial\vec R}{\partial\phi} =\left\langle 2\cos\phi\cos\theta,2\cos\phi\sin\theta,-2\sin\phi\right\rangle \\ \vec{e}_\theta&=\dfrac{\partial\vec R}{\partial\theta} =\left\langle -2\sin\phi\sin\theta,2\sin\phi\cos\theta,\quad 0\quad \right\rangle \end{aligned}\] Now add the \(\hat{\imath}\), \(\hat{\jmath}\), \(\hat{k}\) and some vertical bars and complete the computation of the cross product: \[\begin{aligned} \vec{N}&=\vec{e}_\phi\times\vec{e}_\theta =\left| \begin{array}{ccc} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \left\langle 2\cos\phi\cos\theta\right. & 2\cos\phi\sin\theta& \left. -2\sin\phi\right\rangle\\ \left\langle -2\sin\phi\sin\theta\right. & 2\sin\phi\cos\theta& \left. \quad 0\quad\right\rangle \end{array} \right| \\ &=\hat{\imath}(0+4\sin^2\phi\cos\theta) -\hat{\jmath}(0-4\sin^2\phi\sin\theta) \\ & \qquad+\hat{k}(4\sin\phi\cos\phi\cos^2\theta+4\sin\phi\cos\phi\sin^2\theta) \\ &=\left\langle 4\sin^2\phi\cos\theta, 4\sin^2\phi\sin\theta, 4\sin\phi\cos\phi\right\rangle \end{aligned}\]
Notice that \(\vec{N}\) points in the same direction as the position vector since \(\vec{N}=2\sin\phi\,\vec R(\phi,\theta)\). This should be expected since the position vector from the origin to the sphere is perpendicular to the surface.
This result is the normal vector. Its magnitude will also be useful in doing integrals. So we compute: \[\begin{aligned} |\vec{N}| &=\sqrt{(4\sin^2\phi\cos\theta)^2+(4\sin^2\phi\sin\theta)^2+(4\sin\phi\cos\phi)^2} \\ &=\sqrt{16\sin^4\phi\cos^2\theta+16\sin^4\phi\sin^2\theta+16\sin^2\phi\cos^2\phi} \\ &=\sqrt{16\sin^4\phi+16\sin^2\phi\cos^2\phi} =\sqrt{16\sin^2\phi(\sin^2\phi+\cos^2\phi)} \\ &=\sqrt{16\sin^2\phi}=4\sin\phi \end{aligned}\]
Notice this result resembles the Jacobian factor for spherical coordinates: \(J=\rho^2\sin\phi\). This is coincidence for the spherical geometry.
Find the tangent vectors, normal vector, and length of the normal vector for the hyperbolic paraboloid \(z=\dfrac{x^2-y^2}{5}\) discussed in a previous exercise and parametrized by: \(\vec R(r,\theta) =\left\langle r\cos\theta,r\sin\theta, \dfrac{r^2}{5}(\cos^2\theta-\sin^2\theta)\right\rangle\)
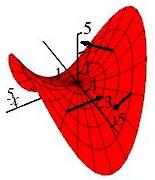
The tangent vectors are:
\(\begin{aligned}
\vec{e}_r
&=\left\langle \cos\theta,\sin\theta,
\dfrac{2r}{5}(\cos^2\theta-\sin^2\theta)\right\rangle \\
\vec{e}_\theta
&=\left\langle -r\sin\theta,r\cos\theta,
\dfrac{r^2}{5}(-4\sin\theta\cos\theta)\right\rangle
\end{aligned}\)
The normal vector is:
\(\vec{N}=\left\langle -\,\dfrac{2r^2}{5}\cos\theta,\dfrac{2r^2}{5}\sin\theta,
r\right\rangle\)
Its length is:
\(|\vec{N}|=\sqrt{\dfrac{4r^4}{25}+r^2}\)
To find the tangent vectors, we take the derivative of the parametrization with respect to the two parameters: \[\begin{aligned} \vec{e}_r &=\dfrac{\partial\vec R}{\partial r} =\left\langle \cos\theta,\sin\theta, \dfrac{2r}{5}(\cos^2\theta-\sin^2\theta)\right\rangle \\ \vec{e}_\theta &=\dfrac{\partial\vec R}{\partial\theta} =\left\langle -r\sin\theta,r\cos\theta, \dfrac{r^2}{5}(-4\sin\theta\cos\theta)\right\rangle \end{aligned}\] To find the normal vector we compute the cross product of the two tangent vectors: (On paper, don't recopy the tangent vectors; just add \(\hat{\imath}\), \(\hat{\jmath}\) and \(\hat{k}\) and vertical bars.) \[\begin{aligned} \vec{N} &=\vec{e}_r\times\vec{e}_\theta =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos\theta & \sin\theta & \dfrac{2r}{5}(\cos^2\theta-\sin^2\theta) \\ -r\sin\theta & r\cos\theta & \dfrac{r^2}{5}(-4\sin\theta\cos\theta) \end{vmatrix} \\ &=\hat{\imath}(-\,\dfrac{4r^2}{5}\sin^2\theta\cos\theta -\dfrac{2r^2}{5}\cos^3\theta+\dfrac{2r^2}{5}\cos\theta\sin^2\theta) \\ &\qquad-\,\hat{\jmath}(-\,\dfrac{4r^2}{5}\sin\theta\cos^2\theta +\dfrac{2r^2}{5}\sin\theta\cos^2\theta-\dfrac{2r^2}{5}\sin^3\theta) \\ &\qquad+\hat{k}(r\cos^2\theta+r\sin^2\theta) \\ &=\hat{\imath}(-\,\dfrac{2r^2}{5}\sin^2\theta\cos\theta-\dfrac{2r^2}{5}\cos^3\theta) \\ &\qquad-\,\hat{\jmath}(-\,\dfrac{2r^2}{5}\sin\theta\cos^2\theta-\dfrac{2r^2}{5}\sin^3\theta)+\hat{k}(r) \\ &=\hat{\imath}(-\,\dfrac{2r^2}{5}\cos\theta)-\hat{\jmath}(-\,\dfrac{2r^2}{5}\sin\theta)+\hat{k}(r) \\ &=\left\langle -\,\dfrac{2r^2}{5}\cos\theta,\dfrac{2r^2}{5}\sin\theta,r\right\rangle \end{aligned}\] Finally, its length is: \[ |\vec{N}| =\sqrt{\left(\dfrac{2r^2}{5}\cos\theta\right)^2 +\left(\dfrac{2r^2}{5}\sin\theta\right)^2+r^2} =\sqrt{\dfrac{4r^4}{25}+r^2} \]
We can check the normal vector by computing its dot product with each tangent vector: \[\begin{aligned} \vec{N}\cdot\vec{e}_r &=-\,\dfrac{2r^2}{5}\cos^2\theta+\dfrac{2r^2}{5}\sin^2\theta +\dfrac{2r^2}{5}(\cos^2\theta-\sin^2\theta) \\ &=0 \\ \vec{N}\cdot\vec{e}_\theta &=\dfrac{2r^3}{5}\cos\theta\sin\theta+\dfrac{2r^3}{5}\sin\theta\cos\theta +\dfrac{r^3}{5}(-4\sin\theta\cos\theta) \\ &=0 \end{aligned}\]
Find the normal vector, and length of the normal vector for the cylinder \(x^2+z^2=4\) discussed in two previous exercises and parametrized by \(\vec R(\theta,y)=\left\langle 2\cos\theta,y,2\sin\theta\right\rangle\).
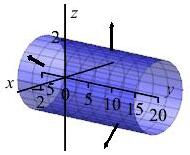
The normal vector is:
\(\vec{N}=\left\langle -2\cos\theta,0,-2\sin\theta\right\rangle\)
Its length is:
\(|\vec{N}|=2\)
We previously found the tangent vectors: \[\begin{aligned} \vec{e}_\theta &=\dfrac{\partial\vec R}{\partial\theta} =\left\langle -2\sin\theta,0,2\cos\theta\right\rangle \\ \vec{e}_y &=\dfrac{\partial\vec R}{\partial y} =\left\langle 0,1,0\right\rangle \end{aligned}\] Again, to find the normal vector we compute the cross product of the two tangent vectors: \[\begin{aligned} \vec{N} &=\vec{e}_\theta\times\vec{e}_y =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ -2\sin\theta & 0 & 2\cos\theta\\ 0 & 1 & 0 \end{vmatrix} \\ &=\hat{\imath}(0-2\cos\theta) -\hat{\jmath}(0-0) +\hat{k}(-2\sin\theta) \\ &=\left\langle -2\cos\theta,0,-2\sin\theta\right\rangle \end{aligned}\] Finally, its length is: \[ |\vec{N}|=\sqrt{\left(2\cos\theta\right)^2+0+\left(-2\sin\theta\right)^2}=2 \]
We can check the normal vector by computing its dot product with each tangent vector: \[\begin{aligned} \vec{N}\cdot\vec{e}_\theta &=4\cos\theta\sin\theta-4\sin\theta\cos\theta \\ &=0 \\ \vec{N}\cdot\vec{e}_y &=-2\cos\theta\cdot0+0\cdot1-2\sin\theta\cdot0 \\ &=0 \end{aligned}\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum