5. Partial Derivatives and Tangent Planes
Exercises
-
\(f(x,y)=x^2y+xy^2\)
-
\(f_x\)
\(y\) is a constant.
\(f_x=2xy+y^2\)
We differentiate \(f(x,y)\) with respect to \(x\) assuming \(y\) is a constant: \[ f_x=\dfrac{\partial}{\partial x}(x^2y+xy^2)=2xy+y^2 \]
dm,jb
-
\(f_y\)
This time, \(x\) is a constant.
\(f_y=x^2+2xy\)
We differentiate \(f(x,y)\) with respect to \(y\) assuming \(x\) is a constant: \[ f_y=\dfrac{\partial}{\partial y}(x^2y+xy^2)=x^2+2xy \]
gg
-
-
\(g(x,y)=y\sin x+x\sin y+\sin(xy)+2\)
-
\(\dfrac{\partial g}{\partial x}\)
\(y\) is a constant.
\(\dfrac{\partial g}{\partial x}=y\cos x+\sin y+y\cos(xy)\)
To find \(\dfrac{\partial g}{\partial x}\), we differentiate \(g(x,y)\) with respect to \(x\), while keeping \(y\) constant: \[ \dfrac{\partial g}{\partial x}=y\cos x+\sin y+y\cos(xy) \]
dm,jb,gg
-
\(\dfrac{\partial g}{\partial y}\)
\(\dfrac{\partial g}{\partial y}=\sin x+x\cos y+x\cos(xy)\)
We find \(\dfrac{\partial g}{\partial y}\) by differentiating \(g(x,y)\) with respect to \(y\), while keeping \(x\) constant: \[ \dfrac{\partial g}{\partial y}=\sin x+x\cos y+x\cos(xy) \]
dm,jb,gg
-
-
\(h=x(\ln y)\sin(xy)+\cos(xy)\).
-
\(\partial_x h\)
\(\partial_x h=(\ln y)\sin(xy)+xy(\ln y)\cos(xy)-y\sin(xy)\)
We differentiate \(h\) with respect to \(x\) holding \(y\) constant: \[ \partial_x h=(\ln y)\sin(xy)+xy(\ln y)\cos(xy)-y\sin(xy) \]
dm
-
\(\partial_y h\)
\(\partial_y h=\dfrac{x\sin(xy)}{y}+x^2(\ln y)\cos(xy)-x\sin(xy)\)
We differentiate \(h\) with respect to \(y\) holding \(x\) constant: \[ \partial_x h=\dfrac{x\sin(xy)}{y}+x^2(\ln y)\cos(xy)-x\sin(xy) \]
dm
-
-
\(r(p,q)=pe^{pq}\)
-
\(\dfrac{\partial r}{\partial q}\)
\(p\) is constant.
\(\dfrac{\partial r}{\partial q}= p^2e^{pq}\)
We differentiate \(r\) with respect to \(q\) holding \(p\) constant: \[ \dfrac{\partial r}{\partial q}=\dfrac{\partial}{\partial q} \left(pe^{pq}\right) = p^2e^{pq} \]
gg
-
\(\dfrac{\partial r}{\partial p}\)
\(\dfrac{\partial r}{\partial p}= e^{pq}+pqe^{pq}\)
We differentiate \(r\) with respect to \(p\) holding \(q\) constant. For this we will use the Product Rule: \[ \dfrac{\partial r}{\partial p}=\dfrac{\partial}{\partial p} \left(pe^{pq}\right) = e^{pq}+pqe^{pq} \]
gg
-
-
Find the \(x\)-partial derivative of \(f(x,y)=x^2y^3\) using the limit definition of partial derivatives.
\(f_x(x,y)=2xy^3\)
According to the algebraic definition of partial derivatives: \[\begin{aligned} f_x(x,y) &=\lim_{h\rightarrow 0} \dfrac{f(x+h,y)-f(x,y)}{h} =\lim_{h\rightarrow 0} \dfrac{(x+h)^2y^3-x^2y^3}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{(x^2+2hx+h^2)y^3-x^2y^3}{h} =\lim_{h\rightarrow 0} \dfrac{2hxy^3+h^2y^3}{h} \\ &=\lim_{h\rightarrow 0} \left(2xy^3+hy^3\right)=2xy^3 \end{aligned}\]
dm,jb
We check by differentiating \(f\) with respect to \(x\) holding \(y\) constant: \(f_x=2xy^3\)
-
Find the value of \(\displaystyle \lim_{h\rightarrow 0} \dfrac{\ln\left(\dfrac{y}{x+h}\right)-\ln\left(\dfrac{y}{x}\right)}{h}\).
Compare the limit to one of: \[\begin{aligned} f_x(x,y)&=\lim_{h\rightarrow 0} \dfrac{f(x+h,y)-f(x,y)}{h} \\ f_y(x,y)&=\lim_{h\rightarrow 0} \dfrac{f(x,y+h)-f(x,y)}{h} \end{aligned}\] Use the second term in the numerator to identify \(f(x,y)\). Then look at the first term in the numerator to see if it is and \(x\) or \(y\) derivative. Then compute that partial derivative.
\(\displaystyle \lim_{h\rightarrow 0} \dfrac{\ln\left(\dfrac{y}{x+h}\right)-\ln\left(\dfrac{y}{x}\right)}{h} =-\,\dfrac{1}{x}\)
We compare the limit to the general partial derivatives: \[\begin{aligned} f_x(x,y)&=\lim_{h\rightarrow 0} \dfrac{f(x+h,y)-f(x,y)}{h} \\ f_y(x,y)&=\lim_{h\rightarrow 0} \dfrac{f(x,y+h)-f(x,y)}{h} \end{aligned}\] We see that \(f(x,y)=\ln\left(\dfrac{y}{x}\right)\). Then looking at the first term in the numerator we see: \[ \ln\left(\dfrac{y}{x+h}\right)=f(x+h,y) \] So this limit must be the \(x\)-partial derivative of \(\ln\left(\dfrac{y}{x}\right)\): \[\begin{aligned} \lim_{h\rightarrow 0} &\dfrac{\ln\left(\dfrac{y}{x+h}\right)-\ln\left(\dfrac{y}{x}\right)}{h} =\dfrac{\partial}{\partial x} \ln\left(\dfrac{y}{x}\right) \\ &= \dfrac{\partial}{\partial x} [\ln(y)-\ln(x)] = -\,\dfrac{1}{x} \end{aligned}\]
gg
This limit can also be computed using a log identity to reduce it to an ordinary derivative: \[\begin{aligned} \lim_{h\rightarrow 0} &\dfrac{\ln\left(\dfrac{y}{x+h}\right)-\ln\left(\dfrac{y}{x}\right)}{h} \\ &= \lim_{h\rightarrow 0} \dfrac{\ln(y)- \ln(x+h) - \ln(y) + \ln(x)}{h}\\ &=-\,\lim_{h\rightarrow 0} \dfrac{\ln(x+h)- \ln(x)}{h} \\ &=-\,\dfrac{d}{dx}(\ln x) =-\,\dfrac{1}{x} \end{aligned}\]
-
Find the value of \(\displaystyle \lim_{h\rightarrow 0} \dfrac{\sin(xy^2+2xyh+xh^2)-\sin(xy^2)}{h}\).
Compare the limit to the general partial derivatives: \[\begin{aligned} f_x(x,y)&=\lim_{h\rightarrow 0} \dfrac{f(x+h,y)-f(x,y)}{h} \\ f_y(x,y)&=\lim_{h\rightarrow 0} \dfrac{f(x,y+h)-f(x,y)}{h} \end{aligned}\] Identify \(f(x,y)\) and then either \(f(x+h,y)\) or \(f(x,y+h)\).
\(\displaystyle \lim_{h\rightarrow 0} \dfrac{\sin(xy^2+2xyh+xh^2)-\sin(xy^2)}{h} =2xy\cos(xy^2)\)
\[\begin{aligned} \lim_{h\rightarrow 0} &\dfrac{\sin(xy^2+2xyh+xh^2)-\sin(xy^2)}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{\sin(x(y^2+2yh+h^2))-\sin(xy^2)}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{\sin(x(y+h)^2)-\sin(xy^2)}{h} \end{aligned}\] According to the algebraic definition of partial derivatives, this is equal to the \(y\)-partial derivative of \(\sin(xy^2)\): \[ =\dfrac{\partial}{\partial y}\sin(xy^2) =2xy\cos(xy^2) \]
dm,jb
-
For the graph of the function \(f=x^2y+\dfrac{x}{y}\), compute
-
the slope of the \(x\)-trace at the point \((2,1)\).
\(f_x(2,1)=5\)
First, we find the partial derivative with respect to \(x\): \[ f_x=2xy+\dfrac{1}{y} \]
Then we plug in the point \((2,1)\): \[f_x(2,1)=4+\dfrac{1}{1}=5\]
dm,jb
-
the tangent line to the \(x\)-trace at the point \((2,1)\).
\(z=5x-4\)
We plug the point \((a,b)=(2,1)\) into the function: \[ f(2,1)=2^2 1+\dfrac{2}{1}=6 \] Using this and the \(x\)-slope, \(f_x(2,1)=5\), we find the tangent line: \[\begin{aligned} z&=f(a,b)+f_x(a,b)(x-a) \\ z&=f(2,1)+f_x(2,1)(x-2) \\ &=6+5(x-2) \\ &=5x-4 \end{aligned}\]
dm,jb
-
the slope of the \(y\)-trace at the point \((2,1)\).
\(f_y(2,1)=2\)
First, we find the partial derivative with respect to \(y\): \[ f_y=x^2-\,\dfrac{x}{y^2} \] Then we plug in the point \((2,1)\): \[ f_y(2,1)=4-\,\dfrac{2}{1}=2 \]
dm,jb
-
the tangent line to the \(y\)-trace at the point \((2,1)\).
\(z=2y+4\)
We plug the point \((a,b)=(2,1)\) into the function: \[ f(2,1)=2^2 1+\dfrac{2}{1}=6 \] Using this and the \(y\)-slope, \(f_y(2,1)=2\), we find the tangent line: \[\begin{aligned} z&=f(a,b)+f_y(a,b)(y-b) \\ z&=f(2,1)+f_y(2,1)(y-1) \\ &=6+2(y-1) \\ &=2y+4 \end{aligned}\]
dm,jb
-
-
For the graph of the function \(g=e^{xy}+xy\), find:
-
the slope of the \(x\)-trace at the point \((3,4)\).
\(g_x(3,4)=4e^{12}+4\)
First, we find the partial derivative with respect to \(x\): \[ g_x(x,y)=ye^{xy}+y \] Then we plug in the point \((3,4)\): \[g_x(3,4)=4e^{12}+4\]
gg
-
the tangent line to the \(x\)-trace at the point \((3,4)\).
\(z=4(e^{12}+1)x - 11e^{12}\)
We plug the point \((a,b)=(3,4)\) into the function: \[ g(3,4)=e^{12}+12 \] Using this and the \(x\)-slope, \(g_x(3,4)=4e^{12}+4\), we find the tangent line: \[\begin{aligned} z&=g(a,b)+g_x(a,b)(x-a) \\ z&=g(3,4)+g_x(3,4)(x-3) \\ &=e^{12}+12+\left(4e^{12}+4\right)(x-3) \\ &=4(e^{12}+1)x - 11e^{12} \end{aligned}\]
gg
-
the slope of the \(y\)-trace at the point \((3,4)\).
\(g_y(3,4)=3e^{12}+ 3\)
First, we find the partial derivative with respect to \(y\): \[ g_y(x,y)=xe^{xy}+x \] Then we plug in the point \((3,4)\): \[ g_y(3,4)=3e^{12}+ 3 \]
gg
-
the tangent line to the \(y\)-trace at the point \((3,4)\).
\(z=3(e^{12}+ 1)y - 11e^{12}\)
We plug the point \((a,b)=(3,4)\) into the function: \[ g(3,4)=e^{12}+12 \] Using this and the \(y\)-slope, \(g_y(3,4)=3e^{12}+ 3\), we find the tangent line: \[\begin{aligned} z&=g(a,b)+g_y(a,b)(y-b) \\ z&=g(3,4)+g_y(3,4)(y-4) \\ &=e^{12}+12 +\left(3e^{12}+ 3\right)(y-4) \\ &=3(e^{12}+ 1)y - 11e^{12} \end{aligned}\]
gg
-
-
For the graph of the function \(f=x^2y+\dfrac{x}{y}\), discussed in a previous exercise, find the equation of the plane tangent at \((2,1)\). Then, find the \(z\)-intercept of the plane.
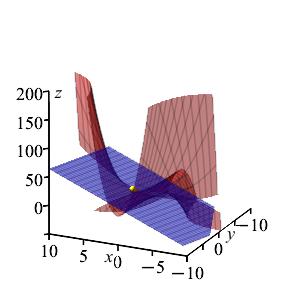
Evaluate the function and its partial derivatives at \((x,y)=(2,1)\). Then use the formula: \[ z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b) \]
\(z=5x+2y-6\)
The \(z\)-intercept is \(-6\).In a previous exercise, we found \[\begin{aligned} f(2,1)&=6 \\ f_x(2,1)&=5 \\ f_y(2,1)&=2 \\ \end{aligned}\] We plug these into the formula: \[\begin{aligned} z&=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b) \\ &=f(2,1)+f_x(2,1)(x-2)+f_y(2,1)(y-1) \\ &=6+5(x-2)+2(y-1) \\ &=5x+2y-6 \end{aligned}\] The \(z\)-intercept is \(-6\).
dm,jb
We have found the tangent plane at \((x,y)=(2,1)\) is: \(z=5x+2y-6\).
Plugging in \(y=1\), the tangent line to the \(x\)-trace is: \(z=5x-4\).
Plugging in \(x=2\), the tangent line to the \(y\)-trace is: \(z=2y+4\).
These agree with the previous exercise.For the graph of the function \(g=e^{xy}+xy\), discussed in a previous exercise, find the equation of the plane tangent at \((3,4)\). Then, find the \(z\)-intercept of the plane.
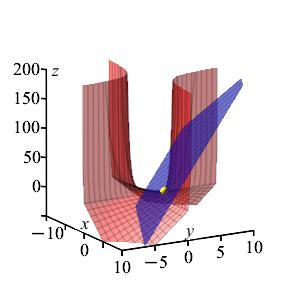
\(z=4(e^{12}+1)x+3(e^{12}+1)y - 23e^{12} - 12\)
The \(z\)-intercept is \(- 23e^{12} - 12\).In a previous exercise, we found \[\begin{aligned} f(3,4)&= e^{12}+ 12 \\ f_x(3,4)&= 4e^{12}+ 4 \\ f_y(3,4)&= 3e^{12}+ 3 \\ \end{aligned}\] We plug these into the formula: \[\begin{aligned} z&=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b) \\ &=f(3,4)+f_x(3,4)(x-3)+f_y(3,4)(y-4) \\ &=e^{12}+12+\left(4e^{12}+4\right)(x-3)+\left(3e^{12}+ 3\right)(y-4) \\ &=4(e^{12}+1)x+3(e^{12}+1)y - 23e^{12} - 12 \end{aligned}\] The \(z\)-intercept is \(- 23e^{12} - 12\).
gg
We have found the tangent plane at \((x,y)=(3,4)\) is: \(z=4(e^{12}+1)x+3(e^{12}+1)y - 23e^{12} - 12\).
Plugging in \(y=4\), the tangent line to the \(x\)-trace is: \(z=4(e^{12}+1)x -11e^{12}\).
Plugging in \(x=3\), the tangent line to the \(y\)-trace is: \(z=3(e^{12}+1)y -11e^{12}\).
These agree with the previous exercise.Find the equation of the plane tangent to \(z=x^2+y^3\) at the point \((x,y)=(2,1)\). Then find its \(z\)-intercept.
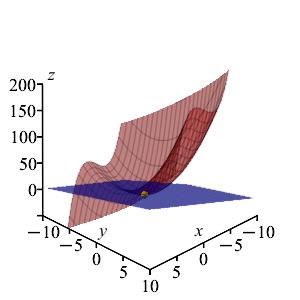
Find the values of the function and its partial derivatives at \((2,1)\).
Then plug into the formula for the tangent plane: \[ z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b) \] Read off the \(z\)-intercept \(c\) from the equation \(z=mx+ny+c\).\(z=4x+3y-6\).
\(c=-6\).We identify \(f(x,y)=x^2+y^3\), \(a=2\) and \(b=1\). For the tangent plane equation, we need \(f(2,1)\), \(f_x(2,1)\), and \(f_y(2,1)\). It is good to make a table: \[\begin{aligned} &f=x^2+y^3 \qquad &f(2,1)=5 \\ &f_x=2x \qquad &f_x(2,1)=4 \\ &f_y=3y^2 \qquad &f_y(2,1)=3 \end{aligned}\] So the equation of the tangent plane is: \[\begin{aligned} z&=f(2,1)+f_x(2,1)(x-2)+f_y(2,1)(y-1) \\ &=5+4(x-2)+3(y-1) \\ &=4x+3y-6 \end{aligned}\] We identify the \(z\)-intercept as \(c=-6\).
dm,jb
Find the equation of the plane tangent to \(z=x^2+y^2\) at the point \((3,1)\). Then, find the \(z\)-intercept of the plane.
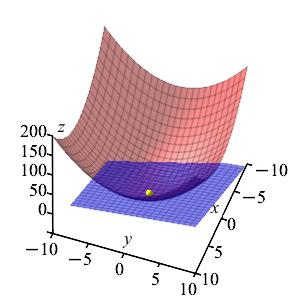
\(z=6x+2y-10\).
\(c=-10\).First, we find the value of the function, \(f(x,y)=x^2+y^2\), at the point \((3,1)\): \[ f(3,1)=3^2+1^2=10 \] Next, we calculate \(f_x\) and \(f_y\) at the point \((3,1)\): \[\begin{aligned} f_x&=2x \qquad f_x(3,1)=6 \\ f_y&=2y \qquad f_y(3,1)=2 \end{aligned}\] Finally, we plug these values into the equation for the tangent plane: \[\begin{aligned} z&=f(3,1)+f_x(3,1)(x-3)+f_y(3,1)(y-1) \\ &=10+6(x-3)+2(y-1)\\ &=6x+2y-10 \end{aligned}\] So the \(z\)-intercept is \(c=-10\).
dm,jb
Find the equation of the plane tangent to \(z=x^2y+xy^2\) at \((x,y)=(2,1)\). Then find the \(z\)-intercept.
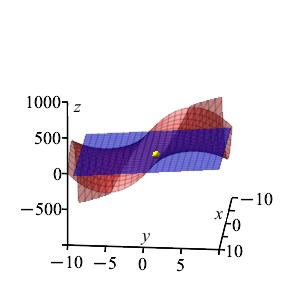
\(z=5x+8y-12\).
\(c=-12\).We identify \(a=2\) and \(b=1\): \[\begin{aligned} &f=x^2y+xy^2 \qquad &f(2,1)=6 \\ &f_x=2xy+y^2 \qquad &f_x(2,1)=5 \\ &f_y=x^2+2xy \qquad &f_y(2,1)=8 \end{aligned}\] We now plug this information into the equation for a tangent plane: \[\begin{aligned} z&=f(2,1)+f_x(2,1)(x-2)+f_y(2,1)(y-1) \\ &=6+5(x-2)+8(y-1) \\ &=5x+8y-12 \end{aligned}\] We identify the \(z\)-intercept as \(c=-12\).
dm,jb,tc
Find the equation of the tangent plane at the point \((2,4)\) for the function \(z=x^2y-x(y+3)+4\). Then, find the \(z\)-intercept of the plane.
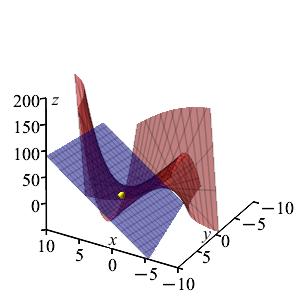
\(z=9x+2y-20\)
\(c=-20\).We evaluate the function and its derivatives at the point \((2,4)\): \[\begin{aligned} f(x,y)&=x^2y-x(y+3)+4 &f(2,4)&=2^2(4)-2(4+3)+4=6 \\ f_x&=2xy-y-3 &f_x(2,4)&=2(2)(4)-4-3=9 \\ f_y&=x^2-x &f_y(2,4)&=2^2-2=2 \end{aligned}\] Finally, we plug these values into the tangent plane: \[\begin{aligned} z&=f(2,4)+f_x(2,4)(x-2)+f_y(2,4)(y-4) \\ &=6+9(x-2)+2(y-4) \\ &=9x+2y-20 \end{aligned}\] So the \(z\)-interept is \(c=-20\).
dm,jb
Compute the tangent plane to \(z=\sin x\cos y\) at \((x,y)=\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right)\). Then find the \(z\)-intercept.
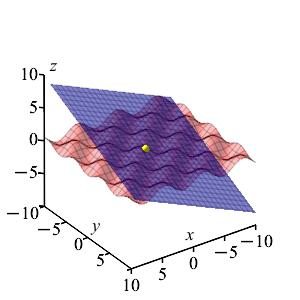
What are the values of \(\sin\) and \(\cos\) at \(\dfrac{\pi}{3}\) and \(\dfrac{\pi}{6}\)?
\(z=\dfrac{\sqrt{3}}{4}x-\,\dfrac{\sqrt{3}}{4}y +\dfrac{3}{4}-\,\dfrac{\sqrt{3}\,\pi}{24}\)
\(c=\dfrac{3}{4}-\,\dfrac{\sqrt{3}\,\pi}{24}\).The function, its partial derivatives, and their values at \((x,y)=\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right)\) are: \[\begin{aligned} f&=\sin x\cos y \ & f\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right) &=\sin\dfrac{\pi}{3}\cos\dfrac{\pi}{6} =\dfrac{\sqrt{3}}{2}\dfrac{\sqrt{3}}{2} =\dfrac{3}{4} \\ f_x&=\cos x\cos y \ & f_x\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right) &=\cos\dfrac{\pi}{3}\cos\dfrac{\pi}{6} =\dfrac{1}{2}\dfrac{\sqrt{3}}{2} =\dfrac{\sqrt{3}}{4} \\ f_y&=-\sin x\sin y \ & f_y\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right) &=-\sin\dfrac{\pi}{3}\sin\dfrac{\pi}{6} =-\,\dfrac{\sqrt{3}}{2}\dfrac{1}{2} =-\,\dfrac{\sqrt{3}}{4} \end{aligned}\] So the equation of the tangent plane is: \[\begin{aligned} z&=f\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right) +f_x\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right)\left(x-\,\dfrac{\pi}{3}\right) +f_y\left(\dfrac{\pi}{3},\dfrac{\pi}{6}\right)\left(y-\,\dfrac{\pi}{6}\right) \\ &=\dfrac{3}{4} +\dfrac{\sqrt{3}}{4}\left(x-\,\dfrac{\pi}{3}\right) -\,\dfrac{\sqrt{3}}{4}\left(y-\,\dfrac{\pi}{6}\right) \\ &=\dfrac{\sqrt{3}}{4}x-\,\dfrac{\sqrt{3}}{4}y +\dfrac{3}{4} -\,\dfrac{\sqrt{3}\,\pi}{12} +\dfrac{\sqrt{3}\,\pi}{24} \\ &=\dfrac{\sqrt{3}}{4}x-\,\dfrac{\sqrt{3}}{4}y +\dfrac{3}{4}-\,\dfrac{\sqrt{3}\,\pi}{24} \end{aligned}\] We identify the \(z\)-intercept as \(c=\dfrac{3}{4}-\dfrac{\sqrt{3}\,\pi}{24}\).
dm,jb
Find \(f_x\), \(f_y\) \(f_z\) for the function \(f=x\sin(yz)\).
\(f_x=\sin(yz)\)
\(f_y=xz\cos(yz)\)
\(f_z=xy\cos(yz)\)We differentiate \(f=x\sin(yz)\) with respect to \(x\), \(y\), and \(z\). We get: \[\begin{aligned} f_x&=\sin(yz) \\ f_y&=xz\cos(yz) \\ f_z&=xy\cos(yz) \end{aligned}\]
dm,jb
Find the equation of the tangent hyperplane to the function \(w=f(x,y,z)=x^3y^2z\) at the point \((1,2,3)\).
\(w=36x+12y+4z-60\)
We find the values of the function and its partial derivatives at the point \((1,2,3)\): \[\begin{aligned} f&=x^3y^2z &f(1,2,3)&=12 \\ f_x&=3x^2y^2z &f_x(1,2,3)&=36 \\ f_y&=2x^3yz &f_y(1,2,3)&=12 \\ f_z&=x^3y^2 &f_z(1,2,3)&=4 \end{aligned}\] Then, we plug these into the tangent hyperplane: \[\begin{aligned} w&=f_{\tan}(x,y,z) \\ &=f(1,2,3)+f_x(1,2,3)(x-1)\\ &\qquad +f_y(1,2,3)(y-2)+f_z(1,2,3)(z-3) \\ &=12+36(x-1)+12(y-2)+4(z-3) \\ &=36x+12y+4z-60 \end{aligned}\]
dm,jb
According to the ideal gas law, \(P=\dfrac{nRT}{V}\) where \(R\) is a constant. Find the partial derivatives of the pressure, \(P\), with respect to the volume, \(V\), the mole number, \(n\) and the temperature, \(T\).
\(\begin{aligned} \dfrac{\partial P}{\partial V} &=-\,\dfrac{nRT}{V^2} \\ \dfrac{\partial P}{\partial n} &=\dfrac{RT}{V} \\ \dfrac{\partial P}{\partial T} &=\dfrac{nR}{V} \end{aligned}\)
As we differentiate with respect to each variable, we keep the other variables constants: \[\begin{aligned} \dfrac{\partial P}{\partial V} &=\dfrac{\partial}{\partial V} \dfrac{nRT}{V} = -\,\dfrac{nRT}{V^2} \\[5pt] \dfrac{\partial P}{\partial n} &=\dfrac{\partial}{\partial n} \dfrac{nRT}{V} = \dfrac{RT}{V} \\[5pt] \dfrac{\partial P}{\partial T} &=\dfrac{\partial}{\partial T} \dfrac{nRT}{V} = \dfrac{nR}{V} \end{aligned}\]
gg
The intensity of microwaves in a microwave oven at the point, \((x,y,z)\), is modeled by the function \(I(x,y,z)= e^{-(x^2+y^2+z^2)} \cos^2 4y \cos^2 4x\). A grain of rice is located at \(\left(\dfrac{\pi}{16},\dfrac{\pi}{16}, 0\right)\). Find the rate of change of the intensity in the \(x\), \(y\), and \(z\) directions at the grain of rice.
The rates of change are the partial derivatives \(\partial_x I\), \(\partial_y I\), and \(\partial_z I\). Use the product rule and remember the other variables are constants. Note some variables occur symetrically.
\(\begin{aligned} \partial_x I&=-2e^{-\pi^2/128}\left(1+ \dfrac{\pi}{64}\right) \\ \partial_y I&=-2e^{-\pi^2/128}\left(1+ \dfrac{\pi}{64}\right) \\ \partial_z I&= 0 \end{aligned}\)
First, lets find \(\partial_x I\). We notice \(\cos^2 4y\) is a constant. Then we use the Product Rule: \[\begin{aligned} \partial_x I &=\dfrac{\partial}{\partial x}\Big[e^{-(x^2+y^2+z^2)} \cos^2 4y \cos^2 4x\Big]\\ &=\cos^2 4y \Big[e^{-(x^2+y^2+z^2)}2\cos 4x(-\sin 4x)(4)\\ &\qquad\qquad\quad+ e^{-(x^2+y^2+z^2)}(-2x)\cos^2 4x \Big] \\ &=-2e^{-(x^2+y^2+z^2)}\cos^2 4y\cos 4x\big(4\sin 4x+ x\cos 4x\big) \end{aligned}\] We observe that the formula for \(I\) is unchanged if we interchange \(x\) and \(y\). So \(\partial_y I\) is the same as \(\partial_x I\), but with \(x\) and \(y\) interchanged: \[ \partial_y I=-2e^{-(x^2+y^2+z^2)}\cos^2 4x\cos 4y\big(4\sin 4y+ y\cos 4y\big) \] Next, we find \(\partial_z I\). This time \(\cos^2 4y\cos^2 4x\) is a constant. \[\begin{aligned} \partial_z I &= \dfrac{\partial}{\partial z}\Big[e^{-(x^2+y^2+z^2)} \cos^2 4y \cos^2 4x\Big]\\ &= \cos^2 4x\cos^2 4y \left[e^{-(x^2+y^2+z^2)}(-2z)\right] \\ &= -2ze^{-(x^2+y^2+z^2)} \cos^2 4y \cos^2 4x \end{aligned}\] Finally, we evaluate at the position of the rice \((x,y,z)=\left(\dfrac{\pi}{16},\dfrac{\pi}{16}, 0\right)\): \[\begin{aligned} \partial_x I &=-2e^{-(\pi^2/16^2+\pi^2/16^2)}\cos^2 \dfrac{\pi}{4}\cos \dfrac{\pi}{4} \left(4\sin\dfrac{\pi}{4}+ \dfrac{\pi}{16}\cos\dfrac{\pi}{4}\right)\\ &=-2e^{-\pi^2/128}\left(\dfrac{1}{\sqrt{2}}\right)^4 \left(4+ \dfrac{\pi}{16}\right)\\ &=-2e^{-\pi^2/128}\left(1+ \dfrac{\pi}{64}\right)\\[10pt] \partial_y I &=\partial_x I = -2e^{-\pi^2/128}\left(1+ \dfrac{\pi}{64}\right)\\ \partial_z I &= -2(0)e^{-(\pi^2/16+\pi^2/16)} \cos^2 \dfrac{\pi}{4} \cos^2 \dfrac{\pi}{4} = 0 \end{aligned}\]
gg
Review Exercises
Find the slopes of the \(x\)-trace and the \(y\)-trace of the function \(f(x,y)=x^3y^4\) at the point \((3,1)\).
The slope of the \(x\)-trace is \(27\).
The slope of the \(y\)-trace is \(108\).We find the partial derivatives with respect to \(x\) and \(y\) and evaluate at \((3,1)\): \[\begin{aligned} f_x&=3x^2y^4 \qquad &f_x(3,1)&=3(3^2)(1^4)=27 \\ f_y&=4x^3y^3 \qquad &f_y(3,1)&=4(3^3)(1^3)=108 \end{aligned}\] So the slope of the \(x\)-trace is \(27\) and slope of the \(y\)-trace is \(108\).
dm,jb
Find the equation of the tangent hyperplane to the function \(w=f(x,y,z)=x^2yz^3\) at the point \((1,3,3)\).
The tangent hyperplane is: \(w=162x+27y+81z-405\)
We find the values of the function and its partial derivatives at the point \((1,3,3)\): \[\begin{aligned} f&=x^2yz^3 &f(1,3,3)&=81 \\ f_x&=2xyz^3 \qquad &f_x(1,3,3)&=162 \\ f_y&=x^2z^3 \qquad &f_y(1,3,3)&=27 \\ f_z&=3x^2yz^2 \qquad &f_z(1,3,3)&=81 \end{aligned}\] Then, we substitute these into the equation of the tangent hyperplane: \[\begin{aligned} w&=f_{\tan}(x,y,z) \\ &=f(1,3,3)+f_x(1,3,3)(x-a)+f_y(1,3,3)(y-b)+f_z(1,3,3)(z-c) \\ &=81+162(x-1)+27(y-3)+81(z-3) \\ &=162x+27y+81z+81-162-81-243 \\ &=162x+27y+81z-405 \\ \end{aligned}\]
dm,jb
×Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum
For each function find the indicated partial derivatives.