15. Polar Coordinates

Polar Curve as a Parametric Curve

Notice that any polar curve \(r=f(\theta)\) can be regarded as a parametric curve with parameter \(\theta\) and coordinate functions: \[ x(\theta)=r\cos\theta=f(\theta)\cos\theta \qquad \qquad y(\theta)=r\sin\theta=f(\theta)\sin\theta \] Normally, we remove the reference to \(f\), writing \(r=r(\theta)\) and: \[ x(\theta)=r(\theta)\cos\theta \qquad \qquad y(\theta)=r(\theta)\sin\theta \] Then the position vector of the curve is \[ \vec{r}(\theta)=(x(\theta),y(\theta)) =(r(\theta)\cos\theta,r(\theta)\sin\theta) \] Note on \(r(\theta)\) vs. \(\vec r(\theta)\)

We will use this formulation in two of our applications of polar curves: slope and arclength.

c. Slope of a Polar Graph

Recall that the slope of a parametric curve \(\vec{r}(\theta)=(x(\theta),y(\theta))\) is: \[ \dfrac{dy}{dx} =\dfrac {\;\dfrac{dy}{d\theta}\;} {\;\dfrac{dx}{d\theta}\;} \] In fact, applying the product rule to a polar curve gives: \[\begin{aligned} \dfrac{dx}{d\theta} &=\dfrac{dr}{d\theta}\cos\theta-r(\theta)\sin\theta\\ \dfrac{dy}{d\theta} &=\dfrac{dr}{d\theta}\sin\theta+r(\theta)\cos\theta \end{aligned}\] Consequently:

The slope of a polar curve \(r=r(\theta)\) is \[ \dfrac{dy}{dx} =\dfrac {\;\dfrac{dr}{d\theta}\sin\theta+r(\theta)\cos\theta\;} {\;\dfrac{dr}{d\theta}\cos\theta-r(\theta)\sin\theta\;} \] provided the denominator is non-zero.

Caution: Remember, \(\dfrac{dy}{d\theta}\) is in the numerator and \(\dfrac{dx}{d\theta}\) is in the denominator. It is easy to get these backwards.

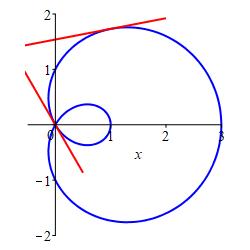
Since \(\dfrac{dr}{d\theta}=-2\sin\theta\), the slope is \[\begin{aligned} \dfrac{dy}{dx} &=\dfrac{-2\sin\theta\sin\theta+(1+2\cos\theta)\cos\theta} {-2\sin\theta\cos\theta-(1+2\cos\theta)\sin\theta} \\ \end{aligned}\]

1. At \(\theta=\dfrac{\pi}{3}=60^\circ\), \(\sin\theta=\dfrac{\sqrt{3}}{2}\) and \(\cos\theta=\dfrac{1}{2}\). So: \[\begin{aligned} \left.\dfrac{dy}{dx}\right|_{\theta=\pi/3} &=\dfrac{\;-2\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right) +\left(1+2\left(\frac{1}{2}\right)\right)\left(\frac{1}{2}\right)\;} {\;-2\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right) -\left(1+2\left(\frac{1}{2}\right)\right)\left(\frac{\sqrt{3}}{2}\right)\;} \\ &=\dfrac{\;-\,\frac{3}{2}+1\;}{\;-\,\frac{\sqrt{3}}{2}-\sqrt{3}\;} =\dfrac{-\,\frac{1}{2}}{-\,\frac{3\sqrt{3}}{2}}=\dfrac{1}{3\sqrt{3}} \end{aligned}\]
2. At \(\theta=\dfrac{2\pi}{3}=120^\circ\), \(\sin\theta=\dfrac{\sqrt{3}}{2}\) and \(\cos\theta=\dfrac{-1}{2}\). So: \[\begin{aligned} \left.\dfrac{dy}{dx}\right|_{\theta=2\pi/3} &=\dfrac{\;-2\left(\frac{\sqrt{3}}{2}\;\right)\left(\frac{\sqrt{3}}{2}\right) +\left(1+2\left(-\,\frac{1}{2}\right)\right)\left(-\,\frac{1}{2}\right)\;} {\;-2\left(\frac{\sqrt{3}}{2}\right)\left(-\,\frac{1}{2}\right) -\left(1+2\left(-\,\frac{1}{2}\right)\right)\left(\frac{\sqrt{3}}{2}\right)\;} \\ &=\dfrac{\;-\frac{3}{2}+0\;}{\;\frac{\sqrt{3}}{2}-0\;} =\dfrac{-3}{\sqrt{3}}=-\sqrt{3} \end{aligned}\]

In this example, notice that \(\tan\dfrac{2\pi}{3}=-\sqrt{3}\) which is the slope at \(\theta=\dfrac{2\pi}{3}\). This is no coincidence. Look at the figure. Notice that the curve comes into the origin tangent to the line \(\theta=\dfrac{2\pi}{3}\) and the slope of that line is \(\tan\dfrac{2\pi}{3}\).

If \(\theta=\theta_o\) is a point where the polar curve \(r=r(\theta)\) passes through the origin, i.e. \(r(\theta_o)=0\), then the slope at \(\theta=\theta_o\) is: \[ \left.\dfrac{dy}{dx}\right|_{\theta=\theta_o}=\tan\theta_o \] Proof