7. Chain Rule & Implicit Differentiation
Exercises
-
Consider the functions \(f(x)=3x\) and \(g(x)=2x\). Compute \(g(4)\) and \(f(g(4))\).
\(g(4)=8\)
\(f(g(4))=24\)We replace the \(x\) in \(g(x)=2x\) by \(4\): \[ g(4)=2\cdot4=8 \] Next we replace the \(x\) in \(f(x)=3x\) by \(g(4)=8\): \[ f(g(4))=3\cdot8=24 \]
ad
-
Consider the functions \(f(x)=3x^2+2\) and \(g(x)=4x+1\). Compute \(g(2)\) and \(f(g(2))\).
\(g(2)=9\)
\(f(g(2))=245\)We replace the \(x\) in \(g(x)=4x+1\) by \(2\): \[ g(2)=4\cdot2+1=8+1=9 \] Next we replace the \(x\) in \(f(x)=3x^2+2\) by \(g(2)=9\): \[ f(g(2))=3\cdot9^2+2=3\cdot81+2=243+2=245 \]
ad
-
Consider the functions \(f(x)=3\cos(\pi x)\) and \(g(x)=\sin(\pi x)\). Compute \(f\left(\dfrac{1}{3}\right)\) and \(g\left(f\left(\dfrac{1}{3}\right)\right)\).
\(f\left(\dfrac{1}{3}\right)=\dfrac{3}{2}\)
\(g\left(f\left(\dfrac{1}{3}\right)\right)=-1\)We replace the \(x\) in \(f(x)=3\cos(\pi x)\) by \(\dfrac{1}{3}\): \[ f\left(\dfrac{1}{3}\right)=3\cos\left(\dfrac{\pi}{3}\right) =3\cdot\dfrac{1}{2}=\dfrac{3}{2} \] Next we replace the \(x\) in \(g(x)=\sin(\pi x)\) by \(f\left(\dfrac{1}{3}\right)=\dfrac{3}{2}\): \[ g\left(f\left(\dfrac{1}{3}\right)\right)=\sin\left(\dfrac{3\pi}{2}\right) =-1 \]
ad
-
Consider the functions \(f(x)=3x^2+5\) and \(g(x)=4x^2+1\).
-
Compute \(g(1)\) and \(f(g(1))\).
\(g(1)=5\)
\(f(g(1))=80\)We replace the \(x\) in \(g(x)=4x^2+1\) by \(1\): \[ g(1)=4\cdot1^2+1=4+1=5 \] Next we replace the \(x\) in \(f(x)=3x^2+5\) by \(g(1)=5\): \[ f(g(1))=3\cdot5^2+5=3\cdot25+5=75+5=80 \]
ad
-
Compute \(f(1)\) and \(g(f(1))\).
\(f(1)=8\)
\(g(f(1))=257\)We replace the \(x\) in \(f(x)=3x^2+5\) by \(1\): \[ f(1)=3\cdot1^2+5=3+5=8 \] Next we replace the \(x\) in \(g(x)=4x^2+1\) by \(f(1)=8\): \[ g(f(1))=4\cdot8^2+1=4\cdot64+1=256+1=257 \]
ad
Notice that \(g(f(1))\) is not the same as \(f(g(1))\).
-
Compute \(f(g(x))\).
\(f(g(x))=48x^4+24x^2+8\)
We replace the \(x\) in \(f(x)=3x^2+5\) by \(g(x)=4x^2+1\): \[\begin{aligned} f(g(x))&=f(4x^2+1) \\ &=3(4x^2+1)^2+5 \\ &=3(16x^4+8x^2+1)+5 \\ &=48x^4+24x^2+3+5 \\ &=48x^4+24x^2+8 \end{aligned}\]
ad
Since \(f(g(x))=48x^4+24x^2+8\), we compute: \[\begin{aligned} f(g(1))&=48\cdot1^4+24\cdot1^2+8 \\ &=48+24+8=80 \end{aligned}\] which agrees with the answer in part (a).
-
Compute \(g(f(x))\).
\(g(f(x))=36x^4+120x^2+101\)
We replace the \(x\) in \(g(x)=4x^2+1\) by \(f(x)=3x^2+5\): \[\begin{aligned} g(f(x))&=g(3x^2+5) \\ &=4(3x^2+5)^2+1 \\ &=4(9x^4+30x^2+25)+1 \\ &=36x^4+120x^2+100+1 \\ &=36x^4+120x^2+101 \end{aligned}\]
ad
Since \(g(f(x))=36x^4+120x^2+101\), we compute: \[\begin{aligned} g(f(1))&=36\cdot1^4+120\cdot1^2+101 \\ &=36+120+101=257 \end{aligned}\] which agreees with the answer in part (b).
Notice that \(g(f(x))\) is not the same as \(f(g(x))\).
-
-
Consider the functions \(f(x)=x^2+2x\) and \(g(x)=x^3-4x\).
-
Compute \(g(3)\) and \(f(g(3))\).
\(g(3)=15\)
\(f(g(3))=255\)We replace the \(x\) in \(g(x)=x^3-4x\) by \(3\): \[ g(3)=3^3-4\cdot3=27-12=15 \] Next we replace the \(x\) in \(f(x)=x^2+2x\) by \(g(3)=15\): \[ f(g(3))=(15)^2+2(15)=225+30=255 \]
ad
-
Compute \(f(3)\) and \(g(f(3))\).
\(f(3)=15\)
\(g(f(3))=3315\)We replace the \(x\) in \(f(x)=x^2+2x\) by \(3\): \[ f(3)=3^2+2\cdot3=9+6=15 \] Next we replace the \(x\) in \(g(x)=x^3-4x\) by \(f(3)=15\): \[ g(f(3))=(15)^3-4(15)=3375-60=3315 \]
ad
Notice that \(g(f(3))\) is not the same as \(f(g(3))\).
-
Compute \(f(g(x))\).
\(f(g(x))=x^6-8x^4+2x^3+16x^2-8x\)
We replace the \(x\) in \(f(x)=x^2+2x\) by \(g(x)=x^3-4x\): \[\begin{aligned} f(g(x))&=f(x^3-4x) \\ &=(x^3-4x)^2+2(x^3-4x) \\ &=x^6-8x^4+16x^2+2x^3-8x \\ &=x^6-8x^4+2x^3+16x^2-8x \end{aligned}\]
ad
If \(f(g(x))=x^6-8x^4+2x^3+16x^2-8x\), then \[\begin{aligned} f(g(3))&=3^6-8\cdot3^4+2\cdot3^3+16\cdot3^2-8\cdot3 \\ &=729-648+54+144-24 =255 \end{aligned}\] which agrees with the answer in part (a).
-
Compute \(g(f(x))\).
\(g(f(x))=x^6+6x^5+12x^4+8x^3-4x^2-8x\)
We replace the \(x\) in \(g(x)=x^3-4x\) by \(f(x)=x^2+2x\): \[\begin{aligned} g(f(x))&=g(x^2+2x) \\ &=(x^2+2x)^3-4(x^2+2x) \\ &=x^6+6x^5+12x^4+8x^3-4x^2-8x \end{aligned}\]
ad
If \(g(f(x))=x^6+6x^5+12x^4+8x^3-4x^2-8x\), then \[\begin{aligned} g(f(3))&=3^6+6\cdot3^5+12\cdot3^4+8\cdot3^3-4\cdot3^2-8\cdot3 \\ &=729+1458+972+216-36-24 =3315 \end{aligned}\] which agreees with the answer in part (b).
Notice that \(g(f(x))\) is not the same as \(f(g(x))\).
-
-
Consider the functions \(f(u)=\cos(\pi u)\) and
\(g(u)=\sin(\pi u)\).
-
Compute \(g\left(\dfrac{1}{6}\right)\) and \(f\left(g\left(\dfrac{1}{6}\right)\right)\).
\(g\left(\dfrac{1}{6}\right)=\dfrac{1}{2}\)
\(f\left(g\left(\dfrac{1}{6}\right)\right)=0\)We replace the \(u\) in \(g(u)=\sin(\pi u)\) by \(\dfrac{1}{6}\): \[ g\left(\dfrac{1}{6}\right)=\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2} \] Next we replace the \(u\) in \(f(u)=\cos(\pi u)\) by \(g\left(\dfrac{1}{6}\right)=\dfrac{1}{2}\): \[ f\left(g\left(\dfrac{1}{6}\right)\right)=\cos\left(\frac{\pi}{2}\right)=0 \]
ad
-
Compute \(f\left(\dfrac{1}{6}\right)\) and \(g\left(f\left(\dfrac{1}{6}\right)\right)\).
\(f\left(\dfrac{1}{6}\right)=\dfrac{\sqrt{3}}{2}\)
\(g\left(f\left(\dfrac{1}{6}\right)\right)=\sin\left({\dfrac{\pi\sqrt{3}}{2}}\right)\)We replace the \(u\) in \(f(u)=\cos(\pi u)\) by \(\dfrac{1}{6}\): \[ f\left(\dfrac{1}{6}\right)=\cos\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2} \] Next we replace the \(u\) in \(g(u)=\sin(\pi u)\) by \(f\left(\dfrac{1}{6}\right)=\dfrac{\sqrt{3}}{2}\): \[ g\left(f\left(\dfrac{1}{6}\right)\right)=\sin\left(\dfrac{\pi\sqrt{3}}{2}\right) \]
ad
Notice that \(g\left(f\left(\dfrac{1}{6}\right)\right)\) is not the same as \(f\left(g\left(\dfrac{1}{6}\right)\right)\).
-
Compute \(f(g(u))\).
\(f(g(u))=\cos(\pi\sin(\pi u))\)
We replace the \(u\) in \(f(u)=\cos(\pi u)\) by \(g(u)=\sin(\pi u)\): \[\begin{aligned} f(g(u))=\cos(\pi\sin(\pi u)) \end{aligned}\]
ad
If \(f(g(u))=\cos(\pi\sin(\pi u))\), then \[\begin{aligned} f\left(g\left(\dfrac{1}{6}\right)\right)&=\cos\left(\pi\sin\left(\dfrac{\pi}{6}\right)\right) \\ &=\cos\left(\dfrac{\pi}{2}\right) \\ &=0\end{aligned}\] which agrees with the answer in part (a).
-
Compute \(g(f(u))\).
\(g(f(u))=\sin(\pi\cos(\pi u))\)
We replace the \(u\) in \(g(u)=\sin(\pi u)\) by \(f(u)=\cos(\pi u)\): \[\begin{aligned} g(f(u))&=\sin(\pi\cos(\pi u)) \end{aligned}\]
ad
If \(g(f(u))=\sin(\pi\cos(\pi u))\), then \[\begin{aligned} g\left(f\left(\dfrac{1}{6}\right)\right)&=\sin\left(\pi\cos\left(\dfrac{\pi}{6}\right)\right) \\ &=\sin\left(\dfrac{\pi\sqrt{3}}{2}\right) \end{aligned}\] which agreees with the answer in part (b).
Notice that \(g(f(x))\) is not the same as \(f(g(x))\).
-
-
Consider the functions \(f(x)\) and \(g(x)\) whose graphs are shown below.
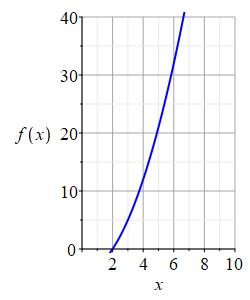
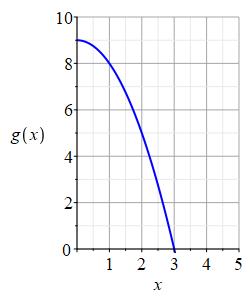
To enlarge the plot, press Ctrl-+. To return, press Ctrl-- or Ctrl-0.
-
Approximate \(g(2)\) and \(f(g(2))\).
\(g(2)=5\)
\(f(g(2))=21\)
Don't feel bad if you are off by a little. Plots can be hard to read.We look at the graph of \(g(x)\) at \(x=2\) and read off \(g(2)=5\).
Next, we look at the graph of \(f(x)\) at \(x=g(2)=5\) and read off \(f(g(2))=f(5)=21\). -
Approximate \(f(2)\) and \(g(f(2))\).
\(f(2)=0\)
\(g(f(2))=9\)We look at the graph of \(f(x)\) at \(x=2\) and read off \(f(2)=0\).
Next, we look at the graph of \(g(x)\) at \(x=f(2)=0\) and read off \(g(f(2))=g(0)=9\).Notice that \(g(f(2))=9\) is not the same as \(f(g(2))=21\).
Consider the functions \(f(x)\) and \(g(x)\) whose graphs are shown below.
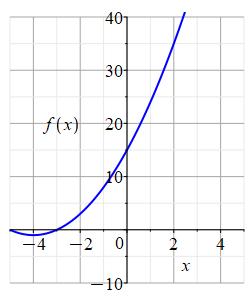
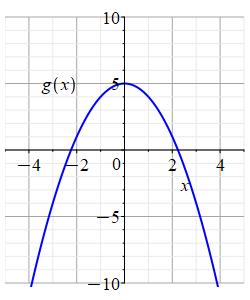
To enlarge the plot, press Ctrl-+. To return, press Ctrl-- or Ctrl-0.
-
Approximate \(g(-2)\) and \(f(g(-2))\).
\(g(-2)=1\)
\(f(g(-2))=24\)
Don't feel bad if you are off by a little. Plots can be hard to read.We look at the graph of \(g(x)\) at \(x=-2\) and read off \(g(-2)=1\).
Next, we look at the graph of \(f(x)\) at \(x=g(-2)=1\) and read off \(f(g(-2))=f(1)=24\). -
Approximate \(f(-2)\) and \(g(f(-2))\).
\(f(-2)=3\)
\(g(f(-2))=-4\)We look at the graph of \(f(x)\) at \(x=-2\) and read off \(f(-2)=3\).
Next, we look at the graph of \(g(x)\) at \(x=f(-2)=3\) and read off \(g(f(-2))=g(3)=-4\).Notice that \(g(f(-2))\) is not the same as \(f(g(-2))\).
Find the derivative of \(y\) with respect to \(t\) for \(y=4x\) and \(x=7t\).
\(\dfrac{dy}{dt}=28\)
The Chain Rule gives \(\dfrac{dy}{dt}=\dfrac{dy}{dx}\dfrac{dx}{dt}\).
First, we find the information we need for the formula: \[ \dfrac{dy}{dx}=4\qquad\dfrac{dx}{dt}=7 \]
We then plug these values into the formula for the Chain Rule: \[\begin{aligned} \dfrac{dy}{dt}&=4\cdot7=28 \end{aligned}\]ad
Since we have complete information, we check by computing the composition and taking its derivative directly: \[\begin{aligned} y(x(t))&=4(7t)=28t \\ \dfrac{dy}{dt}&=28 \end{aligned}\]
Find the derivative of \(y\) with respect to \(t\) for \(y=5x^2+2x+3\) and \(x=3t^2+4\).
\(\dfrac{dy}{dt}=180t^3+252t\)
The Chain Rule gives \(\dfrac{dy}{dt}=\dfrac{dy}{dx}\dfrac{dx}{dt}\).
First, we find the information we need for the formula: \[ \dfrac{dy}{dx}=10x+2\qquad\dfrac{dx}{dt}=6t \] We then plug these values into the formula for the Chain Rule: \[ \dfrac{dy}{dt}=(10x+2)6t \]
Then we remember that the derivative of the outer function needs to be evaluated at the inner function. \[\begin{aligned} \dfrac{dy}{dt}&=(10(3t^2+4)+2)6t=(30t^2+42)6t \\ &=180t^3+252t \end{aligned}\]ad
Since we have complete information, we check by computing the composition and taking its derivative directly: \[\begin{aligned} y(x(t))&=5(3t^2+4)^2+2(3t^2+4)+3 \\ &=5(9t^4+24t^2+16)+6t^2+8+3 \\ &=45t^4+120t^2+80+6t^2+11 \\ &=45t^4+126t^2+91 \\ \dfrac{dy}{dt}&=180t^3+252t \end{aligned}\]
Consider the functions \(f(x)\) and \(g(x)\) whose graphs are shown below. Estimate \((f\circ g)'(2)\).


To enlarge the plot, press Ctrl-+. To return, press Ctrl-- or Ctrl-0.
Approximately, what are \(g(2)\) and \(g'(2)\)? Then what is \(f'(g(2))\)?
\(\displaystyle f'(g(2))\approx-40\)
Looking at the graph of \(g\), we see \(g(2)\approx5\). Drawing a tangent line to \(g\) at \(x=2\), we see \(g'(2)\approx-4\). (The tangent line passes through the points \((1,9)\) and \((3,1)\). Compute the slope.)
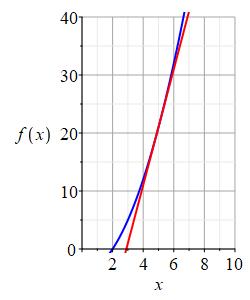
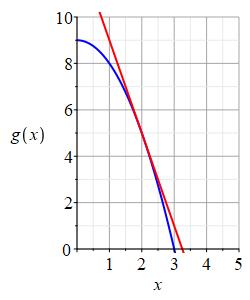
Looking at the graph of \(f\), we draw a tangent line at \(x=g(2)=5\). Its slope is approximately \(f'(g(2))=f'(5)\approx10\). (The tangent line passes through the points \((3,0)\) and \((7,40)\). Compute the slope.) So \[ (f\circ g)'(2)=f'(g(2))g'(2)\approx(10)(-4)=-40 \]
Consider the functions \(f(x)\) and \(g(x)\) whose graphs are shown below. Estimate \((f\circ g)'(-2)\).


To enlarge the plot, press Ctrl-+. To return, press Ctrl-- or Ctrl-0.
Approximately, what are \(g(-2)\) and \(g'(-2)\)? Then what is \(f'(g(-2))\)?
\(\displaystyle (f\circ g)'(-2)\approx40\)
Looking at the graph of \(g\), we see \(g(-2)\approx1\). Drawing a tangent line to \(g\) at \(x=-2\), we see \(g'(-2)\approx4\). (The tangent line passes through the points \((-4,-7)\) and \((0,9)\). Compute the slope.)
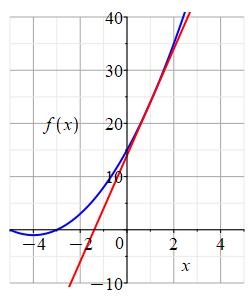
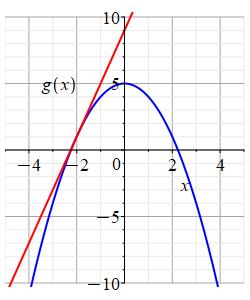
Looking at the graph of \(f\), we draw a tangent line at \(x=g(-2)=1\). Its slope is approximately \(f'(g(-2))=f'(1)\approx10\). (The tangent line passes through the points \((-2,-6)\) and \((2,34)\). Compute the slope.) So \[ (f\circ g)'(-2)=f'(g(-2))g'(-2)\approx(10)(4)=40 \]
Find the derivative of \(z\) with respect to \(x\) for \(z=\cos(y)\) and \(y=\sin(x)\).
\(\dfrac{dz}{dx}=-\sin(\sin(x))\cos(x)\)
The Chain Rule gives \(\dfrac{dz}{dx}=\dfrac{dz}{dy}\dfrac{dy}{dx}\).
First, we find the information we need for the formula: \[ \dfrac{dz}{dy}=-\sin(y)\qquad\dfrac{dy}{dx}=\cos(x) \]
We then plug these values into the formula for the Chain Rule: \[ \dfrac{dz}{dx}=-\sin(y)\cos(x) \]
Then we remember that the derivative of the outer function needs to be evaluated at the inner function. \[ \dfrac{dz}{dx}=-\sin(\sin(x))\cos(x) \]ad
Find \(\dfrac{dy}{dt}\) if \(y=3x^2+11x\) and \(x=4t^2+3t+6\).
\(\dfrac{dy}{dt}=192t^3+216t^2+430t+141\)
The Chain Rule gives \(\dfrac{dy}{dt}=\left.\dfrac{dy}{dx}\right|_{x(t)}\dfrac{dx}{dt}\).
First, we find the two derivatives: \[ \dfrac{dy}{dx}=6x+11\qquad\dfrac{dx}{dt}=8t+3 \] and evaluate the outer derivative at the inner function: \[ \left.\dfrac{dy}{dx}\right|_{x(t)}=6(4t^2+3t+6)+11 =24t^2+18t+47 \] We then substitute these derivatives into the Chain Rule: \[\begin{aligned} \dfrac{dy}{dt}&=(24t^2+18t+47)(8t+3) \\ &=192t^3+216t^2+430t+141 \end{aligned}\]ad
Since we have complete information, we check by computing the composition and taking its derivative directly: \[\begin{aligned} y(x(t))&=3(4t^2+3t+6)^2+11(4t^2+3t+6) \\ &=3(16t^4+9t^2+36+24t^3+48t^2+36t)+44t^2+33t+66 \\ &=48t^4+27t^2+108+72t^3+144t^2+108t+44t^2+33t+66 \\ &=48t^4+72t^3+215t^2+141t+174 \\ \dfrac{dy}{dt}&=192t^3+216t^2+430t+141 \end{aligned}\]
Find \(\dfrac{dy}{dt}\) if \(y=x^3+2x^2+x+2\) and \(x=2t^2+5t\).
\(\dfrac{dy}{dt}=48t^5+300t^4+632t^3+495t^2+104t+5\)
The Chain Rule gives \(\dfrac{dy}{dt}= \left.\dfrac{dy}{dx}\right|_{x(t)}\dfrac{dx}{dt}\).
First, we find the two derivatives: \[ \dfrac{dy}{dx}=3x^2+4x+1\qquad\dfrac{dx}{dt}=4t+5 \]
and evaluate the outer derivative at the inner function: \[\begin{aligned} \left.\dfrac{dy}{dx}\right|_{x(t)}&=3(2t^2+5t)^2+4(2t^2+5t)+1 \\ &=3(4t^4+20t^3+25t^2)+8t^2+20t+1 \\ &=12t^4+60t^3+75t^2+8t^2+20t+1 \\ &=12t^4+60t^3+83t^2+20t+1 \end{aligned}\]
We then plug these values into the formula for the Chain Rule: \[\begin{aligned} \dfrac{dy}{dt}&=(12t^4+60t^3+83t^2+20t+1)(4t+5) \\ &=48t^5+240t^4+332t^3+80t^2+4t+60t^4+300t^3+415t^2+100t+5 \\ &=48t^5+300t^4+632t^3+495t^2+104t+5 \end{aligned}\]ad
Since we have complete information, we check by computing the composition and taking its derivative directly: \[\begin{aligned} y(x(t))&=(2t^2+5t)^3+2(2t^2+5t)^2+2t^2+5t+2 \\ &=8t^6+60t^5+150t^4+125t^3+2(4t^4+20t^3+25t^2)+2t^2+5t+2 \\ &=8t^6+60t^5+150t^4+125t^3+8t^4+40t^3+50t^2+2t^2+5t+2 \\ &=8t^6+60t^5+158t^4+165t^3+52t^2+5t+2 \\ \dfrac{dy}{dt}&=48t^5+300t^4+632t^3+495t^2+104t+5 \end{aligned}\]
Find the derivative of \(y=\cos(\pi\sin(\pi x))\).
What are the outer and inner functions?
\(\dfrac{dy}{dx}=-\pi^2\sin(\pi \sin(\pi x))\cos(\pi x)\)
We identify the outer function as \(y(u)=\cos(\pi u)\) and the inner function as \(u(x)=\sin(\pi x)\). ( other splits are possible.) Then the Chain Rule gives: \[ \dfrac{dy}{dx}=\left.\dfrac{dy}{du}\right|_{u(x)}\dfrac{du}{dx} \] First, we find the derivatives: \[ \dfrac{dy}{du}=-\pi\sin(\pi u) \qquad \dfrac{du}{dx}=\pi\cos(\pi x) \] and evaluate the derivative of the outer function at the inner function: \[ \left.\dfrac{dy}{du}\right|_{u(x)}=-\pi\sin(\pi \sin(\pi x)) \] We use the Chain Rule: \[\begin{aligned} \dfrac{dy}{dx}&=-\pi\sin(\pi \sin(\pi x))\pi\cos(\pi x) \\ &=-\pi^2\sin(\pi \sin(\pi x))\cos(\pi x) \end{aligned}\]
ad
Find the derivative of \(y\) with respect to \(t\) for \(y=e^x\) and \(x=5t\).
\(\dfrac{dy}{dt}=5e^{5t}\)
The Chain Rule gives \(\dfrac{dy}{dt}=\left.\dfrac{dy}{dx}\right|_{x(t)} \dfrac{dx}{dt}\).
First, we find the derivatives: \[ \dfrac{dy}{dx}=e^x\qquad\dfrac{dx}{dt}=5 \] and evaluate the outer derivative at the inner function: \[ \left.\dfrac{dy}{dx}\right|_{x(t)}=e^{5t} \] We then plug these values into the formula for the Chain Rule: \[ \dfrac{dy}{dt}=e^{5t}5=5e^{5t} \]ad
Find the derivative of \(y\) with respect to \(t\) for \(y=7^x\) and \(x=5t^2+4t\).
\(\dfrac{dy}{dt}=\ln(7)7^{5t^2+4t}(10t+4)\)
The Chain Rule gives \(\dfrac{dy}{dt}=\left.\dfrac{dy}{dx}\right|_{x(t)}\dfrac{dx}{dt}\).
First, we find the derivatives: \[ \dfrac{dy}{dx}=\ln(7)7^x\qquad\dfrac{dx}{dt}=10t+4 \] and evaluate the outer derivative at the inner function: \[ \left.\dfrac{dy}{dx}\right|_{x(t)}=\ln(7)7^{5t^2+4t} \] We then plug these values into the formula for the Chain Rule: \[ \dfrac{dy}{dt}=\ln(7)7^{5t^2+4t}(10t+4) \]ad
Find the derivative of \(y\) with respect to \(t\) for \(y=4^x\) and \(x=\sin(t)\).
\(\dfrac{dy}{dt}=\cos(t)\ln(4)4^{\sin(t)}\)
The Chain Rule gives \(\dfrac{dy}{dt}=\left.\dfrac{dy}{dx}\right|_{x(t)} \dfrac{dx}{dt}\).
First, we find the derivatives: \[ \dfrac{dy}{dx}=\ln(4)4^x\qquad\dfrac{dx}{dt}=\cos(t) \]
and evaluate the outer derivative at the inner function: \[ \left.\dfrac{dy}{dx}\right|_{x(t)}=\ln(4)4^{\sin(t)} \]
We then plug these values into the formula for the Chain Rule: \[ \dfrac{dy}{dt}=\cos(t)\ln(4)4^{\sin(t)} \]ad
Differentiate \(f(x)=(x^3-4x+7)^{15}\).
Here the outer function is just a power.
\(\dfrac{df}{dx}=15(x^3-4x+7)^{14}(3x^2-4)\)
We identify the outer function as \(f(y)=y^{15}\) and the inner function as \(y(x)=x^3-4x+7\). Then the Chain Rule gives \[ \dfrac{df}{dx}=\left.\dfrac{df}{dy}\right|_{y(x)}\dfrac{dy}{dx} \] First, we find the derivatives: \[ \dfrac{df}{dy}=15y^{14}\qquad\dfrac{dy}{dx}=3x^2-4 \] and evaluate the derivative of the outer function at the inner function: \[ \left.\dfrac{df}{dy}\right|_{y(x)}=15(x^3-4x+7)^{14} \] We use the Chain Rule: \[ \dfrac{df}{dx}=15(x^3-4x+7)^{14}(3x^2-4) \]
ad
Differentiate \(g(y)=\cos(y^2)\).
\(g'(y)=-2y\sin(y^2)\)
We identify the outer function as \(g(u)=\cos(u)\) and the inner function as \(u(y)=y^2\). Their derivatives are \[ g'(u)=-\sin(u) \qquad \text{and} \qquad u'(y)=2y \] Then the Chain Rule gives: \[\begin{aligned} (g\circ u)'(y)&=g'(u(y))u'(y) \\ &=-\sin(y^2)2y =-2y\sin(y^2) \end{aligned}\]
ad
Differentiate \(g(x)=\sin^2(x)\).
Remember, \(\sin^2(x)=[\sin(x)]^2\).
\(g'(x)=2\sin(x)\cos(x)=\sin(2x)\)
We identify the outer function as \(g(u)=u^2\) and the inner function as \(u(x)=\sin(x)\). Their derivatives are \[ g'(u)=2u \qquad \text{and} \qquad u'(x)=\cos(x) \] Then the Chain Rule gives: \[\begin{aligned} g'(x)&=g'(u(x))u'(x) \\ &=2\sin(x)\cos(x) =\sin(2x) \end{aligned}\] where in the last step we used the trig identity \(\sin(2x)=2\sin(x)\cos(x)\).
ad
Differentiate \(g(y)=\cos^2(y^2)\).
This is a double Chain Rule with an outer function, an intermediate function and an inner function.
\(\dfrac{dg}{dy}=-4y\cos(y^2)\sin(y^2) =-2y\sin(2y^2)\)
This is a double Chain Rule. The outer function is \(g(u)=u^2\). The intermediate function is \(u(z)=\cos(z)\) and the inner function as \(z(y)=y^2\). Their derivatives are: \[ g'(u)=2u \qquad u'(z)=-\sin(z) \qquad z'(y)=2y \] Then the Chain Rule gives \[\begin{aligned} (g\circ u\circ z)'(y)&=g'(u(z(y)))u'(z(y))z'(y) \\ &=2(\cos(y^2))(-\sin(y^2))2y \\ &=-4y\cos(y^2)\sin(y^2) =-2y\sin(2y^2) \end{aligned}\] At the end, we used a trig identity.
ad
Differentiate \(F(\theta)=\tan^2(7\theta)\).
This is a double Chain Rule with an outer function, an intermediate function and an inner function.
\(F'(\theta)=14\tan(7\theta)\sec^2(7\theta)\)
This is a double Chain Rule. The outer function is \(F(u)=u^2\). The intermediate function is \(u(j)=\tan(j)\) and the inner function as \(j(\theta)=7\theta\). So that \[ (F\circ u\circ j)(y)=[\tan(7\theta)]^2 \] Then their derivatives are: \[ F'(u)=2u \qquad u'(j)=\sec^2(j) \qquad j'(\theta)=7 \] And the Chain Rule gives: \[\begin{aligned} (F\circ u\circ j)'(\theta)&=F'(u(j(\theta)))u'(j(\theta))j'(\theta) \\ &=2[\tan(7\theta)][\sec^2(7\theta)]7 \\ &=14\tan(7\theta)\sec^2(7\theta) \end{aligned}\]
ad
Differentiate \(w(\theta)=\csc^2(\cot\theta)\).
This is a double Chain Rule with an outer function, an intermediate function and an inner function.
\(\dfrac{dw}{d\theta}=2\csc^2(\cot\theta)\cot(\cot\theta)\csc^2\theta\)
This is a double Chain Rule. The outer function is squaring and the intermediate function is \(\csc\) and the inner function is \(\cot\). To apply the Chain Rule we differentiate the outer function and evaluate it at the intermediate function composed with the inner function and then multiply by the derivative of the intermediate function and evaluate it at the inner function and then multiply by the derivative of the inner function: \[\begin{aligned} w'(\theta)&=2\csc(\cot\theta)\cdot[-\csc(\cot\theta)\cot(\cot\theta)]\cdot (-\csc^2\theta) \\ &=2\csc^2(\cot\theta)\cot(\cot\theta)\csc^2\theta \end{aligned}\]
ad
Differentiate \(z(x)=\sin^2(\cos^2(x))\).
\(\begin{aligned} z'(x)&=-4\sin(\cos^2(x))\cos(\cos^2(x))\cos(x)\sin(x) \\ &=-\sin(2\cos^2(x))\sin(2x) \end{aligned}\)
It is useful to rewrite the function as: \[ z(x)=[\sin([\cos(x)]^2)]^2 \] There are \(4\) levels of functions: squaring, \(\sin\), squaring and \(\cos\). To apply the Chain Rule we differentiate each level of function and evaluate at the inside function. Then we multiply them together: \[\begin{aligned} z'(x)&=2[\sin([\cos(x)]^2)]\cdot[\cos([\cos(x)]^2)]\cdot2[\cos(x)]\cdot[-\sin(x)] \\ &=-4\sin(\cos^2(x))\cos(\cos^2(x))\cos(x)\sin(x) \\ &=-\sin(2\cos^2(x))\sin(2x) \end{aligned}\] At the end, we used a trig identity, twice.
ad
Differentiate \(g(t)=\cos^2(t)\).
\(g'(t)=-2\sin(t)\cos(t)=-\sin(2t)\)
The outer function is squaring and the inner function is \(\cos\). To apply the Chain Rule we differentiate the outer function and evaluate it at the inner function and then multiply by the derivative of the inner function: \[\begin{aligned} g'(t)&=2\cos(t)[-\sin(t)] \\ &=-2\sin(t)\cos(t) =-\sin(2t) \end{aligned}\] At the end, we used a trig identity.
ad
Differentiate \(f(y)=\cot^2(y)\).
\(f'(y)=-2\cot(y)\csc^2(y)\)
The outer function is squaring and the inner function is \(\cot\). To apply the Chain Rule we differentiate the outer function and evaluate it at the inner function and then multiply by the derivative of the inner function: \[ f'(y)=2\cot(y)\cdot(-\csc^2(y))=-2\cot(y)\csc^2(y) \]
ad
Use the previous two problems to differentiate \(z(t)=\cot^2(\cos^2(t))\).
In previous two problems we found: \[ \dfrac{d}{dy}(\cot^2(y))=-2\cot(y)\csc^2(y) \] \[ \dfrac{d}{dy}(\cos^2(y))=-\sin(2y) \] Use these as the outer and inner functions.
\(z'(t)=2\cot(\cos^2(t))\csc^2(\cos^2(t))\sin(2t)\)
Notice that \(z(t)=f(g(t))\) where \(f(y)=\cot^2(y)\) and \(g(t)=\cos^2(t)\). We use these as the outer and inner functions. In previous two problems we found: \[ f'(y)=-2\cot(y)\csc^2(y) \] \[ g'(t)=-\sin(2t) \] To apply the Chain Rule, we evaluate \(f'(y)\) at \(y=g(t)\) and multiply \(g'(t)\): \[\begin{aligned} z'(t)&=-2\cot(\cos^2(t))\csc^2(\cos^2(t))\cdot(-\sin(2t)) \\ &=2\cot(\cos^2(t))\csc^2(\cos^2(t))\sin(2t) \end{aligned}\]
ad
If \(f(x)=\sin(5^x)\), find \(\dfrac{df}{dx}\).
\(f'(x)=5^x\ln(5)\cos(5^x)\)
The outer function is \(\sin\) and the inner function is \(5^x\). To apply the Chain Rule we differentiate the outer function and evaluate it at the inner function and then multiply by the derivative of the inner function: \[ f'(x)=\cos(5^x)\ln(5)5^x=5^x\ln(5)\cos(5^x) \]
ad
If \(g(y)=\sec(\sin(y))\), find \(\dfrac{dg}{dy}\).
\(g'(y)=\sec(\sin(y))\tan(\sin(y))\cos(y)\)
The outer function is \(\sec\) and the inner function is \(\sin\). To apply the Chain Rule we differentiate the outer function and evaluate it at the inner function and then multiply by the derivative of the inner function: \[ g'(y)=\sec(\sin(y))\tan(\sin(y))\cos(y) \]
ad
If \(f(y)=\sin(y^2+2y+2)\), find \(\dfrac{df}{dy}\).
\(f'(y)=\cos(y^2+2y+2)(2y+2)\)
The outer function is \(\sin\) and the inner function is \(y^2+2y+2\). To apply the Chain Rule we differentiate the outer function and evaluate it at the inner function and then multiply by the derivative of the inner function: \[ f'(y)=\cos(y^2+2y+2)(2y+2) \]
ad
If \(g(x)=\cot(\sin(x))\), find \(\dfrac{dg}{dx}\).
\(g'(x)=-\csc^2(\sin(x))\cos(x)\)
The outer function is \(\cot\) and the inner function is \(\sin\). To apply the Chain Rule we differentiate the outer function and evaluate it at the inner function and then multiply by the derivative of the inner function: \[ g'(x)=-\csc^2(\sin(x))\cos(x) \]
ad
If \(f(x)=\tan((x^2+2x+2)^{50})\), find \(\dfrac{df}{dx}\).
\(f'(x)=100(x+1)(x^2+2x+2)^{49}\sec^2((x^2+2x+2)^{50})\)
This is a double Chain Rule. The outer function is \(\tan\) and the intermediate function is \(u^{50}\) and the inner function is \(u=x^2+2x+2\). To apply the Chain Rule we differentiate the outer function and evaluate it at the intermediate function composed with the inner function and then multiply by the derivative of the intermediate function at the inner function and then multiply by the derivative of the inner function. \[\begin{aligned} f'(x)&=\sec^2((x^2+2x+2)^{50})50(x^2+2x+2)^{49}(2x+2) \\ &=100(x+1)(x^2+2x+2)^{49}\sec^2((x^2+2x+2)^{50}) \end{aligned}\]
ad
If \(r(\theta)=(\sin^3(\theta)+\cos(2\theta))^{12}\), find \(\dfrac{dr}{d\theta}\).
Use the Chain Rule, then the sum Rule and the Chain Rule.
\(r'(\theta)=12[\sin^3(\theta)+\cos(2\theta)]^{11}[3\sin^2(\theta) \cos(\theta)-2\sin(2\theta)]\)
The outer function is \(x^{12}\) and the inner function is \(x=\sin^3(\theta)+\cos(2\theta)\). The derivative of the outer function is \(12x^{11}\). To calculate the derivative of the inner function we use the Sum Rule and then the Chain Rule: \[\begin{aligned} \dfrac{dx}{d\theta}&=\dfrac{d}{d\theta}(\sin^3(\theta)+\cos(2\theta)) \\ &=\dfrac{d}{d\theta}(\sin^3(\theta))+\dfrac{d}{d\theta}(\cos(2\theta)) \\ &=3\sin^2(\theta)\cos(\theta)-2\sin(2\theta) \end{aligned}\] To apply the Chain Rule to the function \(r\), we evaluate the derivative of the outer function at the inner function and then multiply by the derivative of the inner function: \[ r'(\theta)=12[\sin^3(\theta)+\cos(2\theta)]^{11}[3\sin^2(\theta) \cos(\theta)-2\sin(2\theta)] \]
ad
If \(f(x)=e^{\tan(\sin(x))+\cos^4(x)}\), find \(\dfrac{df}{dx}\).
Use the Chain Rule, then the Sum Rule and the Chain Rule.
\(f'(x)=e^{\tan(\sin(x))+\cos^4(x)}(\sec^2(\sin(x))\cos(x)-4\cos^3(x) \sin(x))\)
The outer function is \(e^y\) and the inner function is \(y=\tan(\sin( x))+\cos^4(x)\). The derivative of the outer function is \(e^y\). To calculate the derivative of the inner function we use the Sum Rule and then the Chain Rule: \[\begin{aligned} \dfrac{dy}{dx}&=\dfrac{d}{dx}(\tan(\sin(x))+\cos^4(x)) \\ &=\dfrac{d}{dx}(\tan(\sin(x)))+\dfrac{d}{dx}(\cos^4(x)) \\ &=\sec^2(\sin(x))\cos(x)-4\cos^3(x)\sin(x) \end{aligned}\] To apply the Chain Rule to the function \(f\), we evaluate the derivative of the outer function at the inner function and multiply by the derivative of the inner function: \[ f'(x)=e^{\tan(\sin(x))+\cos^4(x)}(\sec^2(\sin(x))\cos(x)-4\cos^3(x)\sin( x)) \]
ad
If \(f(x)=(5^{\sin(x)}+e^{\cot(x)})^{100}\), find \(f'(x)\).
\(f'(x)=100(5^{\sin(x)}+e^{\cot(x)})^{99} \left[\rule{0pt}{10pt}\ln(5)5^{\sin(x)}\cos(x)-e^{\cot(x)}\csc^2(x)\right]\)
The outer function is \(u^{100}\) and the inner function is \(u=5^{\sin( x)}+e^{\cot(x)}\). The derivative of the outer function is \(100u^{99}\). To calculate the derivative of the inner function we use the Sum Rule and then the Chain Rule: \[\begin{aligned} u'(x)&=\dfrac{d}{dx}(5^{\sin(x)}+e^{\cot(x)}) \\ &=\dfrac{d}{dx}(5^{\sin(x)})+\dfrac{d}{dx}(e^{\cot(x)}) \\ &=\ln(5)5^{\sin(x)}\cos(x)-e^{\cot(x)}\csc^2(x) \end{aligned}\] To apply the Chain Rule to the function \(f\) we evaluate the derivative of the outer function at the inner function and multiply by the derivative of the inner function: \[ f'(x)=100(5^{\sin(x)}+e^{\cot(x)})^{99} \left[\rule{0pt}{10pt}\ln(5)5^{\sin(x)}\cos(x)-e^{\cot(x)}\csc^2(x)\right] \]
ad
All the steps can and should be done in a single computation: \[\begin{aligned} f'(x)&=100(5^{\sin(x)}+e^{\cot(x)})^{99}\dfrac{d}{dx} \left[\rule{0pt}{10pt}5^{\sin(x)}+e^{\cot(x)} \right] \\ &=100(5^{\sin(x)}+e^{\cot(x)})^{99} \left[\rule{0pt}{10pt}\dfrac{d}{dx}\left(5^{\sin(x)}\right) +\dfrac{d}{dx}\left(e^{\cot(x)}\right) \right] \\ &=100(5^{\sin(x)}+e^{\cot(x)})^{99} \left[\rule{0pt}{10pt}\ln(5)5^{\sin(x)}\cos(x)-e^{\cot(x)}\csc^2(x)\right] \end{aligned}\]
If \(f(x)=\sin[\sin(x)\tan(2x)]\), find \(f'(x)\).
Use the Chain Rule, then the product Rule and the Chain Rule. Try to do it all in one computation.
\(f'(x)=\cos(\sin(x)\tan(2x))[2\sin(x)\sec^2(2x)+\tan(2x)\cos(x)]\)
The outer function is \(\sin\) and the inner function is \(\sin(x)\tan(2x)\). The derivative of the outer function is \(\cos\). To calculate the derivative of the inner function we use the Product Rule and then the Chain Rule: \[\begin{aligned} f'(x)&=\cos[\sin(x)\tan(2x)]\dfrac{d}{dx}[\sin(x)\tan(2x)] \\ &=\cos[\sin(x)\tan(2x)]\left[\sin(x)\dfrac{d}{dx}(\tan(2x))+\tan(2x) \dfrac{d}{dx}(\sin(x))\right] \\ &=\cos[\sin(x)\tan(2x)]\left[2\sin(x)\sec^2(2x)+\tan(2x)\cos(x)\right] \end{aligned}\]
ad
If \(f(x)=\sin[3^{\sin(x)}\cos(\cos(x))]\), find \(f'(x)\).
Use the Chain Rule, then the product Rule and the Chain Rule. Try to do it all in one computation.
\(\begin{aligned} f'(x)&=\cos[3^{\sin(x)}\cos(\cos(x))] \\ &\quad\cdot3^{\sin(x)}\left[\sin(\cos(x))\sin(x)+\cos(\cos(x))\ln(3)\cos(x)\right] \end{aligned}\)
The outer function is \(\sin\) and the inner function is \(3^{\sin(x)}\cos(\cos(x))\). The derivative of the outer function is \(\cos\). To calculate the derivative of the inner function, we use the Product Rule and then the Chain Rule: \[\begin{aligned} f'(x)&=\cos[3^{\sin(x)}\cos(\cos(x))] \dfrac{d}{dx}[3^{\sin(x)}\cos(\cos(x))] \\ &=\cos[3^{\sin(x)}\cos(\cos(x))] \\ &\quad\cdot\left[3^{\sin(x)}\dfrac{d}{dx}\big(\cos(\cos(x))\big) +\cos(\cos(x))\dfrac{d}{dx}\big(3^{\sin(x)}\big)\right] \\ &=\cos[3^{\sin(x)}\cos(\cos(x))] \\ &\quad\cdot\left[3^{\sin(x)}\sin(\cos(x))\sin(x) +\cos(\cos(x))\ln(3)3^{\sin(x)}\cos(x)\right] \\ &=\cos[3^{\sin(x)}\cos(\cos(x))] \\ &\quad\cdot3^{\sin(x)}\left[\sin(\cos(x))\sin(x)+\cos(\cos(x))\ln(3)\cos(x)\right] \end{aligned}\]
ad
If \(f(x)=\cos\left(\dfrac{3^x}{\sin(x^5)}\right)\), find \(f'(x)\).
Use the Chain Rule, then the Quotient Rule and the Chain Rule. Try to do it all in one computation.
\(f'(x)=-\sin\left(\dfrac{3^x}{\sin(x^5)}\right)3^x \dfrac{\ln(3)\sin(x^5)-5x^4\cos(x^5)}{\sin^2(x^5)}\)
The outer function is \(\cos\) and the inner function is \(\dfrac{3^x}{ \sin(x^5)}\). The derivative of the outer function is \(-\sin\). To calculate the derivative of the inner function we use the Quotient Rule and then the Chain Rule: \[\begin{aligned} f'(x)&=-\sin\left(\dfrac{3^x}{\sin(x^5)}\right) \dfrac{d}{dx}\left(\dfrac{3^x}{\sin(x^5)}\right) \\ &=-\sin\left(\dfrac{3^x}{\sin(x^5)}\right) \dfrac{\sin(x^5)\dfrac{d}{dx}(3^x)-3^x\dfrac{d}{dx}(\sin(x^5))}{\sin^2(x^5)} \\ &=-\sin\left(\dfrac{3^x}{\sin(x^5)}\right) \dfrac{\sin(x^5)\ln(3)3^x-3^x\cos(x^5)5x^4}{\sin^2(x^5)} \\ &=-\sin\left(\dfrac{3^x}{\sin(x^5)}\right)3^x \dfrac{\ln(3)\sin(x^5)-5x^4\cos(x^5)}{\sin^2(x^5)} \end{aligned}\] \]
ad
If \(u(v)=\sin^{23}\left(3^x+\dfrac{v^4}{\sin(2v)}\right)\), find \(u'(v )\).
Use the Chain, Sum, Quotient, and Chain Rules. This is also a double Chain Rule. Try to do it all in one computation.
\(\begin{aligned} u'(v)&=23\sin^{22}\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \cos\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \\ &\quad\cdot \left(\ln(3)3^x +\dfrac{4v^3\sin(2v)-2v^4\cos(2v)}{\sin^2(2v)}\right) \\ \end{aligned}\)
This is a double Chain Rule. The outer function is \(s^{23}\) and the intermediate function is \(s=\sin(w)\) and the inner function is \(w=3^x+\dfrac{v^4}{\sin(2v)}\). The derivatives of the outer and intermediate functions are \(23s^{22}\) and \(\cos\), respectively. To calculate the derivative of the inner function we use the Sum Rule, Exponential Rule, Quotient Rule and then the Chain Rule: \[\begin{aligned} u'(v)&=23\sin^{22}\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \dfrac{d}{dv}\sin\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \\ &=23\sin^{22}\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \cos\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \dfrac{d}{dv}\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \\ &=23\sin^{22}\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \cos\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \\ &\quad\cdot \left(\ln(3)3^x +\dfrac{\sin(2v)\dfrac{d}{dv}[v^4]-v^4\dfrac{d}{dv}[\sin(2v)]}{\sin^2(2v)}\right) \\ &=23\sin^{22}\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \cos\left(3^x+\dfrac{v^4}{\sin(2v)}\right) \\ &\quad\cdot \left(\ln(3)3^x +\dfrac{4v^3\sin(2v)-2v^4\cos(2v)}{\sin^2(2v)}\right) \end{aligned}\]
ad
Do the Tutorial until you feel confident.
Find the derivative of the implicitly defined function.
If \(x\) and \(y\) are related by \(x^2+2xy+y=13\), find the derivative of \(y\) with respect to \(x\) at \((1,4)\).
Regard \(y\) as a function of \(x\) as you differentiate. \[ x^2+2xy_{(x)}+y_{(x)}=13 \]
\(\left.\dfrac{dy}{dx}\right|_{(1,4)}=-\dfrac{10}{3}\)
We regard \(y\) as a function of \(x\) as we differentiate. \[ x^2+2xy_{(x)}+y_{(x)}=13 \] We differentiate both sides with respect to \(x\), using the Sum and Product Rules: \[ 2x+2x\dfrac{dy}{dx}+2y+\dfrac{dy}{dx}=0 \] Now we evaluate at \((x,y)=(1,4)\) and solve for the derivative: \[\begin{aligned} 2+2\dfrac{dy}{dx}+8+\dfrac{dy}{dx}&=0 \\ 10+3\dfrac{dy}{dx}&=0 \\ \left.\dfrac{dy}{dx}\right|_{(1,4)}&=-\dfrac{10}{3} \end{aligned}\]
ad
If \(x\) and \(y\) are related by \(x^3+3x^2y+3xy+y^3=89\), find the derivative of \(x\) with respect to \(y\), \(\dfrac{dx}{dy}\), at \((x,y)=(2,3)\).
This time regard \(x\) as a function of \(y\) as you differentiate. \[ x_{(y)}^3+3x_{(y)}^2y+3x_{(y)}y+y^3=89 \]
\(\left.\dfrac{dx}{dy}\right|_{(2,3)}=-\dfrac{15}{19}\)
This time we regard \(x\) as a function of \(y\) as we differentiate. \[ x_{(y)}^3+3x_{(y)}^2y+3x_{(y)}y+y^3=89 \] We differentiate both sides with respect to \(y\), using the Sum, Power, Product and Chain Rules: \[ 3x^2\dfrac{dx}{dy}+3x^2+6xy\dfrac{dx}{dy}+3x+3y\dfrac{dx}{dy}+3y^2=0 \] Now we evaluate at \((x,y)=(2,3)\) and solve for the derivative: \[\begin{aligned} 12\dfrac{dx}{dy}+12+36\dfrac{dx}{dy}&+6+9\dfrac{dx}{dy}+27=0 \\ 57\dfrac{dx}{dy}+45&=0 \\ \left.\dfrac{dx}{dy}\right|_{(2,3)} &=-\dfrac{45}{57}=-\dfrac{15}{19} \end{aligned}\]
ad
If \(y\) and \(z\) are related by \(y^2+2y\sin\left(\dfrac{\pi z}{2}\right)+\sin(\pi z)=3\), find the derivative of \(z\) with respect to \(y\) at \((y,z)=(3,3)\).
This time regard \(z\) as a function of \(y\) as you differentiate. \[ y^2+2y\sin\left(\dfrac{\pi z_{(y)}}{2}\right)+\sin(\pi z_{(y)})=3 \]
\(\left.\dfrac{dz}{dy}\right|_{(3,3)}=\dfrac{4}{\pi}\)
This time we regard \(z\) as a function of \(y\) as we differentiate. \[ y^2+2y\sin\left(\dfrac{\pi z_{(y)}}{2}\right)+\sin(\pi z_{(y)})=3 \] We apply \(\dfrac{d}{dy}\) to both sides, using the Sum, Power, Product and Chain Rules: \[ 2y+\pi y\cos\left(\dfrac{\pi z}{2}\right)\dfrac{dz}{dy} +2\sin\left(\dfrac{\pi z}{2}\right)+\pi\cos(\pi z)\dfrac{dz}{dy}=0 \] Now we evaluate at \((y,z)=(3,3)\) and solve for the derivative: \[\begin{aligned} 6-2-\pi\dfrac{dz}{dy}&=0 \\ 4-\pi\dfrac{dz}{dy}&=0 \\ \left.\dfrac{dz}{dy}\right|_{(3,3)}&=\dfrac{4}{\pi} \end{aligned}\]
ad
If \(x\) and \(y\) are related by \(x^2y+y^2x=6\), find \(\dfrac{dy}{dx}\) at \((1,2)\).
\(\left.\dfrac{dy}{dx}\right|_{(1,2)}=-\,\dfrac{8}{5}\)
We differentiate both sides, using the Sum, Product, Power and Chain Rules: \[ x^2\dfrac{dy}{dx}+2xy+y^2+2xy\dfrac{dy}{dx}=0 \] Now we evaluate at \((x,y)=(1,2)\) and solve for the derivative: \[\begin{aligned} \dfrac{dy}{dx}+4+4+4\dfrac{dy}{dx}&=0 \\ 5\dfrac{dy}{dx}+8&=0 \\ \left.\dfrac{dy}{dx}\right|_{(1,2)}&=-\,\dfrac{8}{5} \end{aligned}\]
ad
If \(y\) and \(z\) are related by \(y^2+z^2=24-y^2z^2\), find \(\dfrac{dz}{dy}\) at \((y,z)=(2,2)\).
\(\left.\dfrac{dz}{dy}\right|_{(2,2)}=-1\)
We apply \(\dfrac{d}{dy}\) to both sides, using the Sum, Power, Product and Chain Rules: \[ 2y+2z\dfrac{dz}{dy}=-2y^2z\dfrac{dz}{dy}-2yz^2 \] Now we evaluate at \((y,z)=(2,2)\) and solve for the derivative: \[\begin{aligned} 4+4\dfrac{dz}{dy}&=-16\dfrac{dz}{dy}-16 \\ 20\dfrac{dz}{dy}&=-20 \\ \left.\dfrac{dz}{dy}\right|_{(2,2)}&=-1 \end{aligned}\]
ad
If \(x\) and \(z\) are related by \(x^2+z^2+\cos(\pi xz)=14\), find \(\dfrac{dz}{dx}\) at \((x,z)=(2,3)\).
\(\left.\dfrac{dz}{dx}\right|_{(2,3)}=-\dfrac{2}{3}\)
We differentiate both sides, using the Sum, Power, Chain, and Product Rules: \[ 2x+2z\dfrac{dz}{dx}-\sin(\pi xz)\pi\left(x\dfrac{dz}{dx}+z\right)=0 \] Now we evaluate at \((x,z)=(2,3)\) and solve for the derivative: \[\begin{aligned} 4+6\dfrac{dz}{dx}&=0 \\ \left.\dfrac{dz}{dx}\right|_{(2,3)}&=-\dfrac{4}{6}=-\dfrac{2}{3} \end{aligned}\]
ad
If \(x\) and \(z\) are related by \(2^x+2^z=6\), find \(\dfrac{dz}{dx}\) at \((x,z)=(1,2)\).
\(\left.\dfrac{dz}{dx}\right|_{(1,2)}=-\dfrac{1}{2}\)
We differentiate both sides, using the Sum and Exponential Rules: \[ 2^x\ln(2)+2^z\ln(2)\dfrac{dz}{dx}=0 \] Now we evaluate at \((x,z)=(1,2)\) and solve for the derivative: \[\begin{aligned} 2\ln(2)+4\ln(2)\dfrac{dz}{dx}&=0 \\ 4\dfrac{dz}{dx}&=-2 \\ \left.\dfrac{dz}{dx}\right|_{(1,2)}&=-\dfrac{1}{2} \end{aligned}\]
ad
In this equation we can solve for \[ z=\log_2\left(6-2^x\right) \] So we can differentiate explicitly: \[ \dfrac{dz}{dx}=\dfrac{1}{\ln(2)}\dfrac{-\ln(2)2^x}{6-2^x} =\dfrac{-2^x}{6-2^x} \] \[ \left.\dfrac{dz}{dx}\right|_{x=1}=\dfrac{-2}{6-2}=-\dfrac{1}{2} \] But implicit differentiation was easier.
For an ideal gas the pressure \(P\) and the volume \(V\) are related by \(PV=K\) for some constant \(K\). Currently, the pressure of a sample in a box is \(P=1.1\,\text{atm}\) and the volume is \(V=15\,\text{m}^3\). Find the rate of change of the pressure with respect to the volume.
\(\left.\dfrac{dP}{dV}\right|_{(15\,\text{m}^3,1.1\,\text{atm})} =-\,\dfrac{1.1\,\text{atm}}{15\,\text{m}^3} =-.0733\dfrac{\text{atm}}{\text{m}^3}\)
We apply \(\dfrac{d}{dV}\) to both sides using the Product Rule, and solve for \(\dfrac{dP}{dV}\): \[\begin{aligned} P+V\dfrac{dP}{dV}&=0 \\ \dfrac{dP}{dV}&=-\,\dfrac{P}{V} \end{aligned}\] Now we evaluate at \((V,P)=(15\,\text{m}^3,1.1\,\text{atm})\): \[ \left.\dfrac{dP}{dV}\right|_{(15\,\text{m}^3,1.1\,\text{atm})} =-\,\dfrac{1.1\,\text{atm}}{15\,\text{m}^3} =-.0733\dfrac{\text{atm}}{\text{m}^3} \]
ad
In this equation we can solve for \[ P=\dfrac{K}{V} \] So we can differentiate explicitly using the Power Rule and substitute \(K=PV\): \[ \dfrac{dP}{dV}=-\dfrac{K}{V^2}=-\dfrac{P}{V} \]
A boy is running such that the relationship between his position, \(x\), and the time, \(t\), is \(x^3+t^3=K\) for some constant \(K\). Currently, the position is \(x=10\,\text{m}\) and the time is \(t=12\,\text{sec}\). Find his velocity at \(t=12\,\text{sec}\).
\(v(12)=\dfrac{dx}{dt} =-1.44\dfrac{\text{m}}{\text{sec}}\)
We apply \(\dfrac{d}{dt}\) to both sides, using the Sum Rule, the Power Rule, and the Chain Rule, and solve for \(v=\dfrac{dx}{dt}\): \[\begin{aligned} 3x^2\dfrac{dx}{dt}+3t^2&=0 \\ v=\dfrac{dx}{dt}&=-\,\dfrac{t^2}{x^2} \end{aligned}\] Now we evaluate at \(t=12\,\text{sec}\) and \(x=10\,\text{m}\): \[ v(12)=\dfrac{dx}{dt} =-\,\dfrac{144}{100} =-1.44\dfrac{\text{m}}{\text{sec}} \]
ad
In this equation we can solve for \[ x=\sqrt[\scriptstyle3]{K-t^3} \] So we can differentiate explicitly using the Chain and Difference and Power Rules and substitute \(K=x^3+t^3\): \[\begin{aligned} \dfrac{dx}{dt} &=\dfrac{1}{3}\dfrac{-3t^2}{(K-t^3)^{2/3}} =-\,\dfrac{t^2}{(K-t^3)^{2/3}} \\ &=-\,\dfrac{t^2}{(x^3)^{2/3}} =-\,\dfrac{t^2}{x^2} \end{aligned}\] But implicit differentiation was easier.
Two charges, \(q_1\), and \(q_2\), are repelling each other. The distance between them, \(r\), and the force, \(F\), are related by \(r^2F=kq_1q_2\) and where \(k\) is Coulomb's constant. When \(r=2\,\text{m}\) the force is \(F=15\,\text{N}\), what is the rate of change of \(r\) with respect to \(F\)?
\(\left.\dfrac{dr}{dF}\right|_{(15,2)} =-\,\dfrac{1}{15}\dfrac{\text{m}}{\text{N}}\)
We apply \(\dfrac{d}{dF}\) to both sides, using the the Power Rule and solve for \(\dfrac{dr}{dF}\): \[\begin{aligned} r^2&+F2r\dfrac{dr}{dF}=0 \\ &\dfrac{dr}{dF}=-\,\dfrac{r}{2F} \end{aligned}\] Now we evaluate at \((F,r)=(15\,\text{N},2\,\text{m})\): \[ \left.\dfrac{dr}{dF}\right|_{(15,2)} =-\,\dfrac{1}{15}\dfrac{\text{m}}{\text{N}} \]
ad
Let \(x\) be the position on a rod measured from one end. The total mass between \(x=0\) and \(x=a\) is \(m\). They are related by \(\dfrac{m^3}{a^2}=K\) for some constant \(K\). When \(a=3\,\text{m}\), we have \(m=0.02\,\text{kg}\). What is the rate of change of \(m\) with respect to \(a\) (which may be interpreted as the density of the rod at the point \(x=a\))?
\(\left.\dfrac{dm}{dx}\right|_{(3,0.02)} =.0044\overline{4}\,\dfrac{\text{kg}}{\text{m}}\)
We apply \(\dfrac{d}{da}\) to both sides using the Quotient Rule and solve for \(\dfrac{dm}{da}\): \[\begin{aligned} \dfrac{a^2 3m^2\dfrac{dm}{da}-m^3 2a}{a^4}&=0 \\ 3a\dfrac{dm}{da}-2m&=0 \\ \dfrac{dm}{da}=\dfrac{2m}{3a}& \end{aligned}\] Now we evaluate at \((a,m)=(3\,\text{m},0.02\,\text{kg})\): \[ \left.\dfrac{dm}{da}\right|_{(3,0.02)} =\dfrac{0.04}{9}\dfrac{\text{kg}}{\text{m}} =.0044\overline{4}\,\dfrac{\text{kg}}{\text{m}} \]
ad
For a pendulum, the period \(T\) in \(\text{sec}\) and the length \(L\) in \(\text{m}\) are related by \(\dfrac{T^2}{L}=K\) where \(K\) is a constant. On the surface of the Earth, \(k\approx4\). So when \(L=9\,\text{m}\) we have \(T=6\,\text{sec}\). What is \(\dfrac{dT}{dL}\) when \(L=9\,\text{m}\)?
\( \left.\dfrac{dT}{dL}\right|_{(9,6)}=\dfrac{1}{3}\,\dfrac{\text{sec}}{\text{m}}\)
We apply \(\dfrac{d}{dL}\) to both sides and solve for \(\dfrac{dT}{dL}\): \[\begin{aligned} \dfrac{L2T\dfrac{dT}{dL}-T^2}{L^2}&=0 \\ \dfrac{dT}{dL}=\dfrac{T^2}{L2T}&=\dfrac{T}{2L} \end{aligned}\] Now we evaluate at \((L,T)=\left(9\,\text{m},6\,\text{sec}\right)\): \[ \left.\dfrac{dT}{dL}\right|_{(9,6)}=\dfrac{6}{2\cdot9} =\dfrac{1}{3}\,\dfrac{\text{sec}}{\text{m}} \]
ad
In this equation we can solve for: \[ T=\sqrt{K}\sqrt{L}=2\sqrt{L} \] So we can differentiate explicitly: \[\begin{aligned} \dfrac{dT}{dL}&=\dfrac{2}{2\sqrt{L}}=\dfrac{1}{\sqrt{L}} \\ \left.\dfrac{dT}{dL}\right|_{(9,6)}&=\dfrac{1}{3} \\ \end{aligned}\]
A rod is heating up. The length \(L\) and the temperature \(T\) are related by \(\dfrac{L-L_o}{T-T_o}=\alpha L_o\) where \(\alpha\) is the coefficient of linear expansion. The original temperature is \(T_o=25\,^{\circ}\text{C}\) and the original length is \(L_o=2\,\text{m}\). If currently, \(T=50^\circ\text{C}\) and \(L=3\,\text{m}\) and, what is \(\dfrac{dL}{dT}\)?
\(\left.\dfrac{dL}{dT}\right|_{(50,3)} =\dfrac{1}{25}\,\dfrac{\text{m}}{^{\circ}\text{C}} =0.04\,\dfrac{\text{m}}{^{\circ}\text{C}}\)
We apply \(\dfrac{d}{dT}\) to both sides using the Quotient Rule and solve for \(\dfrac{dL}{dT}\): \[\begin{aligned} \dfrac{(T-T_o)\dfrac{dL}{dT}-(L-L_o)}{(T-T_o)^2}&=0 \\ (T-T_o)\dfrac{dL}{dT}-(L-L_o)&=0 \\ \dfrac{dL}{dT}=\dfrac{L-L_o}{T-T_o} \end{aligned}\] We now evaluate at \((T,L)=(50^\circ\text{C},3\,\text{m})\) with \((T_o,L_o)=(25^\circ\text{C},2\,\text{m})\): \[\begin{aligned} \left.\dfrac{dL}{dT}\right|_{(50,3)} &=\dfrac{3-2}{50-25} \\ &=\dfrac{1}{25}\,\dfrac{\text{m}}{^{\circ}\text{C}} =0.04\,\dfrac{\text{m}}{^{\circ}\text{C}} \end{aligned}\]
ad
In this equation we can solve for: \[ L=\alpha L_o(T-T_o)+L_o \] So we can differentiate explicitly: \[ \dfrac{dL}{dT}=\alpha L_o \] However, the original equation says \(\dfrac{L-L_o}{T-T_o}=\alpha L_o\). So this derivative agrees with the answer in the solution: \[ \dfrac{dL}{dT}=\dfrac{L-L_o}{T-T_o} \]
If \(x\) and \(z\) are related by \(3x^2+z^2=21\), find the equation of the tangent line at \((x,z)=(2,-3)\).
If the point of tangency is \((x_o,z_o)\) and the slope is \(m\), the point-slope equation of the tangent line is: \(z=z_o+m(x-x_o)\). Use implicit differentiation to find the slope, \(m=\left.\dfrac{dz}{dx}\right|_{(x_o,z_o)}\).
ad
\(\left.\dfrac{dz}{dx}\right|_{(2,-3)}=2\)
\(\rule{0pt}{10pt}z=-3+2(x-2)=2x-7\)We find the slope using implicit differentiation. We differentiate both sides, using the Sum and Power Rules: \[ 6x+2z\dfrac{dz}{dx}=0 \] Now we evaluate at \((x,z)=(2,-3)\) and solve for the derivative: \[\begin{aligned} 12-6\dfrac{dz}{dx}&=0 \\ m=\left.\dfrac{dz}{dx}\right|_{(2,-3)}&=2 \end{aligned}\] Since the point of tangency is \((x_o,z_o)=(2,-3)\) and the slope is \(m=2\), the point-slope equation says the tangent line is: \[\begin{aligned} z&=z_o+m(x-x_o) \\ &=-3+2(x-2)=2x-7 \end{aligned}\]
ad
In this equation we can solve for: \[ z=-\sqrt{21-3x^2} \] We take the negative square root because \(z=-3\) is negative. So we can differentiate explicitly using the Chain and Power Rules: \[\begin{aligned} \dfrac{dz}{dx}&=\dfrac{3x}{\sqrt{21-3x^2}} \\ \dfrac{dz}{dx}(2)&=\dfrac{6}{3}=2 \end{aligned}\]
If \(x\) and \(z\) are related by \(xz^2=6-x^2\), find the equation of the tangent line at \((x,z)=(2,1)\).
The equation implicitly defines \(z=f(x)\). So the equation for a tangent line is \(z=f(a)+f'(a)(x-a)\).
\(\left.\dfrac{dz}{dx}\right|_{(2,1)}=-\,\dfrac{5}{4} =-1.25\)
\(z=2-\dfrac{\rule{0pt}{10pt}5}{4}(x-1) =-\,\dfrac{5}{4}x+\dfrac{13}{4}\)We find the slope using implicit differentiation. We differentiate both sides, using the Sum, Product, and Power Rules: \[ 2xz\dfrac{dz}{dx}+z^2=-2x \] Now we evaluate at \((x,z)=(2,1)\) and solve for the derivative: \[\begin{aligned} 4\dfrac{dz}{dx}+1&=-4 \\ \left.\dfrac{dz}{dx}\right|_{(2,1)}&=-\,\dfrac{5}{4} =-1.25 \end{aligned}\] The equation implicitly defines \(z\) as a function \(f(x)\). So the tangent line is \(z=f(a)+f'(a)(x-a)\). Since the point of tangency is \((x,z)=(1,2)\), we know \(f(1)=2\). We have also computed \(f'(1)=\left.\dfrac{dz}{dx}\right|_{(2,1)}=-\,\dfrac{5}{4}\). So the tangent line is \[\begin{aligned} z&=f(1)+f'(1)(x-1) =2-\dfrac{5}{4}(x-1) \\ &=-\,\dfrac{5}{4}x+\dfrac{13}{4} \end{aligned}\]
ad
If \(x\) and \(y\) are related by \(x^2+y^3=9\), find the equation of the tangent line at \((x,y)=(1,2)\).
The equation implicitly defines \(y=f(x)\). So the equation for a tangent line is \(y=f(a)+f'(a)(x-a)\).
The equation of the tangent line at \((1,2)\) is:
\(y=-\,\dfrac{1}{6}x+\dfrac{13}{6}\)Here the equation implicitly defines \(y=f(x)\). So The equation for a tangent line is \(y=f(1)+f'(1)(x-1)\). The derivative is: \[ f'(1)=\left.\dfrac{dy}{dx}\right|_{(1,2)} \] We find the slope \(\dfrac{dy}{dx}\) by implicit differentiation: \[\begin{aligned} 2x+3y^2\dfrac{dy}{dx}&=0 \\ \dfrac{dy}{dx}&=-\dfrac{2x}{3y^2} \end{aligned}\] We now evaluate at \((x,y)=(1,2)\): \[ f'(1)=\left.\dfrac{dy}{dx}\right|_{(1,2)}=-\,\dfrac{2}{12}=-\,\dfrac{1}{6} \] Since \(f(1)=2\), the tangent line is: \[\begin{aligned} y&=f(1)+f'(1)(x-1) =2-\dfrac{1}{6}(x-1) \\ &=-\,\dfrac{1}{6}x+\dfrac{13}{6} \end{aligned}\]
ad
Review Exercises
Consider the functions \(f(x)=x+4\) and \(g(x)=2x\). Compute \(g(4)\) and \(f(g(4))\).
\(g(4)=8\)
\(f(g(4))=12\)We replace the \(x\) in \(g(x)=2x\) by \(4\): \[ g(4)=2\cdot4=8 \] Next we replace the \(x\) in \(f(x)=x+4\) by \(g(4)=8\): \[ f(g(4))=8+4=12 \]
ad
If \(g(x)=\left(\dfrac{x}{x^4+1}+5^x\right)^{500}\), find \(\dfrac{dg}{dx}\).
\(g'(x)=500\left(\dfrac{x}{x^4+1}+5^x\right)^{499} \left(\dfrac{1-3x^4}{(x^4+1)^2}+\ln(5)5^x\right)\)
The outer function is \(u^{500}\) and the inner function is \(u =\dfrac{x}{x^4+1}+5^x\). The derivative of the outer function is \( 500u^{499}\). To calculate the derivative of the inner function we use the Sum, Exponential, Quotient, Sum, and Power Rules: \[\begin{aligned} &\dfrac{d}{dx}\left(\dfrac{x}{x^4+1}+5^x\right) \\ &=\dfrac{d}{dx}\left(\dfrac{x}{x^4+1}\right)+\dfrac{d}{dx}(5^x) \\ &=\dfrac{(x^4+1)\dfrac{d}{dx}(x)-x\dfrac{d}{dx}(x^4+1)}{(x^4+1)^2} +\ln(5)5^x \\ &=\dfrac{x^4+1-4x^4}{(x^4+1)^2}+\ln(5)5^x \\ &=\dfrac{1-3x^4}{(x^4+1)^2}+\ln(5)5^x \\ \end{aligned}\] To apply the Chain Rule to the function \(g\), we take the derivative of the outer function evaluated at the inner function and then multiply by the derivative of the inner function: \[ g'(x)=500\left(\dfrac{x}{x^4+1}+5^x\right)^{499} \left(\dfrac{1-3x^4}{(x^4+1)^2}+\ln(5)5^x\right) \]
ad
If \(x\) and \(y\) are related by \(x^2+2x+2y+y^2=11\), find \(\dfrac{dy}{dx}\) at \((1,2)\).
\(\left.\dfrac{dy}{dx}\right|_{(1,2)}=-\,\dfrac{2}{3}\)
We differentiate both sides, using the Sum and Power Rules: \[ 2x+2+(2+2y)\dfrac{dy}{dx}=0 \] We now evaluate at \((x,y)=(1,2)\) and solve for \(\dfrac{dy}{dx}\): \[\begin{aligned} 4+6\left.\dfrac{dy}{dx}\right|_{(1,2)}&=0 \\ \left.\dfrac{dy}{dx}\right|_{(1,2)}&=-\,\dfrac{2}{3} \end{aligned}\]
ad
- Consider the functions \(f(x)=x^2+2x+3\) and \(g(x)=2x+4\).
-
Compute \(g(1)\) and \(f(g(1))\).
\(g(1)=6\)
\(f(g(1))=51\)We replace the \(x\) in \(g(x)=2x+4\) by \(1\): \[ g(1)=2\cdot1+4=6 \] Next we replace the \(x\) in \(f(x)=x^2+2x+3\) by \(g(1)=6\): \[ f(g(1))=6^2+2\cdot6+3=36+12+3=51 \]
ad
-
Compute \(f(1)\) and \(g(f(1))\).
\(f(1)=6\)
\(g(f(1))=16\)We replace the \(x\) in \(f(x)=x^2+2x+3\) by \(1\): \[ f(1)=1^2+2\cdot1+3=1+2+3=6 \] Next we replace the \(x\) in \(g(x)=2x+4\) by \(f(x)=6\): \[ f(g(1))=2\cdot6+4=12+4=16 \]
ad
Notice that \(g(f(1))\) is not the same as \(f(g(1))\).
-
Compute \(f(g(x))\).
\(f(g(x))=4x^2+20x+27\)
We replace the \(x\) in \(f(x)=x^2+2x+3\) by \(g(x)=2x+4\): \[\begin{aligned} f(g(x))&=(2x+4)^2+2(2x+4)+3 \\ &=4x^2+16x+16+4x+8+3 \\ &=4x^2+20x+27 \end{aligned}\]
ad
Since \(f(g(x))=4x^2+20x+27\), we have \[\begin{aligned} f(g(1))&=4\cdot1^2+20\cdot1+27 \\ &=4+20+27=51 \end{aligned}\] which agrees with the answer from part (a).
-
Compute \(g(f(x))\).
\(g(f(x))=2x^2+4x+10\)
We replace the \(x\) in \(g(x)=2x+4\) by \(f(x)=x^2+2x+3\): \[\begin{aligned} g(f(x))&=2(x^2+2x+3)+4 \\ &=2x^2+4x+6+4 \\ &=2x^2+4x+10 \end{aligned}\]
ad
Since \(g(f(x))=2x^2+4x+10\), we have: \[\begin{aligned} g(f(1))&=2\cdot1^2+4\cdot1+10 \\ &=2+4+10=16 \end{aligned}\] which agrees with the answer in part (b).
Notice that \(g(f(x))\) is not equal to \(f(g(x))\).
If \(f(x)=\sin^2(\cot^2(x^3+5))\), what is \( \dfrac{df}{dx}\)?
\[\begin{aligned} f'(x)&=-12x^2\sin(\cot^2(x^3+5))\cos(\cot^2(x^3+5)) \\ &\qquad\cdot\cot(x^3+5)\csc^2(x^3+5) \end{aligned}\]
It is useful to rewrite the function as: \[ f(x)=[\sin([\cot(x^3+5)]^2)]^2 \] There are \(5\) levels of functions: squaring, \(\sin\), squaring, \(\cot\), and \(x^3+5\). To apply the Chain Rule we differentiate each level of function and multiply them: \[\begin{aligned} f'(x)&=2\sin([\cot(x^3+5)]^2)\cdot\cos([\cot(x^3+5)]^2) \\ &\qquad\cdot2\cot(x^3+5) \cdot[-\csc^2(x^3+5)]\cdot3x^2 \\ &=-12x^2\sin(\cot^2(x^3+5))\cos(\cot^2(x^3+5)) \\ &\qquad\cdot\cot(x^3+5)\csc^2(x^3+5) \end{aligned}\]
ad
If \(x\) and \(y\) are related by \(xy^2+x^2y=30\), find the equation of the tangent line at \((2,3)\).
The tangent line at \((2,3)\) is:
\(y=3-\dfrac{21}{16}(x-2)=-\,\dfrac{21}{16}x+\dfrac{45}{8}\)The equation implicitly defines a function \(y=f(x)\). Since the point of tangency is \((2,3)\), we have \(f(2)=3\) and \(f'(2)=\left.\dfrac{dy}{dx}\right|_{(2,3)}\). We compute the derivative using implicit differentiation: \[ 2xy\dfrac{dy}{dx}+y^2+x^2\dfrac{dy}{dx}+2xy=0 \] We evaluate at \((x,y)=(2,3)\) and solve: \[\begin{aligned} 12\dfrac{dy}{dx}+9+4\dfrac{dy}{dx}+12=0 \\ f'(2)=\left.\dfrac{dy}{dx}\right|_{(2,3)}=-\,\dfrac{21}{16} \end{aligned}\] So the tangent line is: \[\begin{aligned} y&=f(2)+f'(2)(x-2) =3-\dfrac{21}{16}(x-2) \\ &=-\,\dfrac{21}{16}x+\dfrac{45}{8} \end{aligned}\]
ad
If \(f(x)=\sec^3\left(x+\sqrt{x^2+1}\right)\), what is \(\dfrac{df}{dx}\)?
\(f'(x)=3\sec^3\left(x+\sqrt{x^2+1}\right)\tan\left(x+\sqrt{x^2+1}\right) \left(1+\dfrac{x}{\sqrt{x^2+1}}\right)\)
This is a triple Chain Rule. We work from the outside in. The outer function is \(u^3\) and the intermediate function is \(u=\sec(r)\) where the inner function is \(r=x+\sqrt{x^2+1}\). Then after using the Sum Rule, the outer function is square root and the inner function is \(x^2+1\). \[\begin{aligned} f'(x)&=3\sec^2\left(x+\sqrt{x^2+1}\right)\dfrac{d}{dx}\sec\left(x+\sqrt{x^2+1}\right) \\ &=3\sec^2\left(x+\sqrt{x^2+1}\right) \\ &\qquad\cdot\sec\left(x+\sqrt{x^2+1}\right)\tan\left(x+\sqrt{x^2+1}\right) \dfrac{d}{dx}\left(x+\sqrt{x^2+1}\right) \\ &=3\sec^2\left(x+\sqrt{x^2+1}\right) \\ &\qquad\cdot\sec\left(x+\sqrt{x^2+1}\right)\tan\left(x+\sqrt{x^2+1}\right) \left(1+\dfrac{x}{\sqrt{x^2+1}}\right) \\ &=3\sec^3\left(x+\sqrt{x^2+1}\right)\tan\left(x+\sqrt{x^2+1}\right) \left(1+\dfrac{x}{\sqrt{x^2+1}}\right) \end{aligned}\]
ad
If \(x\) and \(y\) are related by \(x\sin(\pi y)-y^2\cos(\pi x)=\dfrac{1}{4}\left(1-\dfrac{1}{\sqrt{2}}\right)\), find the equation of the tangent line at \(\left(\dfrac{1}{4},\dfrac{1}{2}\right)\).
The equation of the tangent line at \(\left(\dfrac{1}{4},\dfrac{1}{2}\right)\) is: \[ y=-\left(\sqrt{2}+\dfrac{\pi}{4}\right)x+\dfrac{1}{2}+\dfrac{\sqrt{2}}{4}+\dfrac{\pi}{16} \]
The equation implicitly defines a function \(y=f(x)\). Since the point of tangency is \(\left(\dfrac{1}{4},\dfrac{1}{2}\right)\), we have \(f\left(\dfrac{1}{4}\right)=\dfrac{1}{2}\) and \(f'\left(\dfrac{1}{4}\right)=\left.\dfrac{dy}{dx}\right|_{\left(\frac{1}{4},\frac{1}{2}\right)}\). We compute the derivative using implicit differentiation: \[\begin{aligned} \pi x\cos(\pi y)&\dfrac{dy}{dx}+\sin(\pi y)+\pi y^2\sin(\pi x)+2y\cos(\pi x) \dfrac{dy}{dx}=0 \end{aligned}\] Now we evaluate at \((x, y)=\left(\dfrac{1}{4},\dfrac{1}{2}\right)\) and solve: \[\begin{aligned} \dfrac{\pi}{4}\cos\left(\dfrac{\pi}{2}\right)\dfrac{dy}{dx} +\sin\left(\dfrac{\pi}{2}\right) +\dfrac{\pi}{4}\sin\left(\dfrac{\pi}{4}\right) +\cos\left(\dfrac{\pi}{4}\right)\dfrac{dy}{dx}&=0 \\ 1 +\dfrac{\pi}{4}\dfrac{1}{\sqrt2} +\dfrac{1}{\sqrt2}\dfrac{dy}{dx}&=0 \end{aligned}\] \[\begin{aligned} f'\left(\dfrac{1}{4}\right) =\left.\dfrac{dy}{dx}\right|_{(\frac{1}{4},\frac{1}{2})} &=-\,\dfrac{1+\dfrac{\pi}{4}\dfrac{1}{\sqrt{2}}} {0+\dfrac{1}{\sqrt{2}}} \\ &=-\sqrt{2}-\dfrac{\pi}{4} \end{aligned}\] So the equation of the tangent line is: \[\begin{aligned} y&=f\left(\dfrac{1}{4}\right)+f'\left(\dfrac{1}{4}\right)\left(x-\dfrac{1}{4}\right) \\ &=\dfrac{1}{2}-\left(\sqrt{2}+\dfrac{\pi}{4}\right)\left(x-\dfrac{1}{4}\right) \\ &=-\left(\sqrt{2}+\dfrac{\pi}{4}\right)x+\dfrac{1}{2}+\dfrac{\sqrt{2}}{4}+\dfrac{\pi}{16} \end{aligned}\]
ad
Differentiate \(p(x)=\sin(\cos[\tan(\cot[\sec(\csc[x])])])\). This is a challenge problem, make sure to keep track of all the steps of the chain rule.
Apply the Chain Rule \(5\) times. Be careful with the last two steps.
\(\begin{aligned} p'(x)=&-\cos(\cos[\tan(\cot[\sec(\csc[x])])]) \\ &\cdot\sin[\tan(\cot[\sec(\csc[x])])] \\ &\cdot\sec^2(\cot[\sec(\csc[x])]) \\ &\cdot\csc^2[\sec(\csc[x])] \\ &\cdot\sec(\csc[x])\tan(\csc[x]) \\ &\cdot\csc[x]\cot[x] \\ \end{aligned}\)
Apply the Chain Rule \(5\) times: \[\begin{aligned} p'(x)= &\cos(\cos[\tan(\cot[\sec(\csc[x])])]) \\ &\cdot(-\sin[\tan(\cot[\sec(\csc[x])])]) \\ &\cdot\sec^2(\cot[\sec(\csc[x])]) \\ &\cdot(-\csc^2[\sec(\csc[x])]) \\ &\cdot\sec(\csc[x])\tan(\csc[x]) \\ &\cdot(-\csc[x]\cot[x]) \\ =&-\cos(\cos[\tan(\cot[\sec(\csc[x])])]) \\ &\cdot\sin[\tan(\cot[\sec(\csc[x])])] \\ &\cdot\sec^2(\cot[\sec(\csc[x])]) \\ &\cdot\csc^2[\sec(\csc[x])] \\ &\cdot\sec(\csc[x])\tan(\csc[x]) \\ &\cdot\csc[x]\cot[x] \end{aligned}\]
ls
The following problems require hyperbolic trig functions.
\(g(x)={\large e}^{\small\sinh x\cosh x}\)
\(\begin{aligned} g'(x)&={\large e}^{\small\sinh x\cosh x}(\sinh^2x + \cosh^2x) \\ &={\large e}^{\small\sinh x\cosh x}\cosh(2x) \end{aligned}\)
We use the Chain Rule and the Product Rule to differentiate the function: \[\begin{aligned} g'(x)&={\large e}^{\small\sinh x\cosh x}(\sinh x\sinh x + \cosh x\cosh x) \\ &={\large e}^{\small\sinh x\cosh x}(\sinh^2x + \cosh^2x) \\ &={\large e}^{\small\sinh x\cosh x}\cosh(2x) \end{aligned}\] where we simplified using the double angle identity \(\cosh(2x)=\cosh^2x + \sinh^2x\).
las
There is an alternate way to differentiate this function by using the double angle identity \(\sinh(2x)=2\sinh x\cosh x\) to first simplify the function to: \[ g(x)={\large e}^{\small\sinh x\cosh x}={\large e}^{\small\sinh(2x)/2} \] Then we differentiate: \[\begin{aligned} g'(x)&={\large e}^{\small\sinh(2x)/2}\;\dfrac{1}{2}[\cosh(2x)2] \\ &={\large e}^{\small\sinh x\cosh x}\cosh(2x) \end{aligned}\]
las
\(f(y)={\large e}^{\small2^{\small\cosh y}}\)
You'll need to use the Chain Rule twice and remember: \[ \dfrac{d}{dy}2^x=(\ln2) 2^x \]
\( f'(y)={\large e}^{\small2^{\small\cosh y}}(\ln2) 2^{\small\cosh y} \sinh y \)
We use the Chain Rule twice to differentiate the function: \[\begin{aligned} f'(y)&={\large e}^{\small2^{\small\cosh y}}\dfrac{d}{dy}\left(2^{\small\cosh y}\right) \\ &= {\large e}^{\small2^{\small\cosh y}}(\ln2) 2^{\small\cosh y} \dfrac{d}{dy}( \cosh y) \\ &= {\large e}^{\small2^{\small\cosh y}}(\ln2) 2^{\small\cosh y} \sinh y \end{aligned}\]
las
\(p(x)={\large e}^{\small\mathrm{csch}\,x\cosh^2 x} {\large e}^{\small-\mathrm{csch}\,x\sinh^2 x}\)
Remember the identity \(e^a e^b = e^{a + b}\).
\( p'(x)=-{\large e}^{\small\mathrm{csch}\,x} \mathrm{csch}\,x\mathrm{coth}\,x \)
First, we simplify the function using the identities \(e^a e^b = e^{a + b}\) and \(\cosh^2 x - \sinh^2 x=1\): \[\begin{aligned} p(x)&={\large e}^{\small\mathrm{csch}\,x\cosh^2 x-\mathrm{csch}\,x\sinh^2 x} \\ &={\large e}^{\small\mathrm{csch}\,x(\cosh^2 x - \sinh^2 x)} ={\large e}^{\small\mathrm{csch}\,x} \end{aligned}\] Then, we take the derivative using the Chain Rule: \[ p'(x)=-{\large e}^{\small\mathrm{csch}\,x} \mathrm{csch}\,x\,\mathrm{coth}\,x \]
las
×Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum
-