5. Vectors

d. Dot Product

7. Application - Work

In a mechanical system, the work done to move an object a distance \(D\) using a force \(F\) in the direction of motion is \[ W=FD \] Here \(D\) is the length of the displacement vector, \(\vec D\), and \(F\) is the magnitude of the force, \(\vec F\).

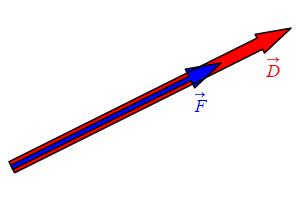
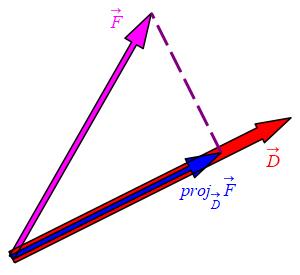
If the force, \(\vec F\), is not in the direction of motion, \(\vec D\), only the component (or scalar projection) in the direction of motion contributes to the work: \[ W=F_{\parallel}D \] where \[ F_{\parallel}=\text{comp}_{\vec D}\vec F =\dfrac{\vec F\cdot\vec D}{|\vec D|} \] Since \(D=|\vec D|\), the work is: \[ W=F_{\parallel}D=\dfrac{\vec F\cdot\vec D}{|\vec D|}|\vec D| =\vec F\cdot\vec D \] i.e. the dot product of the force and the displacement. You can compute the dot product using either the algebraic or the geometric formula.

A girl pulls a wagon \(5\) meters by applying a force of \(6\) Newtons at an angle of \(30^\circ\)above the horizontal. Find the work she does.

The displacement vector is \(5\) meters in the positive \(x\) direction. The force vector is \(6\) Newtons at \(\theta=30^\circ\) above horizontal. Therefore, we can find the work done on the wagon by computing the dot product \(W=\vec F\cdot\vec D\). Using the geometric formula, we find: \[\begin{aligned} W&=\vec F\cdot\vec D =|\vec F|\,|\vec D|\cos\theta \\ &=6\,\text{N}\cdot5\,\text{m}\cdot\cos30^\circ \\ &=30\cdot\dfrac{1}{2}\sqrt{3}\,\text{N-m} \\ &=15\sqrt{3}\,\text{J} \approx25.98\,\text{J} \end{aligned}\]

A \(30\) lb young boy slides down a sliding board from \((0,7)\) to \((8,1)\), measured in ft. So the force of gravity is \(\vec F_g=\left\langle 0,-30\right\rangle\) lb. At the same time, his father has his hand on his chest and slows him down with the force \(\vec F_\text{dad}=\langle-12,10\rangle\) lb. Find the work done by gravity and the total work done on the boy.

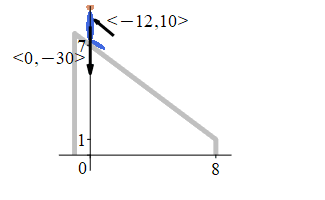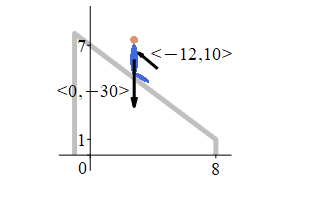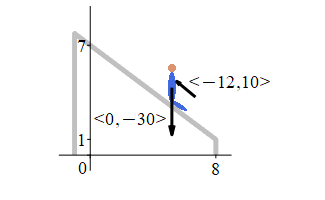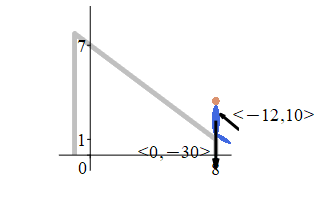
The work done by gravity is: \(W_g=180\,\text{ft-lb}\).
The total work is: \(W=24\,\text{ft-lb}\).

The total force is: \[\begin{aligned} \vec F&=\vec F_g+\vec F_\text{dad} =\left\langle0,-30\right\rangle+\left\langle -12,10\right\rangle \\ &=\left\langle-12,-20\right\rangle\,\text{lb} \end{aligned}\] The displacement is: \[ \vec D=(8,1)-(0,7)=\left\langle8,-6\right\rangle\,\text{ft} \] So the work done by gravity is: \[\begin{aligned} W_g&=\vec F_g\cdot\vec D =\left\langle 0,-30\right\rangle\cdot\left\langle 8,-6\right\rangle \\ &=180\,\text{ft-lb} \end{aligned}\] And the total work is: \[\begin{aligned} W&=\vec F\cdot\vec D =\left\langle -12,-20\right\rangle\cdot\left\langle 8,-6\right\rangle \\ &=-96+120=24\,\text{ft-lb} \end{aligned}\]

5. Vectors

d. Dot Product

7. Application - Work

Heading