5. Vectors

d. Dot Product

Recall the vector projections:

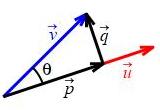
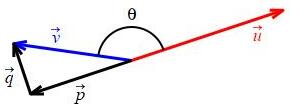
  def_ProjAcute   def_ProjObtuse
where   p⃗=proju⃗v⃗=v⃗⋅u⃗∣u⃗∣2u⃗\vec p=\text{proj}_{\vec u}\vec v=\dfrac{\vec v\cdot\vec u}{|\vec u|^2}\,\vec u   and   q⃗=proj⊥u⃗v⃗=v⃗−p⃗\vec q=\text{proj}_{\perp\vec u}\vec v=\vec v-\vec p.

6. Scalar Projections

It is sometimes also useful to define scalar projections (also called components) of v⃗\vec v parallel and perpendicular to u⃗\vec u. These are the lengths of the vector projections with the exception that for an obtuse angle the parallel component is the negative of the length so that the sign of the component tells whether the projection is in the same or opposite direction as u⃗\vec u. Thus:

Scalar Projections or Components
The component or scalar projection of the vector v⃗\vec v parallel to the direction of u⃗\vec u is denoted by compu⃗v⃗\text{comp}_{\vec u}\vec v while the component or scalar projection of the vector v⃗\vec v perpendicular to the direction of u⃗\vec u is denoted by comp⊥u⃗v⃗\text{comp}_{\perp\vec u}\vec v. compu⃗v⃗={∣proju⃗v⃗∣if θ is acute−∣proju⃗v⃗∣if θ is obtuse(*)comp⊥u⃗v⃗=∣proj⊥u⃗v⃗∣\begin{aligned} \text{comp}_{\vec u}\vec v &=\begin{cases} |\text{proj}_{\vec u}\vec v|&\text{if } \theta \text{ is acute} \\ -|\text{proj}_{\vec u}\vec v|&\text{if } \theta \text{ is obtuse} \qquad \text{(*)} \end{cases} \\ \text{comp}_{\perp\vec u}\vec v &=|\text{proj}_{\perp\vec u}\vec v| \end{aligned}

Again we would like to have computational fomulas for the components.

Parallel and Perpenducular Scalar Projections
The component or scalar projection of v⃗\vec v parallel to u⃗\vec u is compu⃗v⃗=∣v⃗∣cos⁡θ=v⃗⋅u⃗∣u⃗∣ \text{comp}_{\vec u}\vec v =|\vec v|\cos\theta =\dfrac{\vec v\cdot\vec u}{|\vec u|} The component or scalar projection of v⃗\vec v perpenducular to u⃗\vec u is comp⊥u⃗v⃗=∣v⃗∣sin⁡θ=∣v⃗∣2−(compu⃗v⃗)2 \text{comp}_{\perp\vec u}\vec v =|\vec v|\sin\theta =\sqrt{|\vec v|^2-\left(\text{comp}_{\vec u}\vec v\right)^2}

  def_ProjAcute   def_ProjObtuse
where   p⃗=proju⃗v⃗\vec p=\text{proj}_{\vec u}\vec v   and   q⃗=proj⊥u⃗v⃗\vec q=\text{proj}_{\perp\vec u}\vec v.  

From the diagram, we have: cos⁡θ={∣proju⃗v⃗∣∣v⃗∣if θ is acute−∣proju⃗v⃗∣∣v⃗∣if θ is obtuseandsin⁡θ=∣proj⊥u⃗v⃗∣∣v⃗∣ \cos\theta =\begin{cases} \dfrac{|\text{proj}_{\vec u}\vec v|}{|\vec v|}&\text{if } \theta \text{ is acute} \\ -\,\dfrac{|\text{proj}_{\vec u}\vec v|}{|\vec v|}&\text{if } \theta \text{ is obtuse} \end{cases} \qquad \text{and} \qquad \sin\theta=\dfrac{|\text{proj}_{\perp\vec u}\vec v|}{|\vec v|} since in the obtuse case the cos⁡θ\cos\theta needs to be negative. Solving for the magnitudes of the projections, we have: ∣proju⃗v⃗∣={∣v⃗∣cos⁡θif θ is acute−∣v⃗∣cos⁡θif θ is obtuseand∣proj⊥u⃗v⃗∣=∣v⃗∣sin⁡θ |\text{proj}_{\vec u}\vec v| =\begin{cases} |\vec v|\cos\theta&\text{if } \theta \text{ is acute} \\ -|\vec v|\cos\theta&\text{if } \theta \text{ is obtuse} \end{cases} \qquad \text{and} \qquad |\text{proj}_{\perp\vec u}\vec v|=|\vec v|\sin\theta Combining this with the definition (*) gives: compu⃗v⃗=∣v⃗∣cos⁡θandcomp⊥u⃗v⃗=∣v⃗∣sin⁡θ \text{comp}_{\vec u}\vec v=|\vec v|\cos\theta \qquad \text{and} \qquad \text{comp}_{\perp\vec u}\vec v=|\vec v|\sin\theta Notice that, in the obtuse case, the minus signs cancelled.

For the parallel component, we use the identity cos⁡θ=v⃗⋅u⃗∣v⃗∣∣u⃗∣\cos\theta=\dfrac{\vec v\cdot\vec u}{|\vec v|\,|\vec u|} to get: compu⃗v⃗=v⃗⋅u⃗∣u⃗∣ \text{comp}_{\vec u}\vec v=\dfrac{\vec v\cdot\vec u}{|\vec u|}

For the perpendicular component, we use the Pythagorean identity in the diagram above to get: comp⊥u⃗v⃗=∣v⃗∣2−(compu⃗v⃗)2 \text{comp}_{\perp\vec u}\vec v =\sqrt{|\vec v|^2-\left(\text{comp}_{\vec u}\vec v\right)^2}

[×]

Find the components of the vector w⃗=⟨−3,11⟩\vec w=\left\langle -3,11\right\rangle parallel and perpendicular to the vector v⃗=⟨1,3⟩\vec v=\left\langle 1,3\right\rangle. Is the angle between v⃗\vec v and w⃗\vec w acute or obtuse?

The parallel component is: compv⃗w⃗=w⃗⋅v⃗∣v⃗∣=⟨−3,11⟩⋅⟨1,3⟩∣⟨1,3⟩∣=3010=310\begin{aligned} \text{comp}_{\vec v}\vec w &=\dfrac{\vec w\cdot\vec v}{|\vec v|} =\dfrac{\left\langle -3,11\right\rangle\cdot\left\langle 1,3\right\rangle} {|\left\langle 1,3\right\rangle|} \\ &=\dfrac{30}{\sqrt{10}}=3\sqrt{10} \end{aligned} And the perpendicular component is: comp⊥v⃗w⃗=∣w⃗∣2−(compv⃗w⃗)2=9+121−90=40=210\begin{aligned} \text{comp}_{\perp\vec v}\vec w &=\sqrt{|\vec w|^2-\left(\text{comp}_{\vec v}\vec w\right)^2} \\ &=\sqrt{9+121-90}=\sqrt{40}=2\sqrt{10} \end{aligned} Since compv⃗w⃗=310>0\text{comp}_{\vec v}\vec w=3\sqrt{10} \gt 0, the angle is acute.

We check. From a example on the previous page, we have projv⃗w⃗=⟨3,9⟩andproj⊥v⃗w⃗=⟨−6,2⟩ \text{proj}_{\vec v}\vec w=\left\langle 3,9\right\rangle \qquad \text{and} \qquad \text{proj}_{\perp\vec v}\vec w=\left\langle -6,2\right\rangle So the components are: compv⃗w⃗=±∣projv⃗w⃗∣=±9+81=±90=310\begin{aligned} \text{comp}_{\vec v}\vec w&=\pm|\text{proj}_{\vec v}\vec w| \\ &=\pm\sqrt{9+81}=\pm\sqrt{90}=3\sqrt{10} \end{aligned} (We need the plus sign since the angle is acute.) comp⊥v⃗w⃗=∣proj⊥v⃗w⃗∣=36+4=40=210\begin{aligned} \text{comp}_{\perp\vec v}\vec w&=|\text{proj}_{\perp\vec v}\vec w| \\ &=\sqrt{36+4}=\sqrt{40}=2\sqrt{10} \end{aligned} Also notice ∣w⃗∣=32+112=130|\vec w|=\sqrt{3^2+11^2}=\sqrt{130} and (compv⃗w⃗)2+(comp⊥v⃗w⃗)2=902+402=130 \sqrt{(\text{comp}_{\vec v}\vec w)^2+(\text{comp}_{\perp\vec v}\vec w)^2} =\sqrt{\sqrt{90}^{\,2}+\sqrt{40}^{\,2}}=\sqrt{130}

Computing the length of the perpendicular projection is another good way to compute the perpendicular component. However, computing the length of the parallel projection will not tell you if the parallel component is positive or negative. For that, you must compute the dot product or use geometry to see if the angle is acute or obtuse.

Find the components of the vector a⃗=⟨7,−4⟩\vec a=\left\langle 7,-4\right\rangle parallel and perpendicular to the vector b⃗=⟨−1,2⟩\vec b=\left\langle -1,2\right\rangle. Is the angle between b⃗\vec b and a⃗\vec a acute or obtuse?

Answer

compb⃗a⃗=−35\text{comp}_{\vec b}\vec a=-3\sqrt{5}

comp⊥b⃗a⃗=25\text{comp}_{\perp\vec b}\vec a=2\sqrt{5}

The angle is obtuse.

[×]

Solution

The parallel component is: compb⃗a⃗=a⃗⋅b⃗∣b⃗∣=⟨7,−4⟩⋅⟨−1,2⟩∣⟨−1,2⟩∣=−155=−35\begin{aligned} \text{comp}_{\vec b}\vec a &=\dfrac{\vec a\cdot\vec b}{|\vec b|} =\dfrac{\left\langle 7,-4\right\rangle\cdot\left\langle -1,2\right\rangle} {|\left\langle -1,2\right\rangle|} \\ &=\dfrac{-15}{\sqrt{5}}=-3\sqrt{5} \end{aligned} And the perpendicular component is: comp⊥b⃗a⃗=∣a⃗∣2−(compb⃗a⃗)2=49+16−45=20=25\begin{aligned} \text{comp}_{\perp\vec b}\vec a &=\sqrt{|\vec a|^2-\left(\text{comp}_{\vec b}\vec a\right)^2} \\ &=\sqrt{49+16-45}=\sqrt{20}=2\sqrt{5} \end{aligned} Since compb⃗a⃗=−35<0\text{comp}_{\vec b}\vec a=-3\sqrt{5} \lt 0, the angle is obtuse.

[×]

Check

We check. From the exercise on the previous page, we have projb⃗a⃗=⟨3,−6⟩andproj⊥b⃗a⃗=⟨4,2⟩ \text{proj}_{\vec b}\vec a=\left\langle 3,-6\right\rangle \qquad \text{and} \qquad \text{proj}_{\perp\vec b}\vec a=\left\langle 4,2\right\rangle So the components are: compb⃗a⃗=±∣projb⃗a⃗∣=±9+36=±45=−35\begin{aligned} \text{comp}_{\vec b}\vec a&=\pm|\text{proj}_{\vec b}\vec a| \\ &=\pm\sqrt{9+36}=\pm\sqrt{45}=-3\sqrt{5} \end{aligned} (We need the minus sign since the angle is obtuse.) comp⊥b⃗a⃗=∣proj⊥b⃗a⃗∣=16+4=20=25\begin{aligned} \text{comp}_{\perp\vec b}\vec a&=|\text{proj}_{\perp\vec b}\vec a| \\ &=\sqrt{16+4}=\sqrt{20}=2\sqrt{5} \end{aligned}

[×]

© 2025 MYMathApps

Supported in part by NSF Grant #1123255