16. Max-Min Problems
b. Constrained Max-Min Problems
2. Lagrange Multiplier Method
The method of Lagrange multipliers is best explained by looking at a typical example. Suppose we want to maximize a function, \(f(x,y)\), along a constraint curve, \(g(x,y)=C\). In the plots at the right, the constraint, \(g(x,y)=C\), is shown in blue and the level curves of the extremal, \(f\), are shown in magenta. It is obvious from the \(1^\text{st}\) plot that the maximum value of \(f\) on the constraint is \(f=6\) which occurs at the point \(M\) where the level curve \(f=6\) is tangent to the constraint \(g=C\). If we were at any other point \(P\) where they are not tangent, then we could move in the direction toward bigger values of \(f\) until we reach \(M\).
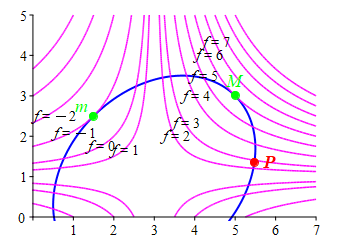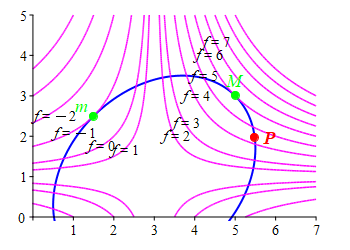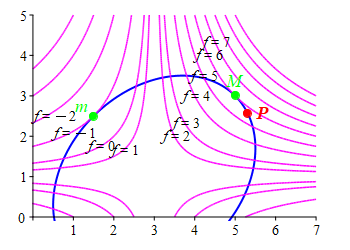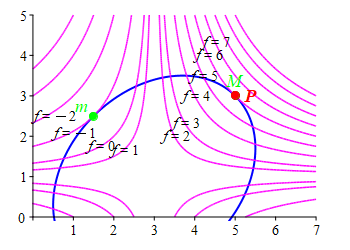
Similarly, the minimum \(f=-1\) occurs at the point \(m\) where the level curve \(f=-1\) is also tangent to the constraint \(g=C\). If we were at any other point \(P\) where they are not tangent, then we could move in the direction toward smaller values of \(f\) until we reach \(m\).
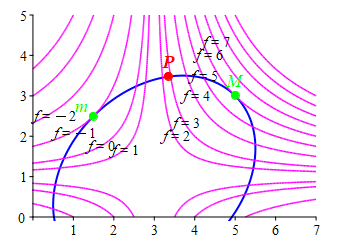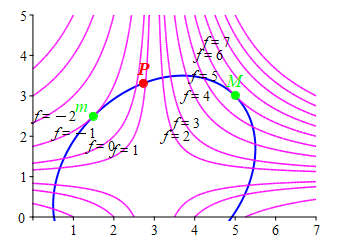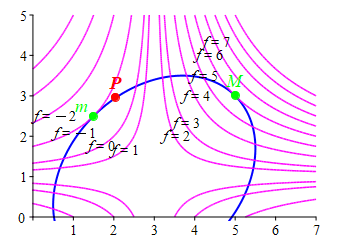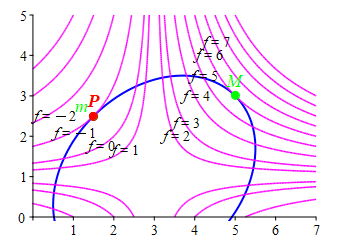
Since the maximum and minimum of a function \(f\) on a constraint \(g=C\) occur at points where the level curve of \(f\) is tangent to the constraint, which is itself a level curve of \(g\). Since the level curves are tangent, their normals are parallel. Further, the normals are the gradients of the functions \(f\) and \(g\). However, although the gradients \(\vec\nabla f\) and \(\vec\nabla g\) are parallel, their lengths can be different, i.e.: \[ \vec\nabla f=\lambda\vec\nabla g \] for some number \(\lambda\) (the Greek letter lambda) which is called the Lagrange multiplier. These equations are called the Lagrange equations. Since \(f\) and \(g\) are functions of \(2\) variables, there are \(2\) components in the gradients (the \(2\) partial derivatives) and so the Lagrange equations provide \(2\) equations for the \(3\) variables \(x\), \(y\) and \(\lambda\). We need one more equation. It is the constraint equation \(g=C\). So we solve the Lagrange equations together with the constraint for \(x\), \(y\) and \(\lambda\). Similar results hold for functions of more variables. (See below.)
Although in principal, we are solving for \(\lambda\). In fact, we don't really care about its value. It is merely a mathematical construct that helps us solve for the extrema.
Let's start with an example with only \(2\) variables which could be solved by the methods used in single-variable calculus, although with a lot more work.
Find the maximum and minimum values of the function \(f=x^2+y^2\) on the ellipse \(\dfrac{(x+y)^2}{16}+\dfrac{(x-y)^2}{9}=1\).
The extremal function is \(f=x^2+y^2\) and the constraint equation is \[ g=\dfrac{(x+y)^2}{16}+\dfrac{(x-y)^2}{9}=1 \] In the plot, the constraint is shown in blue and the level curves of the extremal are shown in magenta. From the plot, it is clear that the minimum and maximum are both between \(4\) and \(9\).
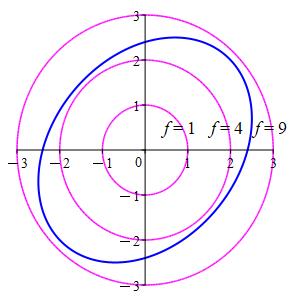
Since we are solving this equation using the Lagrange multiplier method, the first thing we need are the gradients of the two functions: \[\begin{aligned} \vec{\nabla}f&=\langle 2x,2y\rangle \\ \vec{\nabla}g&=\left\langle \dfrac{2(x+y) }{16}+\dfrac{2(x-y)}{9}, \dfrac{2(x+y) }{16}+\dfrac{-2(x-y) }{9}\right\rangle \end{aligned}\] We now insert these gradients into the Lagrange equations, \[ \vec{\nabla}f=\lambda\vec{\nabla}g \] The \(x\) and \(y\) components are: \[\begin{aligned} 2x&=\lambda \left(\dfrac{2(x+y)}{16}+\dfrac{2(x-y)}{9}\right) \qquad \text{(1)} \\ 2y&=\lambda \left(\dfrac{2(x+y)}{16}-\,\dfrac{2(x-y)}{9}\right) \qquad \text{(2)} \end{aligned}\] This is \(2\) equations, but there are \(3\) unknowns, \(x\), \(y\) and \(\lambda\). So we need a third equation. It is the constraint equation: \[ \dfrac{(x+y)^2}{16}+\dfrac{(x-y)^2}{9}=1 \qquad \text{(3)} \] To solve these, we divide equations (1) and (2) by \(2\) and then add and subtract them: \[\begin{aligned} x+y&=\lambda\dfrac{2(x+y)}{16} \qquad \text{(5)} \\ x-y&=\lambda\dfrac{2(x-y)}{9} \qquad \text{(6)} \end{aligned}\] We now rearrange (5) and (6) to factor out \(x+y\) and \(x-y\): \[\begin{aligned} (x+y)\left(1-\,\dfrac{\lambda}{8}\right)=0 \qquad \text{(7)} \\ (x-y)\left(1-\,\dfrac{2\lambda}{9}\right)=0 \qquad \text{(8)} \end{aligned}\] Equation (7) gives the cases \(x+y=0\) or \(\lambda=8\). Equation (8) gives the cases \(x-y=0\) or \(\lambda=\dfrac{9}{2}\). Together, these give only two cases:
-
Case 1: \(\lambda=\dfrac{9}{2}\) and \(x+y=0\):
With \(y=-x\), the constraint equation (3) gives: \[ (2x)^2=9 \qquad \text{or} \qquad x=\pm\dfrac{3}{2} \] So the critical points are \(\left(\dfrac{3}{2},-\,\dfrac{3}{2}\right)\) and \(\left(-\,\dfrac{3}{2},\dfrac{3}{2}\right)\). At both of these points the function value is: \[ f=x^2+y^2=\dfrac{9}{4}+\dfrac{9}{4}=\dfrac{9}{2} \] -
Case 2: \(\lambda=8\) and \(x-y=0\):
With \(y=x\), the constraint equation (3) gives: \[ (2x)^2=16 \qquad \text{or} \qquad x=\pm2 \] So the critical points are \((2,2)\) and \((-2,-2)\). At both of these points the function value is: \[ f=x^2+y^2=4+4=8 \]
So the maximum is \(f=8\) at \((2,2)\) and \((-2,-2)\) and the minimum is \(f=\dfrac{9}{2}\) at \(\left(\dfrac{3}{2},-\,\dfrac{3}{2}\right)\) and \(\left(-\,\dfrac{3}{2},\dfrac{3}{2}\right)\). Check these are reasonable in the plot. Notice that we don't care about the values of \(\lambda\).
Notice that in a problem like this we do not need to use the Second Derivative Test because we know we have found all the critical points. The one with the largest function value must be the maximum and the one with the smallest function value must be the minimum.
More Variables
The same works for any number of variables. The maximum and minimum of a function \(f\) on a constraint \(g=C\) occur at points where the level set (surface or higher dimensional surface) of \(f\) is tangent to the constraint, which is a level set of \(g\). Since the level sets are tangent, their normals are parallel. Further, the normals are the gradients of the functions \(f\) and \(g\). Once again, although the gradients \(\vec\nabla f\) and \(\vec\nabla g\) are parallel, their lengths can be different, i.e.: \[ \vec\nabla f=\lambda\vec\nabla g \] for some Lagrange multiplier \(\lambda\). If \(f\) and \(g\) are functions of \(n\) variables, namely \(x_1, x_2, \cdots, x_n\), then there are \(n\) components in the gradients (the \(n\) partial derivatives) and so the Lagrange equations provide \(n\) equations for the \(n+1\) unknowns \(x_1, x_2, \cdots, x_n\) and the Lagrange multiplier \(\lambda\). We need one more equation. It is the constraint equation \(g=C\). We solve the Lagrange equations together with the constraint. Once again, we don't really care about the value of \(\lambda\). It is merely a mathematical construct that helps us solve for the extrema.
We now redo an exercise from the previous page which was difficult because the derivatives involved square roots. The Lagrange multiplier method avoids the square roots.
Find the dimensions and volume of the largest rectangular box inscribed in the ellipsoid \(x^2+\dfrac{y^2}{4}+\dfrac{z^2}{16}=1\).
Note: "Inscribed" means all \(8\) vertices lie on the ellipsoid. What are the length, width and height?
The length, width and height are: \[ L=\dfrac{2}{\sqrt{3}} \qquad W=\dfrac{4}{\sqrt{3}} \qquad H=\dfrac{8}{\sqrt{3}} \] So the volume is: \[ V=\dfrac{64}{3\sqrt{3}} \]
The extremal is the volume:
\[
V=LWH=(2x)(2y)(2z)=8xyz
\]
and the constraint is the equation of the ellipsoid:
\[
g=x^2+\dfrac{y^2}{4}+\dfrac{z^2}{16}=1
\]
We compute their gradients:
\[\begin{aligned}
\vec{\nabla}V&=\langle 8yz,8xz,8xy\rangle \\
\vec{\nabla}g&=\left\langle 2x,\dfrac{y}{2},\dfrac{z}{8}\right\rangle
\end{aligned}\]
The Lagrange equations, \(\vec\nabla V=\lambda\vec\nabla g\) are:
\[\begin{aligned}
8yz&=\lambda 2x \qquad \text{(1)} \\
8xz&=\lambda \dfrac{y}{2} \qquad \text{(2)} \\
8xy&=\lambda \dfrac{z}{8} \qquad \text{(3)}
\end{aligned}\]
We need to solve these \(3\) equations and the constraint for \(x\), \(y\),
\(z\) and \(\lambda\). A frequently used trick is to multiply
the first equation by \(x\), the second by \(y\) and the third
by \(z\) making the left sides all equal. We can then equate them and get
the \(\lambda\) to cancel out:
\[
8xyz=\lambda 2x^2=\lambda \dfrac{y^2}{2}=\lambda \dfrac{z^2}{8}
\]
The \(x\) and \(y\) pieces say \(y^2=4x^2\) or \(y=2x\).
The \(x\) and \(z\) pieces say \(z^2=16x^2\) or \(z=4x\).
Substituting these into the constraint gives:
\[
g=x^2+\dfrac{4x^2}{4}+\dfrac{16x^2}{16}=3x^2=1
\]
Consequently,
\[
x=\dfrac{1}{\sqrt{3}} \qquad y=\dfrac{2}{\sqrt{3}} \qquad z=\dfrac{4}{\sqrt{3}}
\]
So, the length, width and height are:
\[
L=2x=\dfrac{2}{\sqrt{3}} \qquad W=2y=\dfrac{4}{\sqrt{3}} \qquad H=2z=\dfrac{8}{\sqrt{3}}
\]
and the volume is:
\[
V=LWH=\dfrac{64}{3\sqrt{3}}
\]
From this exercise, you should notice that the Lagrange multiplier method is much easier than eliminating a variable, about half as much work.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum