16. Max-Min Problems

b. Constrained Max-Min Problems

This topic is optional. It uses parametric curves and parametric surfaces which were introduced in the chapter on Curves and Surfaces
Parametric curves were discussed in more detail in the chapter on Properties of Curves
Parametric surfaces will be discussed in more detail in the chapter on Parametric Surfaces and Surface Integrals
It may be better to delay this topic until after parametric surfaces.

3. Parametrization Method (Optional)

We can also optimize a function that is constrained on a curve (or surface) by parametrizing the curve (or surface). The first step is to write out the parametrization. Plugging the parametrization into the extremal function reduces the number of variables to \(1\) for curves and \(2\) for surfaces.

First we look at a problem which is constrained to a curve.

Find the maximum and minimum values of the function \(f=3x+y+3z\) on the ellipse which is the intersection of the plane \(x=y\) and the cylinder \(x^2+z^2=1\). This ellipse may be parametrized by \(\vec r(\theta)=(\cos\theta,\cos\theta,\sin\theta)\).
PY: Add a plot

We substitute the curve into the extremal: \[ f=3x+y+3z=3\cos\theta+\cos\theta+3\sin\theta=4\cos\theta+3\sin\theta \]

We differentiate and set this equal to zero: \[ f_\theta=-4\sin\theta+3\cos\theta=0 \] This says \(\tan\theta=\dfrac{3}{4}\). There are two angles that satisfy this: \(\theta_1\) in the first quadrant and \(\theta_2\) in the third quadrant. If you draw a right triangle with opposite side \(3\) and adjacent side \(4\), then the tangent is \(\dfrac{3}{4}\). The same ratio occurs in the third quadrant. Further, the hypotenuse is \(5\). Consequently, the two solutions satisfy:

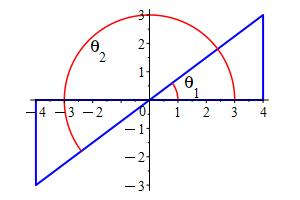
eg_345tri

\[ \sin\theta_1=\dfrac{3}{5} \qquad \text{and} \qquad \cos\theta_1=\dfrac{4}{5} \] and \[ \sin\theta_2=\dfrac{-3}{5} \qquad \text{and} \qquad \cos\theta_2=\dfrac{-4}{5} \] So the two points are \[ r(\theta_1)=\left(\dfrac{4}{5},\dfrac{4}{5},\dfrac{3}{5}\right) \qquad \text{and} \qquad r(\theta_2)=\left(\dfrac{-4}{5},\dfrac{-4}{5},\dfrac{-3}{5}\right) \] The values of the function \(f=3x+y+3z\) are \[ f\left(\dfrac{4}{5},\dfrac{4}{5},\dfrac{3}{5}\right) =3\cdot\dfrac{4}{5}+\dfrac{4}{5}+3\cdot\dfrac{3}{5}=5 \] and \[ f\left(\dfrac{-4}{5},\dfrac{-4}{5},\dfrac{-3}{5}\right) =3\cdot\dfrac{-4}{5}+\dfrac{-4}{5}+3\cdot\dfrac{-3}{5}=-5 \] So the maximum is \(5\) and the minimum is \(-5\).

We now look at an example where the constraint is a surface.

Find the maximum value of the function \(f=8x+6y+z\) on the paraboloid \(z=30-x^2-y^2\)

First we can parametrize the surface as \[ (x,y,z)=\vec R(r,\theta)=(r\cos\theta,r\sin\theta,30-r^2) \] Substituting this into the function gives \[ f=8r\cos\theta+6r\sin\theta+(30-r^2) \] We set the partial derivatives equal to \(0\): \[\begin{aligned} \dfrac{\partial f}{\partial r} &=8\cos\theta+6\sin\theta-2r=0 \qquad \text{(1)} \\ \dfrac{\partial f}{\partial \theta} &=-8r\sin\theta+6r\cos\theta=0 \qquad \text{(2)} \end{aligned}\] The equation (2) says either \(r=0\) or \(\tan\theta=\dfrac{6}{8}=\dfrac{3}{4}\).

Finally, we redo an exercise which was done twice previously, once by eliminating the constraint and once by Lagrange multipliers. That way we can see the difference in the three methods.

Find the dimensions and volume of the largest rectangular box inscribed in the ellipsoid \(x^2+\dfrac{y^2}{4}+\dfrac{z^2}{16}=1\).

The ellipsoid may be parametrized using elliptic coordinates given by: \[\begin{aligned} x&=\sin(\phi)\cos(\theta) \\ y&=2\sin(\phi)\sin(\theta) \\ z&=4\cos(\phi) \end{aligned}\] These generalize spherical coordinates but have a different radius in each direction.

The length, width and height are: \[ L=\dfrac{2}{\sqrt{3}} \qquad W=\dfrac{4}{\sqrt{3}} \qquad H=\dfrac{8}{\sqrt{3}} \] So the volume is: \[ V=\dfrac{64}{3\sqrt{3}} \]

The ellipsoid may be parametrized using elliptic coordinates given by: \[\begin{aligned} x&=\sin(\phi)\cos(\theta) \\ y&=2\sin(\phi)\sin(\theta) \\ z&=4\cos(\phi) \end{aligned}\] These generalize spherical coordinates but have a different radius in each direction. We substitute these into the formula for the volume. \[ V=LWH=(2x)(2y)(2z)=8xyz=64\sin^2(\phi)\cos(\phi)\sin(\theta)\cos(\theta) \] We find the partial derivatives and set them equal to \(0\): \[\begin{aligned} \dfrac{\partial V}{\partial\phi} &=\left(128\sin(\phi)\cos^2(\phi)-64\sin^3(\phi)\right)\sin(\theta)\cos(\theta)=0 \\ \dfrac{\partial V}{\partial\theta} &=64\sin^2(\phi)\cos(\phi)\left(\cos^2(\theta)-\sin^2(\theta)\right)=0 \\ \end{aligned}\] Now, the maximum volume cannot be \(0\). So \(x\), \(y\) and \(z\) cannot be \(0\). So \(\sin(\phi)\), \(\cos(\phi)\), \(\sin(\theta)\) and \(\cos(\theta)\) cannot be \(0\). So the partial derivative equations reduce to: \[\begin{aligned} &2\cos^2(\phi)-\sin^2(\phi)=0 \\ &\cos^2(\theta)-\sin^2(\theta)=0 \\ \end{aligned}\] In other words, \(\tan(\phi)=\sqrt{2}\) and \(\tan(\theta)=1\). The condition on \(\theta\) says \(\theta=\dfrac{\pi}{4}\). So: \[ \sin(\theta)=\cos(\theta)=\dfrac{1}{\sqrt{2}} \]

To understand the condition on \(\phi\), think of a right triangle with sides \(1\) and \(\sqrt{2}\) and hypotenuse \(\sqrt{3}\). Then: \[ \sin(\phi)=\dfrac{\sqrt{2}}{\sqrt{3}} \qquad \text{and} \qquad \cos(\phi)=\dfrac{1}{\sqrt{3}} \]
PY: Add plot.

ex_1s2s3tri

Consequently: \[\begin{aligned} x&=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{\sqrt{2}} =\dfrac{1}{\sqrt{3}} \\ y&=2\cdot\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{\sqrt{2}} =\dfrac{2}{\sqrt{3}} \\ z&=4\cdot\dfrac{1}{\sqrt{3}}=\dfrac{4}{\sqrt{3}} \end{aligned}\] So, the length, width and height are: \[ L=2x=\dfrac{2}{\sqrt{3}} \qquad W=2y=\dfrac{4}{\sqrt{3}} \qquad H=2z=\dfrac{8}{\sqrt{3}} \] and the volume is: \[ V=LWH=\dfrac{64}{3\sqrt{3}} \]

Comparing the three methods of solving this problem, Lagrange multipliers is probably easiest, then parametrizing the surface (We need to parametrize the surface.) and finally eliminating a variable (We need to deal with ugly square roots.).

© MYMathApps

Supported in part by NSF Grant #1123255