14. Directional Derivatives and Gradients
d. Properties of the Gradient
While discussing the derivative along a curve, we introduced the gradient of a function, which is the vector field of all partial derivatives of the function: \[ \text{grad}\,f=\vec\nabla f =\left\langle\dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z}\right\rangle \]
1. Proposition
The gradient satisfies four properties (one of which is only qualitative):
- \(\vec\nabla f\) points in the direction of maximum increase of \(f\).
- \(|\vec\nabla f|\) is the maximum rate of increase of \(f\).
- \(\vec\nabla f\) points perpendicular to each level set of \(f\).
- \(|\vec\nabla f|\) is inversely proportional to the spacing between level sets. (Qualitative)
The proofs are straight forward and informative. You should read them.
Proof of Gradient Properties 1 and 2
For property 1, we need to show \(\vec\nabla f\) points in the same direction as the unit vector \(\hat v\) for which the directional derivative \(\nabla_{\hat v}f\) is largest.
We use the directional derivative rather than the derivative along a general vector \(\vec v\) for two reasons. First, we want to measure the intrinsic change in \(f\), independent of the speed of the observer doing the measuring. And second, \(\nabla_{\vec v}f=\vec v\cdot\vec\nabla f\) can be made arbitrarily large by making \(|\vec v|\) bigger; so there would be no maximum of \(\nabla_{\vec v}f\).
From the definition of a directional derivative, we have \[ \nabla_{\hat v}f=\hat v\cdot\vec\nabla f \] In the figure at the right, \(\vec\nabla f\) is a fixed vector, while \(\hat v\) is a unit vector whose direction varies until \(\hat v\cdot\vec\nabla f\) is a maximum.
Using the geometrical formula for the dot product ( \(\vec u\cdot\vec v=|\vec u|\,|\vec v|\cos\theta\) ) and the fact that \(\hat v\) is a unit vector ( \(|\hat v|=1\) ), the directional derivative becomes: \[ \nabla_{\hat v}f=|\hat v|\,|\vec\nabla f|\cos\theta =|\vec\nabla f|\cos\theta \] where \(\theta\) is the angle between \(\hat v\) and \(\vec\nabla f\). Since \(|\vec\nabla f|\) is constant, this is a maximum when \(\cos\theta=1\) or \(\theta=0\). So the maximum occurs when \(\hat v\) is parallel to \(\vec\nabla f\). In other words, \(\vec\nabla f\) points in the direction \(\hat v\) in which \(\nabla_{\hat v}f\) is a maximum. This proves property 1.
In addition, if \(\theta=0\) then \(\cos\theta=1\) and the directional derivative becomes \[ \nabla_{\hat v}f=|\vec\nabla f| \] In other words, the maximum rate of change of \(f\) is \(|\vec\nabla f|\). This proves property 2.
Proof of Gradient Properties 3 and 4
2D Diagrams
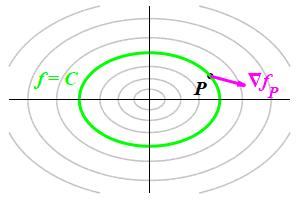
Consider a level set of a function \(f\) shown in 2D on the left
and 3D on the right. Let \(P\) be a point on the level set with value
\(f=C\), i.e.:
\[
f(P)=C
\]
and let \(\left.\vec\nabla f\right|_P\) be the gradient of \(f\) at \(P\).
Note: \(\left.\vec\nabla f\right|_P\) is not drawn perpendicular to the
level set, since that is what we need to prove.
3D Diagrams
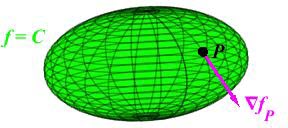
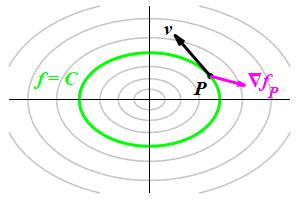
Now let \(\vec v\) be a vector tangent to the level set \(f=C\) at the point \(P\). We need to show that \(\left.\vec\nabla f\right|_P\) is perpendicular to every such \(\vec v\).
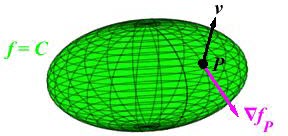
To show this, let \(\vec r(t)\) be a parametric curve which lies in the level set \(f=C\) and has tangent vector \(\vec v\) at \(P\), i.e.: \[ f(\vec r(t))=C \quad \text{and} \quad \left.\dfrac{d\vec r}{dt}\right|_P=\vec v \]
We now compute \(\dfrac{d(f\circ \vec r)}{dt}\) in two ways: On the one hand, this is the derivative of \(f\) along the curve. So \[ \dfrac{d(f\circ \vec r)}{dt}=\dfrac{df}{dt}=\vec v\cdot\vec\nabla f \] On the other hand, since the curve lies on the level set, \(f(\vec r(t))\) has the constant value \(C\). So \[ \dfrac{d(f\circ \vec r)}{dt}=\dfrac{df(\vec r(t))}{dt}=\dfrac{dC}{dt}=0 \] Together, these say \[ \vec v\cdot\vec\nabla f=0 \] which says \(\vec\nabla f\) is perpendicular to \(\vec v\). This proves property 3.
Property 4 is only qualitative. Think of the contour plot at the right as a contour map of the altitude of the land above sea level. When the contours are closer together, the altitude, \(f\), is changing quickly and so the \(|\vec\nabla f|\) is large. Conversely, when the contours are farther apart, the altitude, \(f\), is changing slowly and so the \(|\vec\nabla f|\) is small. This is what is meant by property 4.
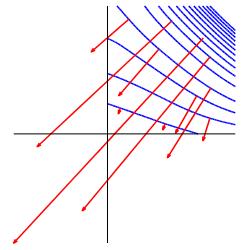
Notice there are two properties about the direction of \(\vec\nabla f\) and two properties about the magnitude of \(\vec\nabla f\). Further there are two properties about the maximum increase of \(f\) and two properties about the level sets of \(f\).
Applications are on the next two pages.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum