20. Convergence of Positive Series

g. Approximating the Series

2. Improved Integral Bounds

Assume \(a_n=f(n)\) where \(f(x)\) is a continuous, positive, decreasing function on \(\lbrack n_o,\infty)\) and \(\displaystyle \int_{n_o}^\infty f(x)\,dx\) is convergent. When the series \(\displaystyle S=\sum_{n=n_o}^\infty a_n\) is approximated by the partial sum \(\displaystyle S_k=\sum_{n=n_o}^k a_n\), the integral \(\displaystyle \int_k^\infty f(x)\,dx\) is an upper bound on the error \(E_k=S-S_k\). However, the approximation to the series can be improved and the error estimate can be vastly reduced if we also use an integral which is a lower bound on the error.

In a previous example, we approximated the series \(\displaystyle S=\sum_{n=1}^\infty \dfrac{1}{n^2}\) by the \(10^\text{th}\) partial sum \(\displaystyle S_{10}=\sum_{n=1}^{10} \dfrac{1}{n^2}\approx 1.5498\) and showed the error \(\displaystyle E_{10}=S-S_{10}=\sum_{n=11}^\infty \dfrac{1}{n^2}\) is less than the integral bound \(\displaystyle \int_{10}^\infty \dfrac{1}{n^2}\,dn=.1\). Improve the approximation by using upper and lower integral bounds on the error \(E_{10}\).

Recall the Derivation of the Integral Test. It can be used to produce both upper and lower bounds on the error, as follows:

In the figure at the right, the area under the blue curve is \(\displaystyle \int_{10}^\infty \dfrac{1}{n^2}\,dn\) while the area under the red rectangles is \(\displaystyle \sum_{n=11}^\infty \dfrac{1}{n^2}\). Thus the integral,

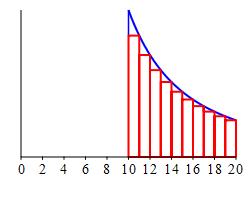
eg_integ_err_upper

\[ U=\int_{10}^\infty \dfrac{1}{n^2}\,dn=\left[\dfrac{-1}{n}\right]_{10}^\infty =[0] -\left[-\dfrac{1}{10}\right]=\dfrac{1}{10} \] is an upper bound on the error \(\displaystyle E_{10}=\sum_{n=11}^\infty \dfrac{1}{n^2}\).

Similarly, in the figure at the right, the area under the blue curve is \(\displaystyle \int_{11}^\infty \dfrac{1}{n^2}\,dn\) while the area under the red rectangles is \(\displaystyle \sum_{n=11}^\infty \dfrac{1}{n^2}\). Thus the integral,

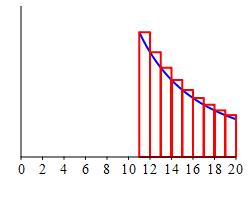
eg_integ_err_lower

\[ L=\int_{11}^\infty \dfrac{1}{n^2}\,dn=\left[\dfrac{-1}{n}\right]_{11}^\infty =[0] -\left[-\dfrac{1}{11}\right]=\dfrac{1}{11} \] is an lower bound on the error \(\displaystyle E_{10}=\sum_{n=11}^\infty \dfrac{1}{n^2}\).

Thus the error is bounded by: \[ L \lt E_{10} \lt U \] Since the sum of the series is \(S=S_{10}+E_{10}\), we add \(S_{10}\) to this inequality to get lower and upper bounds on the sum: \[ S_{10}+L \lt S \lt S_{10}+U \] So a better estimate for the sum is the midpoint of the interval \([S_{10}+L,S_{10}+U]\): \[ S\approx\overline{S_{10}}\equiv S_{10}+\dfrac{U+L}{2} \] In this problem \[ \sum_{n=1}^\infty \dfrac{1}{n^2} \approx\overline{S_{10}} =1.5498+\dfrac{\dfrac{1}{10}+\dfrac{1}{11}}{2}=1.6452 \] The error in this approximation is less than half of the width of the interval \([S_{10}+L,S_{10}+U]\): \[ \overline{E_{10}}\equiv S-\overline{S_k} \lt \dfrac{U-L}{2} \] In this problem \[ \overline{E_{10}} \lt \dfrac{\dfrac{1}{10}-\dfrac{1}{11}}{2}\approx.0046 \] Notice, we have reduced the error from \(U=0.1\) to \(\dfrac{U-L}{2}=.0046\).

To summarize (and generalize) these results, we have

Assume \(a_n=f(n)\) where \(f(x)\) is a continuous, positive, decreasing function on \([n_o,\infty)\) and \(\displaystyle \int_{n_o}^\infty f(x)\,dx\) is convergent. In other words, \(\displaystyle S=\sum_{n=n_o}^\infty a_n\) converges by the Integral Test.

For \(k \gt n_o\), let \(\displaystyle U_k=\int_k^\infty f(x)\,dx\) and \(\displaystyle L_k=\int_{k+1}^\infty f(x)\,dx\).

  1. If the series \(\displaystyle S=\sum_{n=n_o}^\infty a_n\) is approximated by \(\displaystyle S_k=\sum_{n=n_o}^k a_n\), then the error in the approximation, \(\displaystyle E_k=S-S_k=\sum_{n=k+1}^\infty a_n\), is less than \(U_k\).
  2. If the series \(\displaystyle S=\sum_{n=n_o}^\infty a_n\) is approximated by \(\overline{S_k}=S_k+\dfrac{U_k+L_k}{2}\), then the error in the approximation, \(\displaystyle \overline{E_k}=S-\overline{S_k}\), is less than \(\begin{aligned} \displaystyle \dfrac{U_k-L_k}{2}=\int_k^{k+1} f(x)\,dx \end{aligned}\).

In a previous exercise, we approximated the series \(\displaystyle S=\sum_{n=1}^\infty \dfrac{1}{n^2+1}\) by the \(100^\text{th}\) partial sum \(\displaystyle S_{100}=\sum_{n=1}^{100} \dfrac{1}{n^2+1}\approx 1.066\,724\) and showed the error \(\displaystyle E_{100}=S-S_{100} =\sum_{n=101}^\infty \dfrac{1}{n^2+1}\) is less than the integral bound \(\displaystyle \int_{100}^\infty \dfrac{1}{n^2+1}\,dn\approx .01\). Improve the approximation by using upper and lower integral bounds on the error \(E_{100}\).

The improved approximation is \(\overline{S_{100}}=1.076\,674\)
and the error is \(\overline{E_{100}} \lt 4.95\times10^{-5}\).

The upper bound on the error \(E_{100}\) is \[\begin{aligned} U&=\int_{100}^\infty \dfrac{1}{n^2+1}\,dn=\left.\arctan n\right|_{100}^\infty \\ &=\dfrac{\pi}{2}-\arctan 100\approx 9.9997\times10^{-3} \end{aligned}\] The lower bound on the error \(E_{100}\) is \[\begin{aligned} L&=\int_{101}^\infty \dfrac{1}{n^2+1}\,dn=\left.\arctan n\right|_{101}^\infty \\ &=\dfrac{\pi}{2}-\arctan 101\approx 9.9007\times10^{-3} \end{aligned}\] The improved approximation is \[\begin{aligned} \overline{S_{100}}&=S_{100}+\dfrac{U+L}{2} \\ &=1.066\,724+\dfrac{9.9997\times10^{-3}+9.9007\times10^{-3}}{2} \\ &=1.076\,674 \end{aligned}\] and the error in the improved approximation is \[\begin{aligned} \overline{E_{100}} &\lt \dfrac{U-L}{2} \\ &=\dfrac{9.9997\times10^{-3}-9.9007\times10^{-3}}{2} =4.95\times10^{-5} \end{aligned}\] We have reduced the error from \(U=0.01\) to \(\dfrac{U-L}{2}=4.95\times10^{-5}\).

© MYMathApps

Supported in part by NSF Grant #1123255