18. Sequences
Sometimes we are unable to compute a limit exactly. However, if we can at least show that the limit exists, then we can use some numerical technique to approximate the limit. We now introduce two properties of sequences (bounded and monotonic) which together help us show the limit exists.
c1. Bounded Sequences
A sequence \(a_n\) is
bounded above
if there is a number \(M\) such that \(a_n \le M\) for all \(n\).
Then \(M\) is called an upper bound.
A sequence \(a_n\) is
bounded below
if there is a number \(m\) such that \(a_n \ge m\) for all \(n\).
Then \(m\) is called an lower bound.
A sequence \(a_n\) is
bounded if it is both bounded above and
bounded below.
Here are some examples:
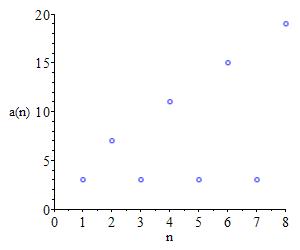
Bounded above by \(3\).
Unbounded below.
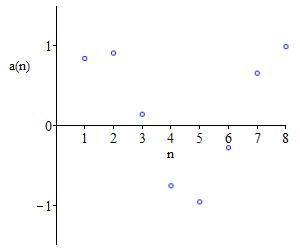
Bounded above by \(1\).
Bounded below by \(-1\).
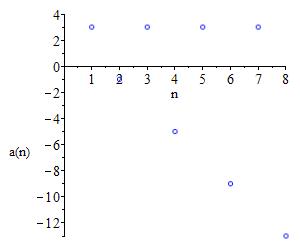
Bounded below by \(3\).
Unbounded above.
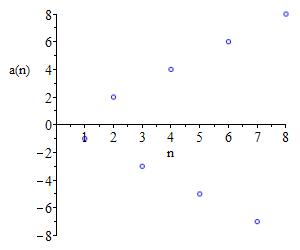
Unbounded above.
Unbounded below.
Determine if each sequence is bounded above, below, neither or both. When appropriate, find upper and lower bounds.
-
\(a_n=2-\dfrac{1}{n}\)
Bounded below by \(1\) and bounded above by \(2\).
Since \(n \ge 1,\) then \(0<\dfrac{1}{n}\le1\) and \(0>-\dfrac{1}{n}\ge-1\) and \(2>2-\dfrac{1}{n}\ge1\).
So \(\left\{ 2-\dfrac{1}{n}\right\}\) is bounded below by \(1\) and bounded above by \(2\). -
\(a_n=(-1)^n n-n\)
Bounded above by \(0\) but not bounded below.
We study the sequence \(a_n=(-1)^n n-n\) separately for \(n\) odd and \(n\) even.
For \(n\) odd, \((-1)^n=-1\) and \(a_n=-2n\) which is always negative and becomes arbitrarily large and negative.
For \(n\) even, \((-1)^n=1\) and \(a_n=n-n=0\).
So the sequence is bounded above by \(0\) (or by any positive number) but the sequence is not bounded below and so is not bounded. -
\(a_n=\dfrac{n!}{2^n}\)
Bounded below by \(0\) (or \(\dfrac{1}{2}\)) but unbounded above.
Since the terms \(a_n=\dfrac{n!}{2^n}\) are all positive, the sequence is bounded below by \(0\).
To see if there is an upper bound, we write the \(n^\text{th}\) term as: \[ a_n=\dfrac{1}{2}\cdot\dfrac{2}{2}\cdot\dfrac{3}{2}\cdot\dfrac{4}{2} \cdot\,\cdots\,\cdot\dfrac{n-1}{2}\cdot\dfrac{n}{2} =a_{n-1}\cdot\dfrac{n}{2} \] Thus as long as \(n \gt 2\), the term \(a_n\) is the term \(a_{n-1}\) times something bigger than \(1\), namely \(\dfrac{n}{2}\). So we suspect the sequence is unbounded above.
To see this we use a proof by contradiction. Suppose there is an upper bound \(M\). Then the term \(a_{4M}\) is \[\begin{aligned} a_{4M} &=\dfrac{1}{2}\cdot\dfrac{2}{2}\cdot\dfrac{3}{2}\cdot \dfrac{4}{2}\cdot\,\cdots\,\cdot \dfrac{4M-1}{2}\cdot\dfrac{4M}{2} \\ &=M\cdot\dfrac{2}{2}\cdot\dfrac{3}{2}\cdot \dfrac{4}{2}\cdot\,\cdots\,\cdot \dfrac{4M-1}{2} \end{aligned}\] which is \(M\) times a number bigger than \(1\). So \(a_{4M} \gt M\) which contradicts the assumption that \(M\) is an upper bound.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum