7. Trigonometric Substitutions

a1. Substitutions for \(x^2+1\) - Tangent Substitutions

Recall the derivative and integral formulas for \(\arctan x\): \[ \dfrac{d}{dx}\arctan x=\dfrac{1}{x^2+1} \qquad \qquad \qquad \int \dfrac{1}{x^2+1}\,dx=\arctan x+C \] and the second Pythagorean Trig Identity: \[ \tan^2\theta+1=\sec^2\theta \]

These formulas motivate the following integration technique:

If the integrand involves the quantity \(x^2+1\) then it may be useful to make the substitution \(x=\tan\theta\). Then \(dx=\sec^2\theta\,d\theta\) and \(x^2+1=\tan^2\theta+1=\sec^2\theta\). So it may be possible to re-express the integrand in terms of \(\tan\theta\) and \(\sec\theta\) only.

Here are some examples:

Compute \(\displaystyle \int \dfrac{1}{\sqrt{x^2+1}}\,dx\).

We substitute \(x=\tan\theta\). Then \(dx=\sec^2\theta\,d\theta\) and so \[\begin{aligned} \int \dfrac{1}{\sqrt{x^2+1}}\,dx &=\int \dfrac{1}{\sqrt{\tan^2\theta+1}}\,\sec^2\theta\,d\theta \\ &=\int \dfrac{1}{\sqrt{\sec^2\theta}}\,\sec^2\theta\,d\theta =\int \sec\theta\,d\theta \\ &=\ln|\sec\theta+\tan\theta|+C \end{aligned}\] Don't forget to substitute for the differential! Don't forget to substitute back! We already know that \(\tan\theta=x\) from the definition of the substitution. We also need a formula for \(\sec\theta\) in terms of \(x\). There are two ways to find this formula:

We can use the Pythagorean identity \(\tan^2\theta+1=\sec^2\theta\). Then: \[ \sec\theta=\sqrt{\tan^2\theta+1}=\sqrt{x^2+1} \]

We can draw a right triangle with an angle \(\theta\) whose opposite side is \(x\) and whose adjacent is \(1\). These sides are chosen so that \(\tan\theta=\dfrac{x}{1}=x\). Then the hypotenuse is \(\sqrt{x^2+1}\) and so: \[ \sec\theta=\dfrac{\text{HYP}}{\text{ADJ}} =\dfrac{\sqrt{x^2+1}}{1}=\sqrt{x^2+1} \]

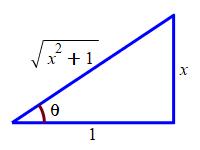
Returning to the problem at hand, we conclude: \[ \int \dfrac{1}{\sqrt{x^2+1}}\,dx =\ln\left|\sqrt{x^2+1}+x\right|+C \]

We check by differentiating. If \(f(x)=\ln\left|\sqrt{x^2+1}+x\right|\) then \[\begin{aligned} f'(x) &=\dfrac{1}{\sqrt{x^2+1}+x}\left(\dfrac{1}{2}\dfrac{2x}{\sqrt{x^2+1}}+1\right) \\ &=\dfrac{1}{\sqrt{x^2+1}+x}\left(\dfrac{x+\sqrt{x^2+1}}{\sqrt{x^2+1}}\right) =\dfrac{1}{\sqrt{x^2+1}} \end{aligned}\] which is the integrand we started with.

Compute \(\displaystyle \int \dfrac{x}{\sqrt{x^2+1}}\,dx\).

We substitute \(x=\tan\theta\). Then \(dx=\sec^2\theta\,d\theta\) and so: \[\begin{aligned} \int \dfrac{x}{\sqrt{x^2+1}}\,dx &=\int \dfrac{\tan\theta}{\sqrt{\tan^2\theta+1}}\sec^2\theta\,d\theta =\int \dfrac{\tan\theta}{\sqrt{\sec^2\theta}}\sec^2\theta\,d\theta \\ &=\int \tan\theta\sec\theta\,d\theta=\sec\theta+C =\sqrt{x^2+1}+C \end{aligned}\] This solution was unnecessarily complicated. Always look for an ordinary substitution first:

Let \(u=x^2+1\). Then \(du=2x\,dx\) or \(\dfrac{1}{2}\,du=x\,dx\). So: \[ \int \dfrac{x}{\sqrt{x^2+1}}\,dx =\dfrac{1}{2}\int \dfrac{1}{\sqrt{u}}\,du =\sqrt{u}+C=\sqrt{x^2+1}+C \]

Now it's your turn:

Compute \(\displaystyle \int \dfrac{1}{(x^2+1)^{3/2}}\,dx\).

Let \(x=\tan\theta\).

\(\displaystyle \int \dfrac{1}{(x^2+1)^{3/2}}\,dx =\dfrac{x}{\sqrt{1+x^2}}+C\)

We substitute \(x=\tan\theta\). Then \(dx=\sec^2\theta\,d\theta\) and so: \[\begin{aligned} \int \dfrac{1}{(x^2+1)^{3/2}}\,dx &=\int \dfrac{1}{(\tan^2\theta+1)^{3/2}}\sec^2\theta\,d\theta \\ &=\int \dfrac{1}{\sec^3\theta}\sec^2\theta\,d\theta =\int \dfrac{1}{\sec\theta}\,d\theta \\ &=\int \cos\theta\,d\theta=\sin\theta+C \end{aligned}\] Examining the triangle, we see \(\sin\theta=\dfrac{\text{OPP}}{\text{HYP}}=\dfrac{x}{\sqrt{1+x^2}}\). So: \[ \int \dfrac{1}{(x^2+1)^{3/2}}\,dx =\dfrac{x}{\sqrt{1+x^2}}+C \]

We check by differentiating. If \(f(x)=\dfrac{x}{\sqrt{1+x^2}}\), then \[\begin{aligned} f'(x) &=\dfrac{\sqrt{1+x^2}(1)-x\dfrac{2x}{2\sqrt{1+x^2}}}{x^2+1} \\ &=\dfrac{(1+x^2)-x^2}{(x^2+1)^{3/2}} \\ &=\dfrac{1}{(x^2+1)^{3/2}} \end{aligned}\] which is the integrand we started with.

Compute \(\displaystyle \int_0^1 \dfrac{x^3}{(x^2+1)^{3/2}}\,dx\).

Use the ordinary substitution \(u=x^2+1\).

\(\displaystyle \int_0^1 \dfrac{x^3}{(x^2+1)^{3/2}}\,dx =\dfrac{3}{2}\sqrt{2}-2\)

We use the ordinary substitution \(u=x^2+1\). Then \(du=2x\,dx\) or \(\dfrac{1}{2}\,du=x\,dx\) and \(x^2=u-1\). Further, \[\begin{aligned} \text{If} \quad x=1 \quad & \text{then} \quad u=2. \\ \text{If} \quad x=0 \quad & \text{then} \quad u=1. \end{aligned}\] So: \[\begin{aligned} \int_0^1 \dfrac{x^3}{(x^2+1)^{3/2}}\,dx &=\dfrac{1}{2}\int_1^2 \dfrac{u-1}{u^{3/2}}\,du =\dfrac{1}{2}\int_1^2 (u^{-1/2}-u^{-3/2})\,du \\ &=\dfrac{1}{2}\left[\dfrac{}{}2u^{1/2}+2u^{-1/2}\right]_1^2 =\left[\dfrac{}{}u^{1/2}+u^{-1/2}\right]_1^2 \\ &=\left(\sqrt{2}+\dfrac{1}{\sqrt{2}}\right)-(1+1) =\dfrac{3}{2}\sqrt{2}-2 \end{aligned}\]

7. Trigonometric Substitutions

a1. Substitutions for \(x^2+1\) - Tangent Substitutions

Heading