7. Trigonometric Substitutions
c. Completing Squares
The trig substitutions of the previous pages can be generalized still further. If the integrand contains a quadratic polynomial \(Ax^2+Bx+C\) then you can complete the square and rewrite the polynomial as either: \[ a^2(x-p)^2+b^2 \qquad \text{or} \qquad a^2(x-p)^2-b^2 \]
How do I complete the square?
To complete the square on the quantity \(Ax^2+Bx+C\), means to rewrite it in the form \(A[(x-p)^2+q]\) or \(\pm a^2(x-p)^2\pm b^2\). To find \(p\) and \(q\), we equate the expressions, expand and equate coefficients: \[\begin{aligned} Ax^2+Bx+C&=A[(x-p)^2+q]=A[x^2-2px+p^2+q] \\ &=Ax^2-2Apx+Ap^2+Aq \end{aligned}\] Consequently, \(B=-2Ap\) and \(C=Ap^2+Aq\). Solving gives: \[\begin{aligned} p&=-\,\dfrac{B}{2A} \\ q&=\dfrac{C}{A}-p^2=\dfrac{C}{A}-\dfrac{B^2}{4A^2} \end{aligned}\] At the end, we can write \(A=\pm a^2\) and \(Aq=\pm b^2\).
Don't memorize this formulas! Memorize the process.In practice, we factor out the \(A\) and successively find \(p\) and then \(q\). For example: \[\begin{aligned} 4x^2-24x+20&=4(x^2-6x+5) \\ &=4(x^2-6x+9-4) \\ &=4[(x-3)^2-4] \\ &=2^2(x-3)^2-4^2 \end{aligned}\] To get the second and third lines, we looked at the coefficient of \(x\) which is \(-6=-2p\) to get \(p=3\). We square this to get the \(9\) and then identified \(q=-4\) to match the constant term \(5\).
In the former case, you can use a \(\tan\) substitution so that \(a(x-p)=b\tan\theta\). In the latter case, you can use a \(\sin\) or \(\sec\) substitution so that \(a(x-p)=b\sin\theta\) or \(a(x-p)=b\sec\theta\), depending on the size of \(|x-p|\). The \(\tan\) case is most common and most important:
Compute \(\displaystyle \int \dfrac{1}{x^2+6x+13}\,dx\).
We first complete the square: \[ x^2+6x+13=x^2+6x+9+4=(x+3)^2+4 \] Next we make the substitution \(x+3=2\tan\theta\). Then \(dx=2\sec^2\theta\,d\theta\) and: \[\begin{aligned} \int &\dfrac{1}{x^2+6x+13}\,dx =\int \dfrac{1}{(x+3)^2+4}\,dx \\ &=\int \dfrac{1}{4\tan^2\theta+4}2\sec^2\theta\,d\theta =\dfrac{1}{2}\int \dfrac{\sec^2\theta}{\sec^2\theta}\,d\theta \\ &=\dfrac{1}{2}\int 1\,d\theta =\dfrac{1}{2}\theta+C \end{aligned}\] To substitute back, we solve \(x+3=2\tan\theta\) for \(\theta=\arctan\dfrac{x+3}{2}\). Therefore \[ \int \dfrac{1}{x^2+6x+13}\,dx =\dfrac{1}{2}\arctan\dfrac{x+3}{2}+C \]
We check by differentiating. If \(f(x)=\dfrac{1}{2}\arctan\dfrac{x+3}{2}\), then: \[\begin{aligned} f'(x) &=\dfrac{1}{2}\dfrac{1}{1+\left(\dfrac{x+3}{2}\right)^2}\dfrac{1}{2} \\ &=\dfrac{1}{4+(x+3)^2}=\dfrac{1}{x^2+6x+13} \end{aligned}\] which is the integrand we started with.
Now it's your turn:
Compute \(\displaystyle \int \dfrac{1}{(4x-x^2)^{3/2}}\,dx\).
\[\begin{aligned} 4x-x^2&=-(x^2-4x) =-(x^2-4x+4-4) \\ &=-[(x-2)^2-4] =4-(x-2)^2 \end{aligned}\] Since this is inside of a \(\dfrac{3}{2}\) power, we let \(x-2=2\sin\theta\).
\(\displaystyle \int \dfrac{1}{(4x-x^2)^{3/2}}\,dx =\dfrac{1}{4}\dfrac{x-2}{\sqrt{4x-x^2}}+C\)
We first complete the square: \[\begin{aligned} 4x-x^2 &=-(x^2-4x)=-(x^2-4x+4-4) \\ &=-[(x-2)^2-4]=4-(x-2)^2 \end{aligned}\] Since this is inside of a \(\dfrac{3}{2}\) power, we let \(x-2=2\sin\theta\). Then \(dx=2\cos\theta\,d\theta\). The integral becomes: \[\begin{aligned} \int &\dfrac{1}{(4x-x^2)^{3/2}}\,dx =\int \dfrac{1}{[4-(x-2)^2]^{3/2}}\,dx \\ &=\int \dfrac{1}{[4-4\sin^2\theta]^{3/2}}2\cos\theta\,d\theta \\ &=\dfrac{1}{4}\int \dfrac{\cos\theta}{[1-\sin^2\theta]^{3/2}}\,d\theta =\dfrac{1}{4}\int \dfrac{\cos\theta}{\cos^3\theta}\,d\theta \\ &=\dfrac{1}{4}\int \sec^2\theta\,d\theta=\dfrac{1}{4}\tan\theta+C \end{aligned}\]
To substitute back, we know \(\sin\theta=\dfrac{x-2}{2}\). So we draw a right triangle with an angle \(\theta\) whose opposite side is \(x-2\) and whose hypotenuse is \(2\). These sides are chosen so that \(\sin\theta=\dfrac{x-2}{2}\). Then the adjacent side is \(\sqrt{4-(x-2)^2}\) and: \[ \tan\theta=\dfrac{x-2}{\sqrt{4-(x-2)^2}}=\dfrac{x-2}{\sqrt{4x-x^2}} \]
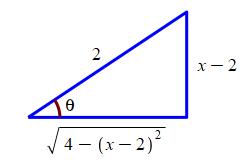
So the integral becomes: \[ \int \dfrac{1}{(4x-x^2)^{3/2}}\,dx =\dfrac{1}{4}\dfrac{x-2}{\sqrt{4x-x^2}}+C \]
We check by differentiating. If \(f(x)=\dfrac{1}{4}\dfrac{x-2}{\sqrt{4x-x^2}}\), then \[\begin{aligned} f'(x) &=\dfrac{1}{4}\dfrac{\sqrt{4x-x^2}(1)-(x-2)\dfrac{4-2x}{2\sqrt{4x-x^2}}}{4x-x^2} \\ &=\dfrac{1}{4}\dfrac{(4x-x^2)-(x-2)(2-x)}{(4x-x^2)^{3/2}} \\ &=\dfrac{1}{4}\dfrac{(4x-x^2)-(-x^2+4x-4)}{(4x-x^2)^{3/2}} \\ &=\dfrac{1}{(4x-x^2)^{3/2}} \end{aligned}\] which is the integrand we started with.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum