7. Trigonometric Substitutions

The trig substitutions of the previous three pages can be generalized to allow for coefficients.

b1. Substitutions for \(a^2x^2+b^2\)

Suppose we see an expression like \(9x^2+4\). This looks like \(x^2+1\) except that there are coefficients. So we still expect to do a \(\tan\) substitution, but slightly modified. We need to define our substitution so that \(9x^2=4\tan^2\theta\) because then \[ 9x^2+4=4\tan^2\theta+4=4(\tan^2\theta+1)=4\sec^2\theta \] Solving \(9x^2=4\tan^2\theta\) for \(x\) gives the substitution \(x=\dfrac{2}{3}\tan\theta\) and \(dx=\dfrac{2}{3}\sec^2\theta\,d\theta\). So it should still be possible to express the integrand in terms of \(\tan\theta\) and \(\sec\theta\) only.

Compute \(\displaystyle \int \dfrac{1}{\sqrt{9x^2+4}}\,dx\).

Let \(9x^2=4\tan^2\theta\) or \(x=\dfrac{2}{3}\tan\theta\). Then \(dx=\dfrac{2}{3}\sec^2\theta\,d\theta\) and so \[\begin{aligned} \int \dfrac{1}{\sqrt{9x^2+4}}\,dx &=\int \dfrac{1}{\sqrt{4\tan^2\theta+4}}\dfrac{2}{3}\sec^2\theta\,d\theta \\ &=\dfrac{1}{3}\int \dfrac{1}{\sqrt{\sec^2\theta}}\sec^2\theta\,d\theta =\dfrac{1}{3}\int \sec\theta\,d\theta \\ &=\dfrac{1}{3}\ln|\sec\theta+\tan\theta|+C \end{aligned}\]

To substitute back, we know \(\tan\theta=\dfrac{3x}{2}\). So: \[\begin{aligned} \sec\theta &=\sqrt{\tan^2\theta+1} =\sqrt{\dfrac{9x^2}{4}+1} \\ &=\dfrac{\sqrt{9x^2+4}}{2} \end{aligned}\] Or we can draw a right triangle with opposite side \(3x\) and adjacent side \(2\) so that \(\tan\theta=\dfrac{3x}{2}\). We conclude: \(\sec\theta=\dfrac{\sqrt{9x^2+4}}{2}\).

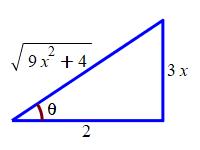
Then: \[\begin{aligned} \int \dfrac{1}{\sqrt{9x^2+4}}\,dx &=\dfrac{1}{3}\ln\left|\dfrac{\sqrt{9x^2+4}}{2}+\dfrac{3x}{2}\right|+C \\ &=\dfrac{1}{3}\ln\left|\sqrt{9x^2+4}+3x\right|-\dfrac{1}{3}\ln2+C \end{aligned}\]

We check by differentiating. If \(f(x)=\dfrac{1}{3}\ln\left|\sqrt{9x^2+4}+3x\right|\) then \[\begin{aligned} f'(x) &=\dfrac{1}{3}\dfrac{1}{\sqrt{9x^2+4}+3x} \left(\dfrac{9x}{\sqrt{9x^2+4}}+3\right) \\ &=\dfrac{1}{\sqrt{9x^2+4}+3x}\left(\dfrac{3x+\sqrt{9x^2+4}}{\sqrt{9x^2+4}}\right) =\dfrac{1}{\sqrt{9x^2+4}} \end{aligned}\] which is the integrand we started with.

If the integrand involves the quantity \(a^2x^2+b^2\) then it may be useful to make a substitution so that \(a^2x^2=b^2\tan^2\theta\). To do this, let \(x=\dfrac{b}{a}\tan\theta\). Then \(dx=\dfrac{b}{a}\sec^2\theta\,d\theta\) and:

\[\begin{aligned} a^2x^2+b^2 &=b^2\tan^2\theta+b^2=b^2(\tan^2\theta+1) \\ &=b^2\sec^2\theta \end{aligned}\] So it may be possible to re-express the integrand in terms of \(\tan\theta\) and \(\sec\theta\) only.

Compute \(\displaystyle \int \dfrac{1}{4x^2+9}\,dx\)

Let \(4x^2=9\tan^2\theta\).

\(\displaystyle \int \dfrac{1}{4x^2+9}\,dx =\dfrac{1}{6}\arctan\dfrac{2x}{3}+C\)

To make \(4x^2=9\tan^2\theta\), we substitute \(x=\dfrac{3}{2}\tan\theta\) and \(dx=\dfrac{3}{2}\sec^2\theta\,d\theta\). Then: \[\begin{aligned} \int \dfrac{1}{4x^2+9}\,dx &=\int \dfrac{1}{9\tan^2\theta+9}\,\dfrac{3}{2}\sec^2\theta\,d\theta \\ &=\dfrac{3}{9\cdot2}\int \dfrac{\sec^2\theta}{\tan^2\theta+1}\,d\theta \\ &=\dfrac{1}{6}\int 1\,d\theta=\dfrac{1}{6}\theta+C \end{aligned}\] To substitute back, we must solve \(x=\dfrac{3}{2}\tan\theta\) for \(\theta=\arctan\dfrac{2x}{3}\). Therefore: \[ \int \dfrac{1}{4x^2+9}\,dx =\dfrac{1}{6}\arctan\dfrac{2x}{3}+C \]

We check by differentiating. If \(f(x)=\dfrac{1}{6}\arctan \dfrac{2x}{3}\) then \[ f'(x) =\dfrac{1}{6}\dfrac{1}{\left(\dfrac{2x}{3}\right)^2+1}\dfrac{2}{3} =\dfrac{1}{4x^2+9} \] which is the integrand we started with.

You can also practice Trig Substitutions by using the following Maplet (requires Maple on the computer where this is executed):

Maplet: Trigonometric Substitutions Rate It

7. Trigonometric Substitutions

b1. Substitutions for \(a^2x^2+b^2\)

Heading