5. Vectors
b. Vector Addition
3. Properties
a. Triangle Inequality - Proof
Let \(\vec u\) and \(\vec v\) be arbitrary vectors. Then, \[ \left|\,|\vec u|-|\vec v|\,\right| \le |\vec u+\vec v| \le |\vec u|+|\vec v| \]
Proof
Consider a triangle with sides of lengths \(a\), \(b\) and \(c\). We will hold the lengths of \(a\) and \(b\) fixed while the angle between them changes. Then the length \(c\) changes.
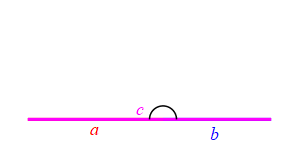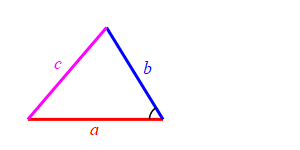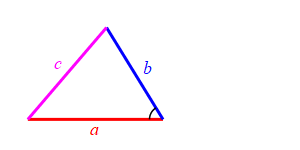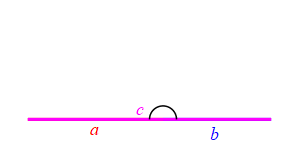
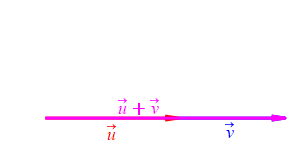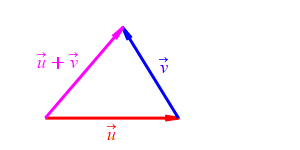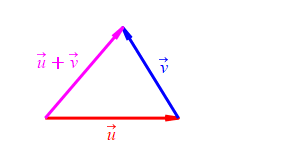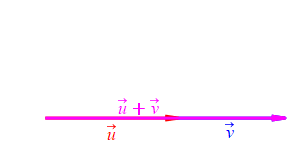
When the angle between sides \(a\) and \(b\) is very small, side \(c\) approaches \(|a-b|\) but always stays larger than this as long as the angle is non-zero. So: \[ c \ge |a-b| \]
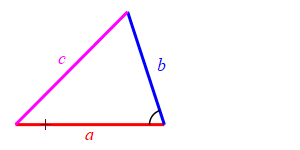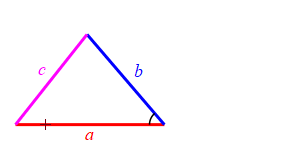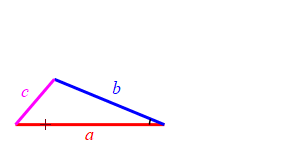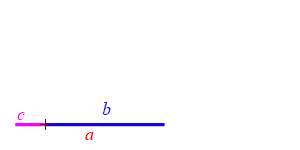
Because we don't know which is bigger, \(a\) or \(b\), and \(c\) must be bigger than the positive difference. The figure above has \(b \lt a\). The figure at the right has \(b \gt a\).
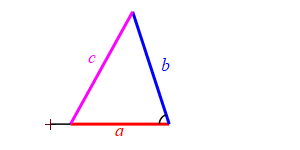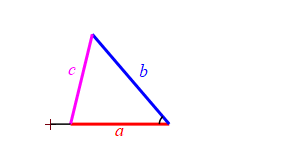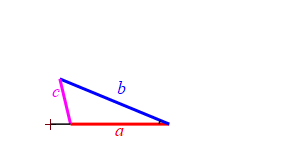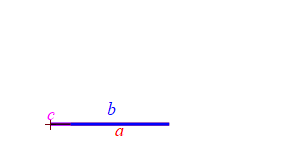
When the angle between sides \(a\) and \(b\) is very large, side \(c\) approaches \(a+b\) but always stays less than this as long as the angle is not \(180^\circ\). So: \[ c \le a+b \]
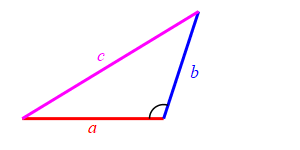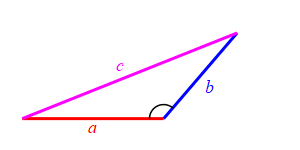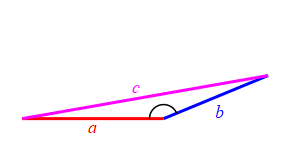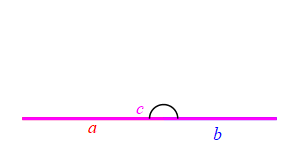
Together we have \[ |a-b| \le c \le a+b \]
Now let's use vectors. The lengths of the sides are \[ a=|\vec u| \qquad b=|\vec v| \qquad c=|\vec u+\vec v| \] So the inequalities become \[ \left|\,|\vec u|-|\vec v|\,\right| \le |\vec u+\vec v| \le |\vec u|+|\vec v| \] which is the triangle inequality.