5. Vectors
e. Parametric Curves
2. Intersections of Lines
In the plane, two (distinct) lines are either parallel or they intersect. We can tell when they are parallel, because their direction vectors will be proportional. If they are not parallel, then they intersect and we may be asked to find the point of intersection and/or the angle between the lines.
The angle between the lines is the angle between their tangent vectors. In finding the point of intersection remember that the parameter on each line may be different. This will become clear in the next example.
Consider the two straight lines \[\begin{aligned} L_1:\quad (x,y)&=(5-2t,2+t)\\ L_2:\quad (x,y)&=(2-t,1+3t) \end{aligned}\] Are they parallel or do they intersect? If they intersect, find the point of intersection and the angle between them.
The direction vectors are \[ \vec v_1=(-2,1) \qquad \text{and} \qquad \vec v_2=(-1,3) \] Since one is not a multiple of the other, the lines are not parallel; they intersect. The angle between them is the angle between their direction vectors: \[\begin{aligned} \cos\theta &=\dfrac{\vec v_1\cdot\vec v_2}{|\vec v_1|\,|\vec v_2|} =\dfrac{2+3}{\sqrt{5}\sqrt{10}} =\dfrac{1}{\sqrt{2}} \\ \theta &=\dfrac{\pi}{4}=45^\circ \end{aligned}\] We need to find the point of intersection.
Incorrect Attempt: One is first tempted to equate the \(x\) and \(y\) components of the two lines \(L_1\) and \(L_2\): \[\begin{aligned} 5-2t&=2-t \\ 2+t&=1+3t \end{aligned}\] Solving the first equation for \(t\), we get \(t=3\). Placing this value of \(t\) into the second equation, the left side is \(5\) while the right side is \(10\). This is impossible. It says there is no solution to this system of equations. This does not mean that the two lines do not intersect. Here's why: At the point of intersection, the parameter value for the first line may not be the same as the parameter value for the second line. Imagine having an ant crawling along each line. They each pass through the intersection point, but not at the same time.
Correct Method: To allow for the possibility that the parameter value may be different on the two lines, we change the parameter's name for the second line: \[\begin{aligned} L_1:\quad (x,y)&=(5-2t,2+t)\\ L_2:\quad (x,y)&=(2-s,1+3s) \end{aligned}\] What we really want is to solve the equation \(L_1(t)=L_2(s)\). We want to find a point \((x,y)\) which lies on \(L_1\) for some value of \(t\) and on \(L_2\) for some different value of \(s\).
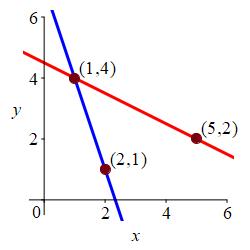
We equate the \(x\) and \(y\) components of the two lines: \[\begin{aligned} 5-2t&=2-s \\ 2+t&=1+3s \end{aligned}\] We add the first equation and twice the second to get \(9=4+5s\). Thus \(s=1\). Then the second equation gives \(2+t=4\) or \(t=2\). So the point of intersection is \(L_1(2)=(1,4)\).
To double check, we compute \(L_2(1)=(1,4)\) also.
Here is the plot.
Consider the two straight lines \[\begin{aligned} L_1:\quad (x,y)&=(-4+3t,8-2t)\\ L_2:\quad (x,y)&=(5+2t,15+3t) \end{aligned}\] Are they parallel or do they intersect? If they intersect, find the point of intersection and the angle between them.
They intersect at \(L_1(1)=L_2(-3)=(-1,6)\).
The lines are perpendicular.
The direction vectors are \(\vec v_1=\langle3,-2\rangle\) and \(\vec v_2=\langle2,3\rangle\). Since one is not a multiple of the other, the lines are not parallel; they intersect. So we need to find the point of intersection. To allow for the possibility that the parameter values may be different on the two lines, we change the parameter name for the second line: \[\begin{aligned} L_1(t):\quad (x,y)&=(-4+3t,8-2t)\\ L_2(s):\quad (x,y)&=(5+2s,15+3s) \end{aligned}\] and equate components: \[\begin{aligned} -4+3t&=5+2s \\ 8-2t&=15+3s \end{aligned}\] \(2\) times the first equation plus \(3\) times the second gives: \[ 16=55+13s \qquad \text{or} \qquad s=-3 \] Then the first equation gives: \[ -4+3t=5-6 \qquad \text{or} \qquad t=1 \] So the point of intersection is \(L_1(1)=(-1,6)\). To check, we compute \(L_2(-3)=(-1,6)\) also.
We compute the angle between them. Since \[ \vec v_1\cdot\vec v_2 =\langle3,-2\rangle\cdot\langle2,3\rangle=6-6=0 \] they are perpendicular.
You can also practice finding the intersetion of 2 lines in \(\mathbb{R}^2\) using the following Maplet (requires Maple on the computer where this is executed):
Intersection of 2 Lines in 2D in Slope-Intercept Form Rate It
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum