5. Vectors

d. Dot Product

3. Geometric Formula

To understand the meaning of the dot product, we turn to its geometric description in terms of the lengths of the vectors \(\vec u\) and \(\vec v\) and the angle \(\theta\) between them.

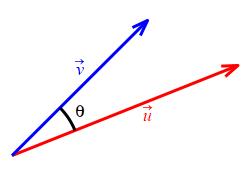
If \(\theta\) is the angle between two vectors \(\vec u\) and \(\vec v\), then their dot product is \[ \vec u\cdot\vec v=|\vec u|\,|\vec v|\cos\theta \] Memorize this! \(\quad\Longleftarrow\Longleftarrow\quad\) Read it! It's easy and informative.

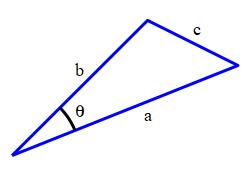
First recall the Law of Cosines which gives one side, \(c\), of a triangle in terms of the other two sides, \(a\) and \(b\), and the angle \(\theta\) between them.

\[ c^2=a^2+b^2-2ab\cos\theta \]

In order to compare the two diagrams above, we complete the vector picture into a triangle and note that the third side is \(\vec v-\vec u\) since by the tail to tip formula for vector addition: \[ \vec u+(\vec v-\vec u)=\vec v \]

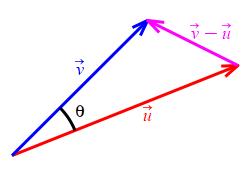
Comparing the figures, we have \[ a=|\vec u| \qquad \quad b=|\vec v| \qquad \quad c=|\vec v-\vec u| \] So the Law of Cosines says: \[ |\vec v-\vec u|^2=|\vec u|^2+|\vec v|^2-2|\vec u|\,|\vec v|\cos\theta \] However, there is another way to compute \(|\vec v-\vec u|^2\) using the properties of the dot product: \[\begin{aligned} |\vec v-\vec u|^2 &=(\vec v-\vec u)\cdot(\vec v-\vec u) &\quad&\text{Square Property}\\ &=\vec v\cdot\vec v-\vec v\cdot\vec u-\vec u\cdot\vec v+\vec u\cdot\vec u &\quad&\text{Distributive (FOIL)}\\ &=\vec v\cdot\vec v-2\vec u\cdot\vec v+\vec u\cdot\vec u &\quad&\text{Commutative}\\ &=|\vec u|^2+|\vec v|^2-2\vec u\cdot\vec v &\quad&\text{Square Property}\\ \end{aligned}\]

We now equate the two formulas for \(|\vec v-\vec u|^2\) and simplify \[\begin{aligned} |\vec u|^2+|\vec v|^2-2\vec u\cdot\vec v &=|\vec u|^2+|\vec v|^2-2|\vec u|\,|\vec v|\cos\theta \\ -2\vec u\cdot\vec v &=-2|\vec u|\,|\vec v|\cos\theta \\ \vec u\cdot\vec v &=|\vec u|\,|\vec v|\cos\theta \end{aligned}\] This is the geometric formula for dot product.

This formula is regarded as geometrical because it does not depend on the choice of coordinate axes. If we rotate the axes, the components of the individual vectors will change, but their lengths and the angle between them will not. It is not obvious that the algebraic formula for the dot product does not change. However, the geometric formula makes it clear that the dot product does not change.

Compute the dot product \(\vec a\cdot\vec b\) given that \(|\vec a|=3\) and \(|\vec b|=4\) and the angle between the two vectors is \(\theta=\dfrac{\pi}{4}\).

We use the geometric formula for the dot product: \[\begin{aligned} \vec a\cdot\vec b &=|\vec a|\,|\vec b|\cos\theta \\ &=3\cdot4\cdot\cos\dfrac{\pi}{4} =6\sqrt{2} \end{aligned}\]

Compute the dot product \(\vec c\cdot\vec d\) given that \(|\vec c|=1\) and \(|\vec d|=6\) and the angle between the two vectors is \(\theta=\dfrac{2\pi}{3}\).

\(\vec c\cdot\vec d=-3\)

\[\begin{aligned} \vec c\cdot\vec d&=|\vec c|\,|\vec d|\cos\theta \\ &=1\cdot6\cdot\cos\dfrac{2\pi}{3} =1\cdot6\cdot\dfrac{-1}{2}=-3 \end{aligned}\]

There is one further property of the dot product which follows from the geometric formula.

Let \(\vec u\) and \(\vec v\) be arbitrary non-zero vectors. Then,

Sign of the Dot Product:
1. The vectors \(\vec u\) and \(\vec v\) are or if and only if their dot product is zero: \[ \theta=\dfrac{\rule{0pt}{8pt}\pi}{\rule[-2pt]{0pt}{6pt}2}=90^\circ \quad \Longleftrightarrow \quad \vec u\cdot\vec v=0 \]
2. The angle between \(\vec u\) and \(\vec v\) is acute if and only if their dot product is positive: \[ \theta \lt \dfrac{\rule{0pt}{8pt}\pi}{\rule[-2pt]{0pt}{6pt}2}=90^\circ \quad \Longleftrightarrow \quad \vec u\cdot\vec v \gt 0 \]
3. The angle between \(\vec u\) and \(\vec v\) is obtuse if and only if their dot product is negative: \[ \theta \gt \dfrac{\rule{0pt}{8pt}\pi}{\rule[-2pt]{0pt}{6pt}2}=90^\circ \quad \Longleftrightarrow \quad \vec u\cdot\vec v \lt 0 \]

\(\quad\Longleftarrow\Longleftarrow\quad\) This is really easy.

Recall: \(\vec u\cdot\vec v=|\vec u|\,|\vec v|\cos\theta\)

If the vectors \(\vec u\) and \(\vec v\) are perpendicular, then \(\theta=\dfrac{\pi}{2}=90^\circ\) and \(\cos\theta=0\) so that \(\vec u\cdot\vec v=0\).
If the angle between \(\vec u\) and \(\vec v\) is acute, then \(\theta \lt \dfrac{\pi}{2}=90^\circ\) and \(\cos\theta \gt 0\) so that \(\vec u\cdot\vec v \gt 0\).
If the angle between \(\vec u\) and \(\vec v\) is obtuse, then \(\theta \gt \dfrac{\pi}{2}=90^\circ\) and \(\cos\theta \lt 0\) so that \(\vec u\cdot\vec v \lt 0\).

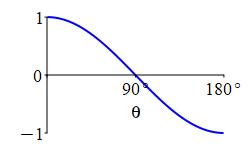
Since we assumed \(|\vec u| \ne 0\) and \(|\vec v| \ne 0\), these statements can be reversed, using \(\cos\theta=\dfrac{\vec u\cdot\vec v}{|\vec u|\,|\vec v|}\).

5. Vectors

d. Dot Product

3. Geometric Formula

Heading